
A | B | C | D | E | F | G | H | CH | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
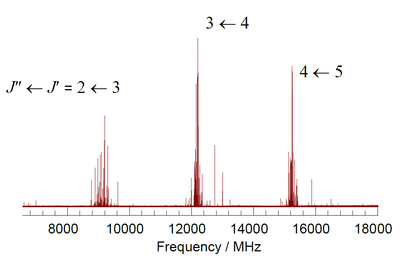
3I.[notes 1] Each rotational transition is labeled with the quantum numbers, J, of the final and initial states, and is extensively split by the effects of nuclear quadrupole coupling with the 127I nucleus.
Rotational spectroscopy is concerned with the measurement of the energies of transitions between quantized rotational states of molecules in the gas phase. The rotational spectrum (power spectral density vs. rotational frequency) of polar molecules can be measured in absorption or emission by microwave spectroscopy[1] or by far infrared spectroscopy. The rotational spectra of non-polar molecules cannot be observed by those methods, but can be observed and measured by Raman spectroscopy. Rotational spectroscopy is sometimes referred to as pure rotational spectroscopy to distinguish it from rotational-vibrational spectroscopy where changes in rotational energy occur together with changes in vibrational energy, and also from ro-vibronic spectroscopy (or just vibronic spectroscopy) where rotational, vibrational and electronic energy changes occur simultaneously.
For rotational spectroscopy, molecules are classified according to symmetry into spherical tops, linear molecules, and symmetric tops; analytical expressions can be derived for the rotational energy terms of these molecules. Analytical expressions can be derived for the fourth category, asymmetric top, for rotational levels up to J=3, but higher energy levels need to be determined using numerical methods. The rotational energies are derived theoretically by considering the molecules to be rigid rotors and then applying extra terms to account for centrifugal distortion, fine structure, hyperfine structure and Coriolis coupling. Fitting the spectra to the theoretical expressions gives numerical values of the angular moments of inertia from which very precise values of molecular bond lengths and angles can be derived in favorable cases. In the presence of an electrostatic field there is Stark splitting which allows molecular electric dipole moments to be determined.
An important application of rotational spectroscopy is in exploration of the chemical composition of the interstellar medium using radio telescopes.
Applications
Rotational spectroscopy has primarily been used to investigate fundamental aspects of molecular physics. It is a uniquely precise tool for the determination of molecular structure in gas-phase molecules. It can be used to establish barriers to internal rotation such as that associated with the rotation of the CH
3 group relative to the C
6H
4Cl group in chlorotoluene (C
7H
7Cl).[2] When fine or hyperfine structure can be observed, the technique also provides information on the electronic structures of molecules. Much of current understanding of the nature of weak molecular interactions such as van der Waals, hydrogen and halogen bonds has been established through rotational spectroscopy. In connection with radio astronomy, the technique has a key role in exploration of the chemical composition of the interstellar medium. Microwave transitions are measured in the laboratory and matched
to emissions from the interstellar medium using a radio telescope. NH
3 was the first stable polyatomic molecule to be identified in the interstellar medium.[3] The measurement of chlorine monoxide[4] is important for atmospheric chemistry. Current projects in astrochemistry involve both laboratory microwave spectroscopy and observations made using modern radiotelescopes such as the Atacama Large Millimeter/submillimeter Array (ALMA).[5]
Overview
A molecule in the gas phase is free to rotate relative to a set of mutually orthogonal axes of fixed orientation in space, centered on the center of mass of the molecule. Free rotation is not possible for molecules in liquid or solid phases due to the presence of intermolecular forces. Rotation about each unique axis is associated with a set of quantized energy levels dependent on the moment of inertia about that axis and a quantum number. Thus, for linear molecules the energy levels are described by a single moment of inertia and a single quantum number, , which defines the magnitude of the rotational angular momentum.
For nonlinear molecules which are symmetric rotors (or symmetric tops - see next section), there are two moments of inertia and the energy also depends on a second rotational quantum number, , which defines the vector component of rotational angular momentum along the principal symmetry axis.[6] Analysis of spectroscopic data with the expressions detailed below results in quantitative determination of the value(s) of the moment(s) of inertia. From these precise values of the molecular structure and dimensions may be obtained.
For a linear molecule, analysis of the rotational spectrum provides values for the rotational constant[notes 2] and the moment of inertia of the molecule, and, knowing the atomic masses, can be used to determine the bond length directly. For diatomic molecules this process is straightforward. For linear molecules with more than two atoms it is necessary to measure the spectra of two or more isotopologues, such as 16O12C32S and 16O12C34S. This allows a set of simultaneous equations to be set up and solved for the bond lengths).[notes 3] A bond length obtained in this way is slightly different from the equilibrium bond length. This is because there is zero-point energy in the vibrational ground state, to which the rotational states refer, whereas the equilibrium bond length is at the minimum in the potential energy curve. The relation between the rotational constants is given by
where v is a vibrational quantum number and α is a vibration-rotation interaction constant which can be calculated if the B values for two different vibrational states can be found.[7]
For other molecules, if the spectra can be resolved and individual transitions assigned both bond lengths and bond angles can be deduced. When this is not possible, as with most asymmetric tops, all that can be done is to fit the spectra to three moments of inertia calculated from an assumed molecular structure. By varying the molecular structure the fit can be improved, giving a qualitative estimate of the structure. Isotopic substitution is invaluable when using this approach to the determination of molecular structure.
Classification of molecular rotors
In quantum mechanics the free rotation of a molecule is quantized, so that the rotational energy and the angular momentum can take only certain fixed values, which are related simply to the moment of inertia, , of the molecule. For any molecule, there are three moments of inertia: , and about three mutually orthogonal axes A, B, and C with the origin at the center of mass of the system. The general convention, used in this article, is to define the axes such that , with axis corresponding to the smallest moment of inertia. Some authors, however, define the axis as the molecular rotation axis of highest order.
The particular pattern of energy levels (and, hence, of transitions in the rotational spectrum) for a molecule is determined by its symmetry. A convenient way to look at the molecules is to divide them into four different classes, based on the symmetry of their structure. These are
- Spherical tops (spherical rotors)
-
All three moments of inertia are equal to each other: . Examples of spherical tops include phosphorus tetramer (P
4), carbon tetrachloride (CCl
4) and other tetrahalides, methane (CH
4), silane, (SiH
4), sulfur hexafluoride (SF
6) and other hexahalides. The molecules all belong to the cubic point groups Td or Oh. - Linear molecules
-
For a linear molecule the moments of inertia are related by . For most purposes, can be taken to be zero. Examples of linear molecules include dioxygen (O
2), dinitrogen (N
2), carbon monoxide (CO), hydroxy radical (OH), carbon dioxide (CO2), hydrogen cyanide (HCN), carbonyl sulfide (OCS), acetylene (ethyne (HC≡CH) and dihaloethynes. These molecules belong to the point groups C∞v or D∞h. - Symmetric tops (symmetric rotors)
-
A symmetric top is a molecule in which two moments of inertia are the same, or . By definition a symmetric top must have a 3-fold or higher order rotation axis. As a matter of convenience, spectroscopists divide molecules into two classes of symmetric tops, Oblate symmetric tops (saucer or disc shaped) with and Prolate symmetric tops (rugby football, or cigar shaped) with . The spectra look rather different, and are instantly recognizable. Examples of symmetric tops include
- Oblate
- Benzene, C
6H
6; ammonia, NH
3; xenon tetrafluoride, XeF
4 - Prolate
- Chloromethane, CH
3Cl, propyne, CH
3C≡CH
- Asymmetric tops (asymmetric rotors)
-
The three moments of inertia have different values. Examples of small molecules that are asymmetric tops include water, H
2O and nitrogen dioxide, NO
2 whose symmetry axis of highest order is a 2-fold rotation axis. Most large molecules are asymmetric tops.
Selection rules
Microwave and far-infrared spectra
Transitions between rotational states can be observed in molecules with a permanent electric dipole moment.[9][notes 4] A consequence of this rule is that no microwave spectrum can be observed for centrosymmetric linear molecules such as N
2 (dinitrogen) or HCCH (ethyne), which are non-polar. Tetrahedral molecules such as CH
4 (methane), which have both a zero dipole moment and isotropic polarizability, would not have a pure rotation spectrum but for the effect of centrifugal distortion; when the molecule rotates about a 3-fold symmetry axis a small dipole moment is created, allowing a weak rotation spectrum to be observed by microwave spectroscopy.[10]
With symmetric tops, the selection rule for electric-dipole-allowed pure rotation transitions is ΔK = 0, ΔJ = ±1. Since these transitions are due to absorption (or emission) of a single photon with a spin of one, conservation of angular momentum implies that the molecular angular momentum can change by at most one unit.[11] Moreover, the quantum number K is limited to have values between and including +J to -J.[12]
Raman spectra
For Raman spectra the molecules undergo transitions in which an incident photon is absorbed and another scattered photon is emitted. The general selection rule for such a transition to be allowed is that the molecular polarizability must be anisotropic, which means that it is not the same in all directions.[13] Polarizability is a 3-dimensional tensor that can be represented as an ellipsoid. The polarizability ellipsoid of spherical top molecules is in fact spherical so those molecules show no rotational Raman spectrum. For all other molecules both Stokes and anti-Stokes lines[notes 5] can be observed and they have similar intensities due to the fact that many rotational states are thermally populated. The selection rule for linear molecules is ΔJ = 0, ±2. The reason for the values ±2 is that the polarizability returns to the same value twice during a rotation.[14] The value ΔJ = 0 does not correspond to a molecular transition but rather to Rayleigh scattering in which the incident photon merely changes direction.[15]
The selection rule for symmetric top molecules is
- ΔK = 0
- If K = 0, then ΔJ = ±2
- If K ≠ 0, then ΔJ = 0, ±1, ±2
Transitions with ΔJ = +1 are said to belong to the R series, whereas transitions with ΔJ = +2 belong to an S series.[15] Since Raman transitions involve two photons, it is possible for the molecular angular momentum to change by two units.
Units
The units used for rotational constants depend on the type of measurement. With infrared spectra in the wavenumber scale (), the unit is usually the inverse centimeter, written as cm−1, which is literally the number of waves in one centimeter, or the reciprocal of the wavelength in centimeters (). On the other hand, for microwave spectra in the frequency scale (), the unit is usually the gigahertz. The relationship between these two units is derived from the expression
where ν is a frequency, λ is a wavelength and c is the velocity of light. It follows that
Antropológia
Aplikované vedy
Bibliometria
Dejiny vedy
Encyklopédie
Filozofia vedy
Forenzné vedy
Humanitné vedy
Knižničná veda
Kryogenika
Kryptológia
Kulturológia
Literárna veda
Medzidisciplinárne oblasti
Metódy kvantitatívnej analýzy
Metavedy
Metodika
Text je dostupný za podmienok Creative
Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších
podmienok.
Podrobnejšie informácie nájdete na stránke Podmienky
použitia.
www.astronomia.sk | www.biologia.sk | www.botanika.sk | www.dejiny.sk | www.economy.sk | www.elektrotechnika.sk | www.estetika.sk | www.farmakologia.sk | www.filozofia.sk | Fyzika | www.futurologia.sk | www.genetika.sk | www.chemia.sk | www.lingvistika.sk | www.politologia.sk | www.psychologia.sk | www.sexuologia.sk | www.sociologia.sk | www.veda.sk I www.zoologia.sk



















