In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order.^[1][2][3] This concept first arose in calculus, and was later generalized to the more abstract setting of order theory.

In calculus and analysis

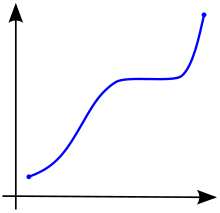
In calculus, a function ${\displaystyle f}$ defined on a subset of the real numbers with real values is called monotonic if and only if it is either entirely non-increasing, or entirely non-decreasing.^[2] That is, as per Fig. 1, a function that increases monotonically does not exclusively have to increase, it simply must not decrease.

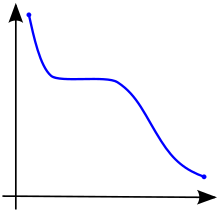
A function is called monotonically increasing (also increasing or non-decreasing)^[3] if for all ${\displaystyle x}$ and ${\displaystyle y}$ such that ${\displaystyle x\leq y}$ one has ${\displaystyle f\!\left(x\right)\leq f\!\left(y\right)}$, so ${\displaystyle f}$ preserves the order (see Figure 1). Likewise, a function is called monotonically decreasing (also decreasing or non-increasing)^[3] if, whenever ${\displaystyle x\leq y}$, then ${\displaystyle f\!\left(x\right)\geq f\!\left(y\right)}$, so it reverses the order (see Figure 2).

If the order ${\displaystyle \leq }$ in the definition of monotonicity is replaced by the strict order ${\displaystyle <}$, one obtains a stronger requirement. A function with this property is called strictly increasing (also increasing).^[3][4] Again, by inverting the order symbol, one finds a corresponding concept called strictly decreasing (also decreasing).^[3][4] A function with either property is called strictly monotone. Functions that are strictly monotone are one-to-one (because for ${\displaystyle x}$ not equal to ${\displaystyle y}$, either ${\displaystyle x<y}$ or ${\displaystyle x>y}$ and so, by monotonicity, either ${\displaystyle f\!\left(x\right)<f\!\left(y\right)}$ or ${\displaystyle f\!\left(x\right)>f\!\left(y\right)}$, thus ${\displaystyle f\!\left(x\right)\neq f\!\left(y\right)}$.)

To avoid ambiguity, the terms weakly monotone, weakly increasing and weakly decreasing are often used to refer to non-strict monotonicity.

The terms "non-decreasing" and "non-increasing" should not be confused with the (much weaker) negative qualifications "not decreasing" and "not increasing". For example, the non-monotonic function shown in figure 3 first falls, then rises, then falls again. It is therefore not decreasing and not increasing, but it is neither non-decreasing nor non-increasing.

A function ${\displaystyle f}$ is said to be absolutely monotonic over an interval ${\displaystyle \left(a,b\right)}$ if the derivatives of all orders of ${\displaystyle f}$ are nonnegative or all nonpositive at all points on the interval.

Inverse of function

All strictly monotonic functions are invertible because they are guaranteed to have a one-to-one mapping from their range to their domain.

However, functions that are only weakly monotone are not invertible because they are constant on some interval (and therefore are not one-to-one).

A function may be strictly monotonic over a limited a range of values and thus have an inverse on that range even though it is not strictly monotonic everywhere. For example, if ${\displaystyle y=g(x)}$ is strictly increasing on the range ${\displaystyle }$, then it has an inverse ${\displaystyle x=h(y)}$ on the range ${\displaystyle }$.

The term monotonic is sometimes used in place of strictly monotonic, so a source may state that all monotonic functions are invertible when they really mean that all strictly monotonic functions are invertible.^{[citation needed]}

Monotonic transformation

The term monotonic transformation (or monotone transformation) may also cause confusion because it refers to a transformation by a strictly increasing function. This is the case in economics with respect to the ordinal properties of a utility function being preserved across a monotonic transform (see also monotone preferences).^[5] In this context, the term "monotonic transformation" refers to a positive monotonic transformation and is intended to distinguish it from a "negative monotonic transformation," which reverses the order of the numbers.^[6]

Some basic applications and results

The following properties are true for a monotonic function ${\displaystyle f\colon \mathbb {R} \to \mathbb {R} }$:

• ${\displaystyle f}$ has limits from the right and from the left at every point of its domain;
• ${\displaystyle f}$ has a limit at positive or negative infinity (${\displaystyle \pm \infty }$) of either a real number, ${\displaystyle \infty }$, or ${\displaystyle -\infty }$.
• ${\displaystyle f}$ can only have jump discontinuities;
• ${\displaystyle f}$ can only have countably many discontinuities in its domain. The discontinuities, however, do not necessarily consist of isolated points and may even be dense in an interval (a, b). For example, for any summable sequence $(a_{i})$ of positive numbers and any enumeration ${\displaystyle (q_{i})}$ of the rational numbers, the monotonically increasing function
  $${\displaystyle f(x)=\sum _{q_{i}\leq x}a_{i}}$$

  
  is continuous exactly at every irrational number (cf. picture). It is the cumulative distribution function of the discrete measure on the rational numbers, where ${\displaystyle a_{i}}$ is the weight of ${\displaystyle q_{i}}$.

These properties are the reason why monotonic functions are useful in technical work in analysis. Other important properties of these functions include:

• if ${\displaystyle f}$ is a monotonic function defined on an interval ${\displaystyle I}$, then ${\displaystyle f}$ is differentiable almost everywhere on ${\displaystyle I}$; i.e. the set of numbers ${\displaystyle x}$ in ${\displaystyle I}$ such that ${\displaystyle f}$ is not differentiable in ${\displaystyle x}$ has Lebesgue measure zero. In addition, this result cannot be improved to countable: see Cantor function.
• if this set is countable, then ${\displaystyle f}$ is absolutely continuous
• if ${\displaystyle f}$ is a monotonic function defined on an interval ${\displaystyle \left}$, then ${\displaystyle f}$ is Riemann integrable.

An important application of monotonic functions is in probability theory. If ${\displaystyle X}$ is a random variable, its cumulative distribution function ${\displaystyle F_{X}\!\left(x\right)={\text{Prob}}\!\left(X\leq x\right)}$ is a monotonically increasing function.

A function is unimodal if it is monotonically increasing up to some point (the mode) and then monotonically decreasing.

When ${\displaystyle f}$ is a strictly monotonic function, then ${\displaystyle f}$ is injective on its domain, and if ${\displaystyle T}$ is the range of ${\displaystyle f}$, then there is an inverse function on ${\displaystyle T}$ for ${\displaystyle f}$. In contrast, each constant function is monotonic, but not injective,^[7] and hence cannot have an inverse.

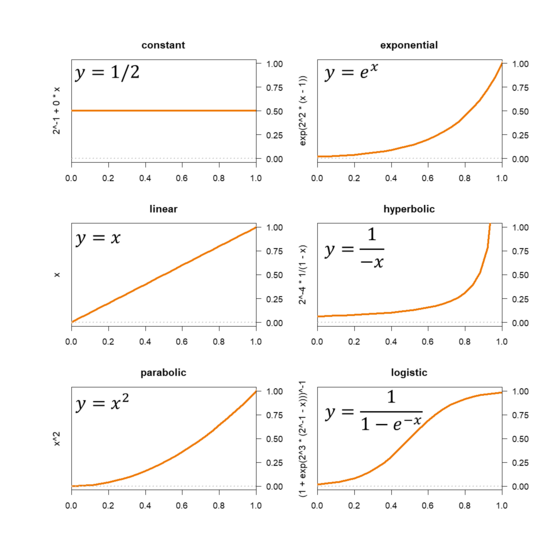
The graphic shows six monotonic functions. Their simplest forms are shown in the plot area and the expressions used to create them are shown on the y-axis.

In topology

A map ${\displaystyle f:}$Zdroj:https://en.wikipedia.org?pojem=Monotonic
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.