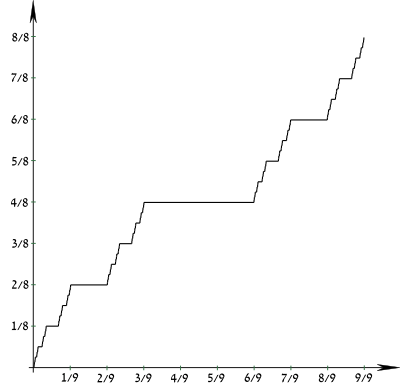
In mathematics, the Cantor function is an example of a function that is continuous, but not absolutely continuous. It is a notorious counterexample in analysis, because it challenges naive intuitions about continuity, derivative, and measure. Though it is continuous everywhere and has zero derivative almost everywhere, its value still goes from 0 to 1 as its argument reaches from 0 to 1. Thus, in one sense the function seems very much like a constant one which cannot grow, and in another, it does indeed monotonically grow.

It is also called the Cantor ternary function, the Lebesgue function,^[1] Lebesgue's singular function, the Cantor–Vitali function, the Devil's staircase,^[2] the Cantor staircase function,^[3] and the Cantor–Lebesgue function.^[4] Georg Cantor (1884) introduced the Cantor function and mentioned that Scheeffer pointed out that it was a counterexample to an extension of the fundamental theorem of calculus claimed by Harnack. The Cantor function was discussed and popularized by Scheeffer (1884), Lebesgue (1904) and Vitali (1905).

Definition

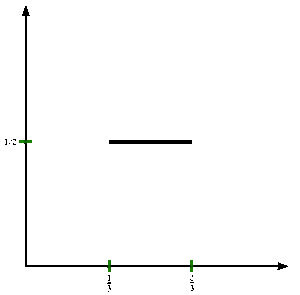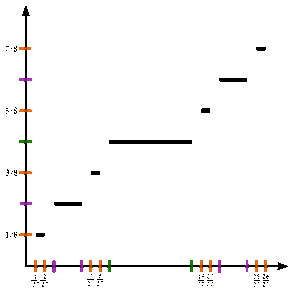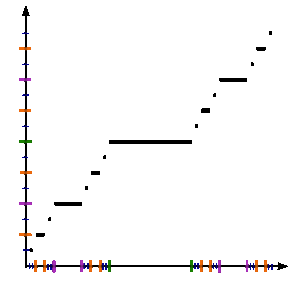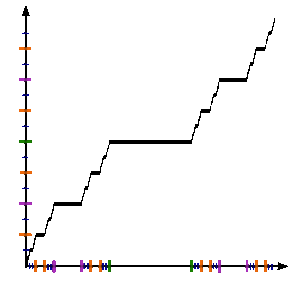
To define the Cantor function ${\displaystyle c:\to }$, let ${\displaystyle x}$ be any number in ${\displaystyle }$ and obtain ${\displaystyle c(x)}$ by the following steps:

1. Express ${\displaystyle x}$ in base 3, using digits 0, 1, 2.
2. If the base-3 representation of ${\displaystyle x}$ contains a 1, replace every digit strictly after the first 1 with 0.
3. Replace any remaining 2s with 1s.
4. Interpret the result as a binary number. The result is ${\displaystyle c(x)}$.

For example:

• ${\displaystyle {\tfrac {1}{4}}}$ has the ternary representation 0.02020202... There are no 1s so the next stage is still 0.02020202... This is rewritten as 0.01010101... This is the binary representation of ${\displaystyle {\tfrac {1}{3}}}$, so ${\displaystyle c({\tfrac {1}{4}})={\tfrac {1}{3}}}$.
• ${\displaystyle {\tfrac {1}{5}}}$ has the ternary representation 0.01210121... The digits after the first 1 are replaced by 0s to produce 0.01000000... This is not rewritten since it has no 2s. This is the binary representation of ${\displaystyle {\tfrac {1}{4}}}$, so ${\displaystyle c({\tfrac {1}{5}})={\tfrac {1}{4}}}$.
• ${\displaystyle {\tfrac {200}{243}}}$ has the ternary representation 0.21102 (or 0.211012222...). The digits after the first 1 are replaced by 0s to produce 0.21. This is rewritten as 0.11. This is the binary representation of ${\displaystyle {\tfrac {3}{4}}}$, so ${\displaystyle c({\tfrac {200}{243}})={\tfrac {3}{4}}}$.

Equivalently, if ${\displaystyle {\mathcal {C}}}$ is the Cantor set on , then the Cantor function ${\displaystyle c:\to }$ can be defined as

${\displaystyle c(x)={\begin{cases}\sum _{n=1}^{\infty }{\frac {a_{n}}{2^{n}}},&x=\sum _{n=1}^{\infty }{\frac {2a_{n}}{3^{n}}}\in {\mathcal {C}}\ \mathrm {for} \ a_{n}\in \{0,1\};\\\sup _{y\leq x,\,y\in {\mathcal {C}}}c(y),&x\in 0,1\smallsetminus {\mathcal {C}}.\end{cases}}}$

This formula is well-defined, since every member of the Cantor set has a unique base 3 representation that only contains the digits 0 or 2. (For some members of ${\displaystyle {\mathcal {C}}}$, the ternary expansion is repeating with trailing 2's and there is an alternative non-repeating expansion ending in 1. For example, ${\displaystyle {\tfrac {1}{3}}}$ = 0.1₃ = 0.02222...₃ is a member of the Cantor set). Since ${\displaystyle c(0)=0}$ and ${\displaystyle c(1)=1}$, and ${\displaystyle c}$ is monotonic on ${\displaystyle {\mathcal {C}}}$, it is clear that ${\displaystyle 0\leq c(x)\leq 1}$ also holds for all ${\displaystyle x\in 0,1\smallsetminus {\mathcal {C}}}$.

Propertiesedit

The Cantor function challenges naive intuitions about continuity and measure; though it is continuous everywhere and has zero derivative almost everywhere, ${\textstyle c(x)}$ goes from 0 to 1 as ${\textstyle x}$ goes from 0 to 1, and takes on every value in between. The Cantor function is the most frequently cited example of a real function that is uniformly continuous (precisely, it is Hölder continuous of exponent α = log 2/log 3) but not absolutely continuous. It is constant on intervals of the form (0.x₁x₂x₃...x_n022222..., 0.x₁x₂x₃...x_n200000...), and every point not in the Cantor set is in one of these intervals, so its derivative is 0 outside of the Cantor set. On the other hand, it has no derivative at any point in an uncountable subset of the Cantor set containing the interval endpoints described above.

The Cantor function can also be seen as the cumulative probability distribution function of the 1/2-1/2 Bernoulli measure μ supported on the Cantor set: ${\textstyle c(x)=\mu (0,x)}$. This probability distribution, called the Cantor distribution, has no discrete part. That is, the corresponding measure is atomless. This is why there are no jump discontinuities in the function; any such jump would correspond to an atom in the measure.

However, no non-constant part of the Cantor function can be represented as an integral of a probability density function; integrating any putative probability density function that is not almost everywhere zero over any interval will give positive probability to some interval to which this distribution assigns probability zero. In particular, as Vitali (1905) pointed out, the function is not the integral of its derivative even though the derivative exists almost everywhere.

The Cantor function is the standard example of a singular function.

The Cantor function is also a standard example of a function with bounded variation but, as mentioned above, is not absolutely continuous. However, every absolutely continuous function is continuous with bounded variation.

The Cantor function is non-decreasing, and so in particular its graph defines a rectifiable curve. Scheeffer (1884) showed that the arc length of its graph is 2. Note that the graph of any nondecreasing function such that ${\displaystyle f(0)=0}$ and ${\displaystyle f(1)=1}$ has length not greater than 2. In this sense, the Cantor function is extremal.

Lack of absolute continuityedit

Because the Lebesgue measure of the uncountably infinite Cantor set is 0, for any positive ε < 1 and δ, there exists a finite sequence of pairwise disjoint sub-intervals with total length < δ over which the Cantor function cumulatively rises more than ε.

In fact, for every δ > 0 there are finitely many pairwise disjoint intervals (x_k,y_k) (1 ≤ k ≤ M) with ${\displaystyle \sum \limits _{k=1}^{M}(y_{k}-x_{k})<\delta }$ and ${\displaystyle \underset{k=1}{\overset{M}{\sum <!--\; \sum \; -->}}(c({}_{}}$Zdroj:https://en.wikipedia.org?pojem=Cantor_function
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.