In measure theory, a branch of mathematics, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of higher dimensional Euclidean n-spaces. For lower dimensions n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called n-dimensional volume, n-volume, hypervolume, or simply volume.^[1] It is used throughout real analysis, in particular to define Lebesgue integration. Sets that can be assigned a Lebesgue measure are called Lebesgue-measurable; the measure of the Lebesgue-measurable set A is here denoted by λ(A).

Henri Lebesgue described this measure in the year 1901 which, a year after, was followed up by his description of the Lebesgue integral. Both were published as part of his dissertation in 1902.^[2]

Definition

For any interval ${\displaystyle I=}$, or ${\displaystyle I=(a,b)}$, in the set ${\displaystyle \mathbb {R} }$ of real numbers, let ${\displaystyle \ell (I)=b-a}$ denote its length. For any subset ${\displaystyle E\subseteq \mathbb {R} }$, the Lebesgue outer measure^[3] ${\displaystyle \lambda ^{\!*\!}(E)}$ is defined as an infimum

${\displaystyle \lambda ^{\!*\!}(E)=\inf \left\{\sum _{k=1}^{\infty }\ell (I_{k}):{(I_{k})_{k\in \mathbb {N} }}{\text{ is a sequence of open intervals with }}E\subset \bigcup _{k=1}^{\infty }I_{k}\right\}.}$

The above definition can be generalised to higher dimensions as follows.^[4] For any rectangular cuboid ${\displaystyle C}$ which is a Cartesian product ${\displaystyle C=I_{1}\times \cdots \times I_{n}}$ of open intervals, let ${\displaystyle \operatorname {vol} (C)=\ell (I_{1})\times \cdots \times \ell (I_{n})}$ (a real number product) denote its volume. For any subset ${\displaystyle E\subseteq \mathbb {R^{n}} }$,

${\displaystyle \lambda ^{\!*\!}(E)=\inf \left\{\sum _{k=1}^{\infty }\operatorname {vol} (C_{k}):{(C_{k})_{k\in \mathbb {N} }}{\text{ is a sequence of products of open intervals with }}E\subset \bigcup _{k=1}^{\infty }C_{k}\right\}.}$

Some sets ${\displaystyle E}$ satisfy the Carathéodory criterion, which requires that for every ${\displaystyle A\subseteq \mathbb {R} }$,

${\displaystyle \lambda ^{\!*\!}(A)=\lambda ^{\!*\!}(A\cap E)+\lambda ^{\!*\!}(A\cap E^{c}).}$

The sets ${\displaystyle E}$ that satisfy the Carathéodory criterion are said to be Lebesgue-measurable, with its Lebesgue measure being defined as its Lebesgue outer measure: ${\displaystyle \lambda (E)=\lambda ^{\!*\!}(E)}$. The set of all such ${\displaystyle E}$ forms a σ-algebra.

A set ${\displaystyle E}$ that does not satisfy the Carathéodory criterion is not Lebesgue-measurable. ZFC proves that non-measurable sets do exist; an example is the Vitali sets.

Intuition

The first part of the definition states that the subset ${\displaystyle E}$ of the real numbers is reduced to its outer measure by coverage by sets of open intervals. Each of these sets of intervals ${\displaystyle I}$ covers ${\displaystyle E}$ in a sense, since the union of these intervals contains ${\displaystyle E}$. The total length of any covering interval set may overestimate the measure of ${\displaystyle E,}$ because ${\displaystyle E}$ is a subset of the union of the intervals, and so the intervals may include points which are not in ${\displaystyle E}$. The Lebesgue outer measure emerges as the greatest lower bound (infimum) of the lengths from among all possible such sets. Intuitively, it is the total length of those interval sets which fit ${\displaystyle E}$ most tightly and do not overlap.

That characterizes the Lebesgue outer measure. Whether this outer measure translates to the Lebesgue measure proper depends on an additional condition. This condition is tested by taking subsets ${\displaystyle A}$ of the real numbers using ${\displaystyle E}$ as an instrument to split ${\displaystyle A}$ into two partitions: the part of ${\displaystyle A}$ which intersects with ${\displaystyle E}$ and the remaining part of ${\displaystyle A}$ which is not in ${\displaystyle E}$: the set difference of ${\displaystyle A}$ and ${\displaystyle E}$. These partitions of ${\displaystyle A}$ are subject to the outer measure. If for all possible such subsets ${\displaystyle A}$ of the real numbers, the partitions of ${\displaystyle A}$ cut apart by ${\displaystyle E}$ have outer measures whose sum is the outer measure of ${\displaystyle A}$, then the outer Lebesgue measure of ${\displaystyle E}$ gives its Lebesgue measure. Intuitively, this condition means that the set ${\displaystyle E}$ must not have some curious properties which causes a discrepancy in the measure of another set when ${\displaystyle E}$ is used as a "mask" to "clip" that set, hinting at the existence of sets for which the Lebesgue outer measure does not give the Lebesgue measure. (Such sets are, in fact, not Lebesgue-measurable.)

Examples

• Any closed interval of real numbers is Lebesgue-measurable, and its Lebesgue measure is the length b − a. The open interval (a, b) has the same measure, since the difference between the two sets consists only of the end points a and b, which each have measure zero.
• Any Cartesian product of intervals and is Lebesgue-measurable, and its Lebesgue measure is (b − a)(d − c), the area of the corresponding rectangle.
• Moreover, every Borel set is Lebesgue-measurable. However, there are Lebesgue-measurable sets which are not Borel sets.^[5][6]
• Any countable set of real numbers has Lebesgue measure 0. In particular, the Lebesgue measure of the set of algebraic numbers is 0, even though the set is dense in ${\displaystyle \mathbb {R} }$.
• The Cantor set and the set of Liouville numbers are examples of uncountable sets that have Lebesgue measure 0.
• If the axiom of determinacy holds then all sets of reals are Lebesgue-measurable. Determinacy is however not compatible with the axiom of choice.
• Vitali sets are examples of sets that are not measurable with respect to the Lebesgue measure. Their existence relies on the axiom of choice.
• Osgood curves are simple plane curves with positive Lebesgue measure^[7] (it can be obtained by small variation of the Peano curve construction). The dragon curve is another unusual example.
• Any line in ${\displaystyle \mathbb {R} ^{n}}$, for ${\displaystyle n\geq 2}$, has a zero Lebesgue measure. In general, every proper hyperplane has a zero Lebesgue measure in its ambient space.
• The volume of an n-ball can be calculated in terms of Euler's gamma function.

Properties

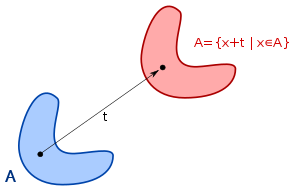
The Lebesgue measure on Rⁿ has the following properties:

1. If A is a cartesian product of intervals I₁ × I₂ × ⋯ × I_n, then A is Lebesgue-measurable and ${\displaystyle \mathrm{\lambda <!--\; \lambda \; -->}(A}$Zdroj:https://en.wikipedia.org?pojem=Lebesgue_measure
   Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

   ---