Part of a series on
Spacetime
Special relativity General relativity
Spacetime concepts Spacetime manifold Equivalence principle Lorentz transformations Minkowski space
General relativity Introduction to general relativity Mathematics of general relativity Einstein field equations
Classical gravity Introduction to gravitation Newton's law of universal gravitation
Relevant mathematics Four-vector Derivations of relativity Spacetime diagrams Differential geometry Curved spacetime Mathematics of general relativity Spacetime topology
Physics portal  Category
v t e

A spacetime diagram is a graphical illustration of locations in space at various times, especially in the special theory of relativity. Spacetime diagrams can show the geometry underlying phenomena like time dilation and length contraction without mathematical equations.

The history of an object's location through time traces out a line or curve on a spacetime diagram, referred to as the object's world line. Each point in a spacetime diagram represents a unique position in space and time and is referred to as an event.

The most well-known class of spacetime diagrams are known as Minkowski diagrams, developed by Hermann Minkowski in 1908. Minkowski diagrams are two-dimensional graphs that depict events as happening in a universe consisting of one space dimension and one time dimension. Unlike a regular distance-time graph, the distance is displayed on the horizontal axis and time on the vertical axis. Additionally, the time and space units of measurement are chosen in such a way that an object moving at the speed of light is depicted as following a 45° angle to the diagram's axes.

Introduction to kinetic diagrams

Position versus time graphs

In the study of 1-dimensional kinematics, position vs. time graphs (called x-t graphs for short) provide a useful means to describe motion. Kinematic features besides the object's position are visible by the slope and shape of the lines.^[1] In Fig 1-1, the plotted object moves away from the origin at a positive constant velocity (1.66 m/s) for 6 seconds, halts for 5 seconds, then returns to the origin over a period of 7 seconds at a non-constant speed (but negative velocity).

At its most basic level, a spacetime diagram is merely a time vs position graph, with the directions of the axes in a usual p-t graph exchanged; that is, the vertical axis refers to temporal and the horizontal axis to spatial coordinate values. Especially when used in special relativity (SR), the temporal axes of a spacetime diagram are often scaled with the speed of light c, and thus are often labeled by ct. This changes the dimension of the addressed physical quantity from <Time> to <Length>, in accordance with the dimension associated with the spatial axis, which is frequently labeled x.

Standard configuration of reference frames

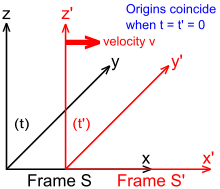
To ease insight into how spacetime coordinates, measured by observers in different reference frames, compare with each other, it is useful to standardize and simplify the setup. Two Galilean reference frames (i.e., conventional 3-space frames), S and S′ (pronounced "S prime"), each with observers O and O′ at rest in their respective frames, but measuring the other as moving with speeds ±v are said to be in standard configuration, when:

• The x, y, z axes of frame S are oriented parallel to the respective primed axes of frame S′.
• The origins of frames S and S′ coincide at time t = 0 in frame S and also at t′ = 0 in frame S′.^[2]: 107
• Frame S′ moves in the x-direction of frame S with velocity v as measured in frame S.

This spatial setting is displayed in the Fig 1-2, in which the temporal coordinates are separately annotated as quantities t and t'.

In a further step of simplification it is often sufficient to consider just the direction of the observed motion and ignore the other two spatial components, allowing x and ct to be plotted in 2-dimensional spacetime diagrams, as introduced above.

Non-relativistic "spacetime diagrams"

The black axes labelled x and ct on Fig 1-3 are the coordinate system of an observer, referred to as at rest, and who is positioned at x = 0. This observer's world line is identical with the ct time axis. Each parallel line to this axis would correspond also to an object at rest but at another position. The blue line describes an object moving with constant speed v to the right, such as a moving observer.

This blue line labelled ct′ may be interpreted as the time axis for the second observer. Together with the x axis, which is identical for both observers, it represents their coordinate system. Since the reference frames are in standard configuration, both observers agree on the location of the origin of their coordinate systems. The axes for the moving observer are not perpendicular to each other and the scale on their time axis is stretched. To determine the coordinates of a certain event, two lines, each parallel to one of the two axes, must be constructed passing through the event, and their intersections with the axes read off.

Determining position and time of the event A as an example in the diagram leads to the same time for both observers, as expected. Only for the position different values result, because the moving observer has approached the position of the event A since t = 0. Generally stated, all events on a line parallel to the x axis happen simultaneously for both observers. There is only one universal time t = t′, modelling the existence of one common position axis. On the other hand, due to two different time axes the observers usually measure different coordinates for the same event. This graphical translation from x and t to x′ and t′ and vice versa is described mathematically by the so-called Galilean transformation.

Minkowski diagrams

Overview

The term Minkowski diagram refers to a specific form of spacetime diagram frequently used in special relativity. A Minkowski diagram is a two-dimensional graphical depiction of a portion of Minkowski space, usually where space has been curtailed to a single dimension. The units of measurement in these diagrams are taken such that the light cone at an event consists of the lines of slope plus or minus one through that event.^[3] The horizontal lines correspond to the usual notion of simultaneous events for a stationary observer at the origin.

A particular Minkowski diagram illustrates the result of a Lorentz transformation. The Lorentz transformation relates two inertial frames of reference, where an observer stationary at the event (0, 0) makes a change of velocity along the x-axis. As shown in Fig 2-1, the new time axis of the observer forms an angle α with the previous time axis, with α < π/4. In the new frame of reference the simultaneous events lie parallel to a line inclined by α to the previous lines of simultaneity. This is the new x-axis. Both the original set of axes and the primed set of axes have the property that they are orthogonal with respect to the Minkowski inner product or relativistic dot product.

Whatever the magnitude of α, the line ct = x forms the universal^[4] bisector, as shown in Fig 2-2.

One frequently encounters Minkowski diagrams where the time units of measurement are scaled by a factor of c such that one unit of x equals one unit of t. Such a diagram may have units of

• Approximately 30 centimetres length and nanoseconds
• Astronomical units and intervals of about 8 minutes and 19 seconds (499 seconds)
• Light years and years
• Light-second and second

With that, light paths are represented by lines parallel to the bisector between the axes.

Mathematical details

The angle α between the x and x′ axes will be identical with that between the time axes ct and ct′. This follows from the second postulate of special relativity, which says that the speed of light is the same for all observers, regardless of their relative motion (see below). The angle α is given by^[5]

${\displaystyle \tan \alpha ={\frac {v}{c}}=\beta .}$

The corresponding boost from x and t to x′ and t′ and vice versa is described mathematically by the Lorentz transformation, which can be written

${\displaystyle {\begin{aligned}ct'&=\gamma (ct-\beta x),\\x'&=\gamma (x-\beta ct)\\\end{aligned}}}$

where ${\textstyle \gamma =\left(1-\beta ^{2}\right)^{-{\frac {1}{2}}}}$ is the Lorentz factor. By applying the Lorentz transformation, the spacetime axes obtained for a boosted frame will always correspond to conjugate diameters of a pair of hyperbolas.

As illustrated in Fig 2-3, the boosted and unboosted spacetime axes will in general have unequal unit lengths. If U is the unit length on the axes of ct and x respectively, the unit length on the axes of ct′ and x′ is:^[6]

${\displaystyle U'=U{\sqrt {\frac {1+\beta ^{2}}{1-\beta ^{2}}}}\,.}$

The ct-axis represents the worldline of a clock resting in S, with U representing the duration between two events happening on this worldline, also called the proper time between these events. Length U upon the x-axis represents the rest length or proper length of a rod resting in S. The same interpretation can also be applied to distance U′ upon the ct′- and x′-axes for clocks and rods resting in S′.

History

Albert Einstein announced his theory of special relativity in 1905,^[7] with Hermann Minkowski providing his graphical representation in 1908.^[8]

In Minkowski's 1908 paper there were three diagrams, first to illustrate the Lorentz transformation, then the partition of the plane by the light-cone, and finally illustration of worldlines.^[8] The first diagram used a branch of the unit hyperbola ${\displaystyle t^{2}-x^{2}=1}$ to show the locus of a unit of proper time depending on velocity, thus illustrating time dilation. The second diagram showed the conjugate hyperbola to calibrate space, where a similar stretching leaves the impression of FitzGerald contraction. In 1914 Ludwik Silberstein^[9] included a diagram of "Minkowski's representation of the Lorentz transformation". This diagram included the unit hyperbola, its conjugate, and a pair of conjugate diameters. Since the 1960s a version of this more complete configuration has been referred to as The Minkowski Diagram, and used as a standard illustration of the transformation geometry of special relativity. E. T. Whittaker has pointed out that the principle of relativity is tantamount to the arbitrariness of what hyperbola radius is selected for time in the Minkowski diagram. In 1912 Gilbert N. Lewis and Edwin B. Wilson applied the methods of synthetic geometry to develop the properties of the non-Euclidean plane that has Minkowski diagrams.^[10][11]

When Taylor and Wheeler composed Spacetime Physics (1966), they did not use the term Minkowski diagram for their spacetime geometry. Instead they included an acknowledgement of Minkowski's contribution to philosophy by the totality of his innovation of 1908.^[12]

Loedel diagrams

While a frame at rest in a Minkowski diagram has orthogonal spacetime axes, a frame moving relative to the rest frame in a Minkowski diagram has spacetime axes which form an acute angle. This asymmetry of Minkowski diagrams can be misleading, since special relativity postulates that any two inertial reference frames must be physically equivalent. The Loedel diagram is an alternative spacetime diagram that makes the symmetry of inertial references frames much more manifest.

Formulation via median frame

Fig. 3-1: View in the median frame

Fig. 3-2: Symmetric diagram

Several authors showed that there is a frame of reference between the resting and moving ones where their symmetry would be apparent ("median frame").^[13] In this frame, the two other frames are moving in opposite directions with equal speed. Using such coordinates makes the units of length and time the same for both axes. If β = v/c and ${\textstyle \gamma =\left(1-\beta ^{2}\right)^{-{\frac {1}{2}}}}$ are given between ${\displaystyle S}$ and ${\displaystyle S^{\prime }}$, then these expressions are connected with the values in their median frame S₀ as follows:^[13][14]

${\displaystyle {\begin{aligned}&(1)&\beta &={\frac {2\beta _{0}}{1+{\beta _{0}}^{2}}},\\&(2)&\beta _{0}&={\frac {\gamma -1}{\beta \gamma }}.\end{aligned}}}$

For instance, if β = 0.5 between ${\displaystyle S}$ and ${\displaystyle S^{\prime }}$, then by (2) they are moving in their median frame S₀ with approximately ±0.268c each in opposite directions. On the other hand, if β₀ = 0.5 in S₀, then by (1) the relative velocity between ${\displaystyle S}$ and ${\displaystyle S^{\prime }}$ in their own rest frames is 0.8c. The construction of the axes of ${\displaystyle S}$ and ${\displaystyle S^{\prime }}$ is done in accordance with the ordinary method using tan α = β₀ with respect to the orthogonal axes of the median frame (Fig. 3-1).

However, it turns out that when drawing such a symmetric diagram, it is possible to derive the diagram's relations even without mentioning the median frame and β₀ at all. Instead, the relative velocity β = v/c between ${\displaystyle S}$ and ${\displaystyle S^{\prime }}$ can directly be used in the following construction, providing the same result:^[15]

If φ is the angle between the axes of ct′ and ct (or between x and x′), and θ between the axes of x′ and ct′, it is given:^{[15][16][17][18]}

${\displaystyle {\begin{aligned}\sin \varphi =\cos \theta &=\beta ,\\\cos \varphi =\sin \theta &={\frac {1}{\gamma }},\\\tan \varphi =\cot \theta &=\beta \gamma .\end{aligned}}}$

Two methods of construction are obvious from Fig. 3-2: the x-axis is drawn perpendicular to the ct′-axis, the x′ and ct-axes are added at angle φ; and the x′-axis is drawn at angle θ with respect to the ct′-axis, the x-axis is added perpendicular to the ct′-axis and the ct-axis perpendicular to the x′-axis.

In a Minkowski diagram, lengths on the page cannot be directly compared to each other, due to warping factor between the axes' unit lengths in a Minkowski diagram. In particular, if ${\displaystyle U}$ and ${\displaystyle U^{\prime }}$ are the unit lengths of the rest frame axes and moving frame axes, respectively, in a Minkowski diagram, then the two unit lengths are warped relative to each other via the formula:

${\displaystyle U^{\mathrm{\prime <!--\; \prime \; -->}}=U\sqrt{\frac{}{}}}$Zdroj:https://en.wikipedia.org?pojem=Spacetime_diagram
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---