
A | B | C | D | E | F | G | H | CH | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
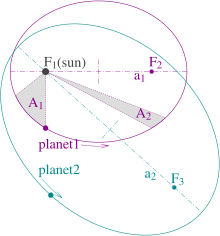
- The orbits are ellipses, with foci F1 and F2 for Planet 1, and F1 and F3 for Planet 2. The Sun is at F1.
- The shaded areas A1 and A2 are equal, and are swept out in equal times by Planet 1's orbit.
- The ratio of Planet 1's orbit time to Planet 2's is .
| Part of a series on |
| Astrodynamics |
|---|
In astronomy, Kepler's laws of planetary motion, published by Johannes Kepler between 1609 and 1619, describe the orbits of planets around the Sun. The laws modified the heliocentric theory of Nicolaus Copernicus, replacing its circular orbits and epicycles with elliptical trajectories, and explaining how planetary velocities vary. The three laws state that:[1][2]
- The orbit of a planet is an ellipse with the Sun at one of the two foci.
- A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time.
- The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit.
The elliptical orbits of planets were indicated by calculations of the orbit of Mars. From this, Kepler inferred that other bodies in the Solar System, including those farther away from the Sun, also have elliptical orbits. The second law helps to establish that when a planet is closer to the Sun, it travels faster. The third law expresses that the farther a planet is from the Sun, the slower its orbital speed, and vice versa.
Isaac Newton showed in 1687 that relationships like Kepler's would apply in the Solar System as a consequence of his own laws of motion and law of universal gravitation.
A more precise historical approach is found in Astronomia nova and Epitome Astronomiae Copernicanae.
Comparison to Copernicus
Johannes Kepler's laws improved the model of Copernicus. According to Copernicus:[3][4]
- The planetary orbit is a circle with epicycles.
- The Sun is approximately at the center of the orbit.
- The speed of the planet in the main orbit is constant.
Despite being correct in saying that the planets revolved around the Sun, Copernicus was incorrect in defining their orbits. Introducing physical explanations for movement in space beyond just geometry, Kepler correctly defined the orbit of planets as follows:[1][2][5]: 53–54
- The planetary orbit is not a circle with epicycles, but an ellipse.
- The Sun is not at the center but at a focal point of the elliptical orbit.
- Neither the linear speed nor the angular speed of the planet in the orbit is constant, but the area speed (closely linked historically with the concept of angular momentum) is constant.
The eccentricity of the orbit of the Earth makes the time from the March equinox to the September equinox, around 186 days, unequal to the time from the September equinox to the March equinox, around 179 days. A diameter would cut the orbit into equal parts, but the plane through the Sun parallel to the equator of the Earth cuts the orbit into two parts with areas in a 186 to 179 ratio, so the eccentricity of the orbit of the Earth is approximately
which is close to the correct value (0.016710218). The accuracy of this calculation requires that the two dates chosen be along the elliptical orbit's minor axis and that the midpoints of each half be along the major axis. As the two dates chosen here are equinoxes, this will be correct when perihelion, the date the Earth is closest to the Sun, falls on a solstice. The current perihelion, near January 4, is fairly close to the solstice of December 21 or 22.
Nomenclature
It took nearly two centuries for the current formulation of Kepler's work to take on its settled form. Voltaire's Eléments de la philosophie de Newton (Elements of Newton's Philosophy) of 1738 was the first publication to use the terminology of "laws".[6][7] The Biographical Encyclopedia of Astronomers in its article on Kepler (p. 620) states that the terminology of scientific laws for these discoveries was current at least from the time of Joseph de Lalande.[8] It was the exposition of Robert Small, in An account of the astronomical discoveries of Kepler (1814) that made up the set of three laws, by adding in the third.[9] Small also claimed, against the history, that these were empirical laws, based on inductive reasoning.[7][10]
Further, the current usage of "Kepler's Second Law" is something of a misnomer. Kepler had two versions, related in a qualitative sense: the "distance law" and the "area law". The "area law" is what became the Second Law in the set of three; but Kepler did himself not privilege it in that way.[11]
History
Kepler published his first two laws about planetary motion in 1609,[12] having found them by analyzing the astronomical observations of Tycho Brahe.[13][14][15][5]: 53 Kepler's third law was published in 1619.[16][14] Kepler had believed in the Copernican model of the Solar System, which called for circular orbits, but he could not reconcile Brahe's highly precise observations with a circular fit to Mars' orbit – Mars coincidentally having the highest eccentricity of all planets except Mercury.[17] His first law reflected this discovery.
In 1621, Kepler noted that his third law applies to the four brightest moons of Jupiter.[Nb 1] Godefroy Wendelin also made this observation in 1643.[Nb 2] The second law, in the "area law" form, was contested by Nicolaus Mercator in a book from 1664, but by 1670 his Philosophical Transactions were in its favour.[18][19] As the century proceeded it became more widely accepted.[20] The reception in Germany changed noticeably between 1688, the year in which Newton's Principia was published and was taken to be basically Copernican, and 1690, by which time work of Gottfried Leibniz on Kepler had been published.[21]
Newton was credited with understanding that the second law is not special to the inverse square law of gravitation, being a consequence just of the radial nature of that law, whereas the other laws do depend on the inverse square form of the attraction. Carl Runge and Wilhelm Lenz much later identified a symmetry principle in the phase space of planetary motion (the orthogonal group O(4) acting) which accounts for the first and third laws in the case of Newtonian gravitation, as conservation of angular momentum does via rotational symmetry for the second law.[22]
Formulary
The mathematical model of the kinematics of a planet subject to the laws allows a large range of further calculations.
First law
The orbit of every planet is an ellipse with the sun at one of the two foci.

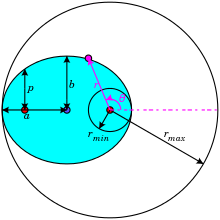
Mathematically, an ellipse can be represented by the formula:
where is the semi-latus rectum, ε is the eccentricity of the ellipse, r is the distance from the Sun to the planet, and θ is the angle to the planet's current position from its closest approach, as seen from the Sun. So (r, θ) are polar coordinates.
For an ellipse 0 < ε < 1 ; in the limiting case ε = 0, the orbit is a circle with the Sun at the centre (i.e. where there is zero eccentricity).
At θ = 0°, perihelion, the distance is minimum
At θ = 90° and at θ = 270° the distance is equal to .
At θ = 180°, aphelion, the distance is maximum (by definition, aphelion is – invariably – perihelion plus 180°)
The semi-major axis a is the arithmetic mean between rmin and rmax:
The semi-minor axis b is the geometric mean between rmin and rmax:
The semi-latus rectum p is the harmonic mean between rmin and rmax:
The eccentricity ε is the coefficient of variation between rmin and rmax:
The area of the ellipse is
The special case of a circle is ε = 0, resulting in r = p = rmin = rmax = a = b and A = πr2.
Second law
A line joining a planet and the Sun sweeps out equal areas during equal intervals of time.[23]
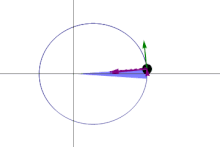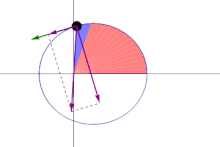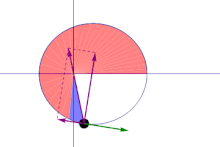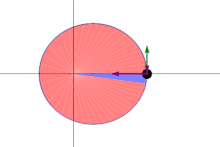
The orbital radius and angular velocity of the planet in the elliptical orbit will vary. This is shown in the animation: the planet travels faster when closer to the Sun, then slower when farther from the Sun. Kepler's second law states that the blue sector has constant area.
In a small time the planet sweeps out a small triangle having base line and height and area , so the constant areal velocity is
Antropológia
Aplikované vedy
Bibliometria
Dejiny vedy
Encyklopédie
Filozofia vedy
Forenzné vedy
Humanitné vedy
Knižničná veda
Kryogenika
Kryptológia
Kulturológia
Literárna veda
Medzidisciplinárne oblasti
Metódy kvantitatívnej analýzy
Metavedy
Metodika
Text je dostupný za podmienok Creative
Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších
podmienok.
Podrobnejšie informácie nájdete na stránke Podmienky
použitia.
www.astronomia.sk | www.biologia.sk | www.botanika.sk | www.dejiny.sk | www.economy.sk | www.elektrotechnika.sk | www.estetika.sk | www.farmakologia.sk | www.filozofia.sk | Fyzika | www.futurologia.sk | www.genetika.sk | www.chemia.sk | www.lingvistika.sk | www.politologia.sk | www.psychologia.sk | www.sexuologia.sk | www.sociologia.sk | www.veda.sk I www.zoologia.sk















