In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point (analogous to the origin of a Cartesian coordinate system) is called the pole, and the ray from the pole in the reference direction is the polar axis. The distance from the pole is called the radial coordinate, radial distance or simply radius, and the angle is called the angular coordinate, polar angle, or azimuth.^[1] Angles in polar notation are generally expressed in either degrees or radians (2π rad being equal to 360°).

Grégoire de Saint-Vincent and Bonaventura Cavalieri independently introduced the concepts in the mid-17th century, though the actual term "polar coordinates" has been attributed to Gregorio Fontana in the 18th century. The initial motivation for the introduction of the polar system was the study of circular and orbital motion.

Polar coordinates are most appropriate in any context where the phenomenon being considered is inherently tied to direction and length from a center point in a plane, such as spirals. Planar physical systems with bodies moving around a central point, or phenomena originating from a central point, are often simpler and more intuitive to model using polar coordinates.

The polar coordinate system is extended to three dimensions in two ways: the cylindrical and spherical coordinate systems.

History

The concepts of angle and radius were already used by ancient peoples of the first millennium BC. The Greek astronomer and astrologer Hipparchus (190–120 BC) created a table of chord functions giving the length of the chord for each angle, and there are references to his using polar coordinates in establishing stellar positions.^[2] In On Spirals, Archimedes describes the Archimedean spiral, a function whose radius depends on the angle. The Greek work, however, did not extend to a full coordinate system.

From the 8th century AD onward, astronomers developed methods for approximating and calculating the direction to Mecca (qibla)—and its distance—from any location on the Earth.^[3] From the 9th century onward they were using spherical trigonometry and map projection methods to determine these quantities accurately. The calculation is essentially the conversion of the equatorial polar coordinates of Mecca (i.e. its longitude and latitude) to its polar coordinates (i.e. its qibla and distance) relative to a system whose reference meridian is the great circle through the given location and the Earth's poles and whose polar axis is the line through the location and its antipodal point.^[4]

There are various accounts of the introduction of polar coordinates as part of a formal coordinate system. The full history of the subject is described in Harvard professor Julian Lowell Coolidge's Origin of Polar Coordinates.^[5] Grégoire de Saint-Vincent and Bonaventura Cavalieri independently introduced the concepts in the mid-seventeenth century. Saint-Vincent wrote about them privately in 1625 and published his work in 1647, while Cavalieri published his in 1635 with a corrected version appearing in 1653. Cavalieri first used polar coordinates to solve a problem relating to the area within an Archimedean spiral. Blaise Pascal subsequently used polar coordinates to calculate the length of parabolic arcs.

In Method of Fluxions (written 1671, published 1736), Sir Isaac Newton examined the transformations between polar coordinates, which he referred to as the "Seventh Manner; For Spirals", and nine other coordinate systems.^[6] In the journal Acta Eruditorum (1691), Jacob Bernoulli used a system with a point on a line, called the pole and polar axis respectively. Coordinates were specified by the distance from the pole and the angle from the polar axis. Bernoulli's work extended to finding the radius of curvature of curves expressed in these coordinates.

The actual term polar coordinates has been attributed to Gregorio Fontana and was used by 18th-century Italian writers. The term appeared in English in George Peacock's 1816 translation of Lacroix's Differential and Integral Calculus.^[7][8] Alexis Clairaut was the first to think of polar coordinates in three dimensions, and Leonhard Euler was the first to actually develop them.^[5]

Conventions

The radial coordinate is often denoted by r or ρ, and the angular coordinate by φ, θ, or t. The angular coordinate is specified as φ by ISO standard 31-11. However, in mathematical literature the angle is often denoted by θ instead.

Angles in polar notation are generally expressed in either degrees or radians (2π rad being equal to 360°). Degrees are traditionally used in navigation, surveying, and many applied disciplines, while radians are more common in mathematics and mathematical physics.^[9]

The angle φ is defined to start at 0° from a reference direction, and to increase for rotations in either clockwise (cw) or counterclockwise (ccw) orientation. For example, in mathematics, the reference direction is usually drawn as a ray from the pole horizontally to the right, and the polar angle increases to positive angles for ccw rotations, whereas in navigation (bearing, heading) the 0°-heading is drawn vertically upwards and the angle increases for cw rotations. The polar angles decrease towards negative values for rotations in the respectively opposite orientations.

Uniqueness of polar coordinates

Adding any number of full turns (360°) to the angular coordinate does not change the corresponding direction. Similarly, any polar coordinate is identical to the coordinate with the negative radial component and the opposite direction (adding 180° to the polar angle). Therefore, the same point (r, φ) can be expressed with an infinite number of different polar coordinates (r, φ + n × 360°) and (−r, φ + 180° + n × 360°) = (−r, φ + (2n + 1) × 180°), where n is an arbitrary integer.^[10] Moreover, the pole itself can be expressed as (0, φ) for any angle φ.^[11]

Where a unique representation is needed for any point besides the pole, it is usual to limit r to positive numbers (r > 0) and φ to either the interval [0, 360°) or the interval (−180°, 180°], which in radians are [0, 2π) or (−π, π].^[12] Another convention, in reference to the usual codomain of the arctan function, is to allow for arbitrary nonzero real values of the radial component and restrict the polar angle to (−90°, 90°]. In all cases a unique azimuth for the pole (r = 0) must be chosen, e.g., φ = 0.

Converting between polar and Cartesian coordinates

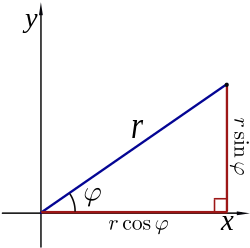
The polar coordinates r and φ can be converted to the Cartesian coordinates x and y by using the trigonometric functions sine and cosine:

The Cartesian coordinates x and y can be converted to polar coordinates r and φ with r ≥ 0 and φ in the interval (−π, π by:^[13]

where hypot is the Pythagorean sum and atan2 is a common variation on the arctangent function defined as

If r is calculated first as above, then this formula for φ may be stated more simply using the arccosine function:

Complex numbers

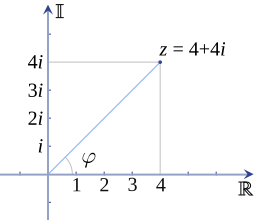
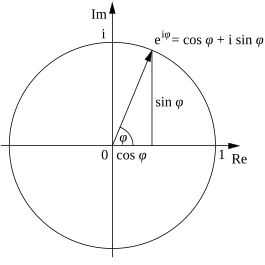
Every complex number can be represented as a point in the complex plane, and can therefore be expressed by specifying either the point's Cartesian coordinates (called rectangular or Cartesian form) or the point's polar coordinates (called polar form).

In polar form, the distance and angle coordinates are often referred to as the number's magnitude and argument respectively. Two complex numbers can be multiplied by adding their arguments and multiplying their magnitudes.

The complex number z can be represented in rectangular form as

where i is the imaginary unit, or can alternatively be written in polar form as and from there, by Euler's formula,^[14] as where e is Euler's number, and φ, expressed in radians, is the principal value of the complex number function arg applied to x + iy. To convert between the rectangular and polar forms of a complex number, the conversion formulae given above can be used. Equivalent are the cis and angle notations:

For the operations of multiplication, division, exponentiation, and root extraction of complex numbers, it is generally much simpler to work with complex numbers expressed in polar form rather than rectangular form. From the laws of exponentiation:

Multiplication

${\displaystyle r_0{e}^{i{\mathrm{\phi <!--\; \phi \; -->}}_0}{}_{}}$Zdroj:https://en.wikipedia.org?pojem=Polar_coordinates
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---