Geometry
Projecting a sphere to a plane
Outline History (Timeline)
Branches Euclidean Non-Euclidean Elliptic Spherical Hyperbolic Non-Archimedean geometry Projective Affine Synthetic Analytic Algebraic Arithmetic Diophantine Differential Riemannian Symplectic Discrete differential Complex Finite Discrete/Combinatorial Digital Convex Computational Fractal Incidence Noncommutative geometry Noncommutative algebraic geometry
Concepts Features Dimension Straightedge and compass constructions Angle Curve Diagonal Orthogonality (Perpendicular) Parallel Vertex Congruence Similarity Symmetry
Zero-dimensional Point
One-dimensional Line segment ray Length
Two-dimensional Plane Area Polygon Triangle Altitude Hypotenuse Pythagorean theorem Parallelogram Square Rectangle Rhombus Rhomboid Quadrilateral Trapezoid Kite Circle Diameter Circumference Area
Three-dimensional Volume Cube cuboid Cylinder Dodecahedron Icosahedron Octahedron Pyramid Platonic Solid Sphere Tetrahedron
Four- / other-dimensional Tesseract Hypersphere
Geometers
by name Aida Aryabhata Ahmes Alhazen Apollonius Archimedes Atiyah Baudhayana Bolyai Brahmagupta Cartan Coxeter Descartes Euclid Euler Gauss Gromov Hilbert Huygens Jyeṣṭhadeva Kātyāyana Khayyám Klein Lobachevsky Manava Minkowski Minggatu Pascal Pythagoras Parameshvara Poincaré Riemann Sakabe Sijzi al-Tusi Veblen Virasena Yang Hui al-Yasamin Zhang List of geometers
by period BCE Ahmes Baudhayana Manava Pythagoras Euclid Archimedes Apollonius 1–1400s Zhang Kātyāyana Aryabhata Brahmagupta Virasena Alhazen Sijzi Khayyám al-Yasamin al-Tusi Yang Hui Parameshvara 1400s–1700s Jyeṣṭhadeva Descartes Pascal Huygens Minggatu Euler Sakabe Aida 1700s–1900s Gauss Lobachevsky Bolyai Riemann Klein Poincaré Hilbert Minkowski Cartan Veblen Coxeter Present day Atiyah Gromov
v t e

In geometry, a straight line, usually abbreviated line, is an infinitely long object with no width, depth, or curvature, an idealization of such physical objects as a straightedge, a taut string, or a ray of light. Lines are spaces of dimension one, which may be embedded in spaces of dimension two, three, or higher. The word line may also refer, in everyday life, to a line segment, which is a part of a line delimited by two points (its endpoints).

Euclid's Elements defines a straight line as a "breadthless length" that "lies evenly with respect to the points on itself", and introduced several postulates as basic unprovable properties on which the rest of geometry was established. Euclidean line and Euclidean geometry are terms introduced to avoid confusion with generalizations introduced since the end of the 19th century, such as non-Euclidean, projective, and affine geometry.

Properties

In the Greek deductive geometry of Euclid's Elements, a general line (now called a curve) is defined as a "breadthless length", and a straight line (now called a line segment) was defined as a line "which lies evenly with the points on itself".^[1]: 291 These definitions appeal to readers' physical experience, relying on terms that are not themselves defined, and the definitions are never explicitly referenced in the remainder of the text. In modern geometry, a line is usually either taken as a primitive notion with properties given by axioms,^[1]: 95 or else defined as a set of points obeying a linear relationship, for instance when real numbers are taken to be primitive and geometry is established analytically in terms of numerical coordinates.

In an axiomatic formulation of Euclidean geometry, such as that of Hilbert (modern mathematicians added to Euclid's original axioms to fill perceived logical gaps),^[1]: 108 a line is stated to have certain properties that relate it to other lines and points. For example, for any two distinct points, there is a unique line containing them, and any two distinct lines intersect at most at one point.^[1]: 300 In two dimensions (i.e., the Euclidean plane), two lines that do not intersect are called parallel. In higher dimensions, two lines that do not intersect are parallel if they are contained in a plane, or skew if they are not.

On a Euclidean plane, a line can be represented as a boundary between two regions.^[2]: 104 Any collection of finitely many lines partitions the plane into convex polygons (possibly unbounded); this partition is known as an arrangement of lines.

In higher dimensions

In three-dimensional space, a first degree equation in the variables x, y, and z defines a plane, so two such equations, provided the planes they give rise to are not parallel, define a line which is the intersection of the planes. More generally, in n-dimensional space n−1 first-degree equations in the n coordinate variables define a line under suitable conditions.

In more general Euclidean space, Rⁿ (and analogously in every other affine space), the line L passing through two different points a and b is the subset

The direction of the line is from a reference point a (t = 0) to another point b (t = 1), or in other words, in the direction of the vector b − a. Different choices of a and b can yield the same line.

Collinear points

Three points are said to be collinear if they lie on the same line. Three points usually determine a plane, but in the case of three collinear points this does not happen.

In affine coordinates, in n-dimensional space the points X = (x₁, x₂, ..., x_n), Y = (y₁, y₂, ..., y_n), and Z = (z₁, z₂, ..., z_n) are collinear if the matrix

has a rank less than 3. In particular, for three points in the plane (n = 2), the above matrix is square and the points are collinear if and only if its determinant is zero.

Equivalently for three points in a plane, the points are collinear if and only if the slope between one pair of points equals the slope between any other pair of points (in which case the slope between the remaining pair of points will equal the other slopes). By extension, k points in a plane are collinear if and only if any (k–1) pairs of points have the same pairwise slopes.

In Euclidean geometry, the Euclidean distance d(a,b) between two points a and b may be used to express the collinearity between three points by:^[3][4]

The points a, b and c are collinear if and only if d(x,a) = d(c,a) and d(x,b) = d(c,b) implies x = c.

However, there are other notions of distance (such as the Manhattan distance) for which this property is not true.

In the geometries where the concept of a line is a primitive notion, as may be the case in some synthetic geometries, other methods of determining collinearity are needed.

Types

In a sense,^[a] all lines in Euclidean geometry are equal, in that, without coordinates, one can not tell them apart from one another. However, lines may play special roles with respect to other objects in the geometry and be divided into types according to that relationship. For instance, with respect to a conic (a circle, ellipse, parabola, or hyperbola), lines can be:

• tangent lines, which touch the conic at a single point;
• secant lines, which intersect the conic at two points and pass through its interior;^[5]
• exterior lines, which do not meet the conic at any point of the Euclidean plane; or
• a directrix, whose distance from a point helps to establish whether the point is on the conic.
• a coordinate line, a linear coordinate dimension

In the context of determining parallelism in Euclidean geometry, a transversal is a line that intersects two other lines that may or not be parallel to each other.

For more general algebraic curves, lines could also be:

• i-secant lines, meeting the curve in i points counted without multiplicity, or
• asymptotes, which a curve approaches arbitrarily closely without touching it.^[6]

With respect to triangles we have:

• the Euler line,
• the Simson lines, and
• central lines.

For a convex quadrilateral with at most two parallel sides, the Newton line is the line that connects the midpoints of the two diagonals.^[7]

For a hexagon with vertices lying on a conic we have the Pascal line and, in the special case where the conic is a pair of lines, we have the Pappus line.

Parallel lines are lines in the same plane that never cross. Intersecting lines share a single point in common. Coincidental lines coincide with each other—every point that is on either one of them is also on the other.

Perpendicular lines are lines that intersect at right angles.^[8]

In three-dimensional space, skew lines are lines that are not in the same plane and thus do not intersect each other.

In axiomatic systems

The concept of line is often considered in geometry as a primitive notion in axiomatic systems,^[1]: 95 meaning it is not being defined by other concepts.^[9] In those situations where a line is a defined concept, as in coordinate geometry, some other fundamental ideas are taken as primitives. When the line concept is a primitive, the properties of lines are dictated by the axioms which they must satisfy.

In a non-axiomatic or simplified axiomatic treatment of geometry, the concept of a primitive notion may be too abstract to be dealt with. In this circumstance, it is possible to provide a description or mental image of a primitive notion, to give a foundation to build the notion on which would formally be based on the (unstated) axioms. Descriptions of this type may be referred to, by some authors, as definitions in this informal style of presentation. These are not true definitions, and could not be used in formal proofs of statements. The "definition" of line in Euclid's Elements falls into this category.^[1]: 95 Even in the case where a specific geometry is being considered (for example, Euclidean geometry), there is no generally accepted agreement among authors as to what an informal description of a line should be when the subject is not being treated formally.

Definition

Linear equation

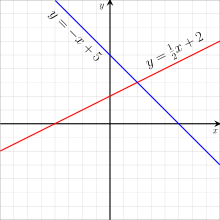
Lines in a Cartesian plane or, more generally, in affine coordinates, are characterized by linear equations. More precisely, every line ${\displaystyle L}$ (including vertical lines) is the set of all points whose coordinates (x, y) satisfy a linear equation; that is,

where a, b and c are fixed real numbers (called coefficients) such that a and b are not both zero. Using this form, vertical lines correspond to equations with b = 0.

One can further suppose either c = 1 or c = 0, by dividing everything by c if it is not zero.

There are many variant ways to write the equation of a line which can all be converted from one to another by algebraic manipulation. The above form is sometimes called the standard form. If the constant term is put on the left, the equation becomes

and this is sometimes called the general form of the equation. However, this terminology is not universally accepted, and many authors do not distinguish these two forms.

These forms are generally named by the type of information (data) about the line that is needed to write down the form. Some of the important data of a line is its slope, x-intercept, known points on the line and y-intercept.

The equation of the line passing through two different points ${\displaystyle P_{0}(x_{0},y_{0})}$ and ${\displaystyle P_{1}(x_{1},y_{1})}$ may be written as

If x₀ ≠ x₁, this equation may be rewritten as