Differential geometry of curves is the branch of geometry that deals with smooth curves in the plane and the Euclidean space by methods of differential and integral calculus.

Many specific curves have been thoroughly investigated using the synthetic approach. Differential geometry takes another path: curves are represented in a parametrized form, and their geometric properties and various quantities associated with them, such as the curvature and the arc length, are expressed via derivatives and integrals using vector calculus. One of the most important tools used to analyze a curve is the Frenet frame, a moving frame that provides a coordinate system at each point of the curve that is "best adapted" to the curve near that point.

The theory of curves is much simpler and narrower in scope than the theory of surfaces and its higher-dimensional generalizations because a regular curve in a Euclidean space has no intrinsic geometry. Any regular curve may be parametrized by the arc length (the natural parametrization). From the point of view of a theoretical point particle on the curve that does not know anything about the ambient space, all curves would appear the same. Different space curves are only distinguished by how they bend and twist. Quantitatively, this is measured by the differential-geometric invariants called the curvature and the torsion of a curve. The fundamental theorem of curves asserts that the knowledge of these invariants completely determines the curve.

Definitions

A parametric C^r-curve or a C^r-parametrization is a vector-valued function

that is r-times continuously differentiable (that is, the component functions of γ are continuously differentiable), where ${\displaystyle n\in \mathbb {N} }$, ${\displaystyle r\in \mathbb {N} \cup \{\infty \}}$, and I is a non-empty interval of real numbers. The image of the parametric curve is ${\displaystyle \gamma \subseteq \mathbb {R} ^{n}}$. The parametric curve γ and its image γ must be distinguished because a given subset of ${\displaystyle \mathbb {R} ^{n}}$ can be the image of many distinct parametric curves. The parameter t in γ(t) can be thought of as representing time, and γ the trajectory of a moving point in space. When I is a closed interval , γ(a) is called the starting point and γ(b) is the endpoint of γ. If the starting and the end points coincide (that is, γ(a) = γ(b)), then γ is a closed curve or a loop. To be a C^r-loop, the function γ must be r-times continuously differentiable and satisfy γ^(k)(a) = γ^(k)(b) for 0 ≤ k ≤ r.

The parametric curve is simple if

is injective. It is analytic if each component function of γ is an analytic function, that is, it is of class C^ω.

The curve γ is regular of order m (where m ≤ r) if, for every t ∈ I,

is a linearly independent subset of ${\displaystyle \mathbb {R} ^{n}}$. In particular, a parametric C¹-curve γ is regular if and only if γ′(t) ≠ 0 for any t ∈ I.

Re-parametrization and equivalence relation

Given the image of a parametric curve, there are several different parametrizations of the parametric curve. Differential geometry aims to describe the properties of parametric curves that are invariant under certain reparametrizations. A suitable equivalence relation on the set of all parametric curves must be defined. The differential-geometric properties of a parametric curve (such as its length, its Frenet frame, and its generalized curvature) are invariant under reparametrization and therefore properties of the equivalence class itself. The equivalence classes are called C^r-curves and are central objects studied in the differential geometry of curves.

Two parametric C^r-curves, ${\displaystyle \gamma _{1}:I_{1}\to \mathbb {R} ^{n}}$ and ${\displaystyle \gamma _{2}:I_{2}\to \mathbb {R} ^{n}}$, are said to be equivalent if and only if there exists a bijective C^r-map φ : I₁ → I₂ such that

and γ₂ is then said to be a re-parametrization of γ₁.

Re-parametrization defines an equivalence relation on the set of all parametric C^r-curves of class C^r. The equivalence class of this relation simply a C^r-curve.

An even finer equivalence relation of oriented parametric C^r-curves can be defined by requiring φ to satisfy φ′(t) > 0.

Equivalent parametric C^r-curves have the same image, and equivalent oriented parametric C^r-curves even traverse the image in the same direction.

Length and natural parametrization

The length l of a parametric C¹-curve ${\displaystyle \gamma :\to \mathbb {R} ^{n}}$ is defined as

The length of a parametric curve is invariant under reparametrization and is therefore a differential-geometric property of the parametric curve.

For each regular parametric C^r-curve ${\displaystyle \gamma :\to \mathbb {R} ^{n}}$, where r ≥ 1, the function is defined

Writing γ(s) = γ(t(s)), where t(s) is the inverse function of s(t). This is a re-parametrization γ of γ that is called an arc-length parametrization, natural parametrization, unit-speed parametrization. The parameter s(t) is called the natural parameter of γ.

This parametrization is preferred because the natural parameter s(t) traverses the image of γ at unit speed, so that

In practice, it is often very difficult to calculate the natural parametrization of a parametric curve, but it is useful for theoretical arguments.

For a given parametric curve γ, the natural parametrization is unique up to a shift of parameter.

The quantity

is sometimes called the energy or action of the curve; this name is justified because the geodesic equations are the Euler–Lagrange equations of motion for this action.

Frenet frame

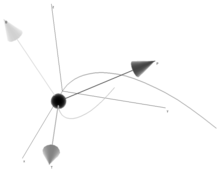
A Frenet frame is a moving reference frame of n orthonormal vectors e_i(t) which are used to describe a curve locally at each point γ(t). It is the main tool in the differential geometric treatment of curves because it is far easier and more natural to describe local properties (e.g. curvature, torsion) in terms of a local reference system than using a global one such as Euclidean coordinates.

Given a C^{n + 1}-curve γ in $$Zdroj:https://en.wikipedia.org?pojem=Differential_geometry_of_curves
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---