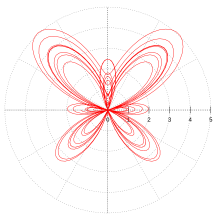
In mathematics, a parametric equation defines a group of quantities as functions of one or more independent variables called parameters.^[1] Parametric equations are commonly used to express the coordinates of the points that make up a geometric object such as a curve or surface, called a parametric curve and parametric surface, respectively. In such cases, the equations are collectively called a parametric representation,^[2] or parametric system,^[3] or parameterization (alternatively spelled as parametrisation) of the object.^[1][4][5]

For example, the equations

form a parametric representation of the unit circle, where t is the parameter: A point (x, y) is on the unit circle if and only if there is a value of t such that these two equations generate that point. Sometimes the parametric equations for the individual scalar output variables are combined into a single parametric equation in vectors:

Parametric representations are generally nonunique (see the "Examples in two dimensions" section below), so the same quantities may be expressed by a number of different parameterizations.^[1]

In addition to curves and surfaces, parametric equations can describe manifolds and algebraic varieties of higher dimension, with the number of parameters being equal to the dimension of the manifold or variety, and the number of equations being equal to the dimension of the space in which the manifold or variety is considered (for curves the dimension is one and one parameter is used, for surfaces dimension two and two parameters, etc.).

Parametric equations are commonly used in kinematics, where the trajectory of an object is represented by equations depending on time as the parameter. Because of this application, a single parameter is often labeled t; however, parameters can represent other physical quantities (such as geometric variables) or can be selected arbitrarily for convenience. Parameterizations are non-unique; more than one set of parametric equations can specify the same curve.^[6]

Applications

Kinematics

In kinematics, objects' paths through space are commonly described as parametric curves, with each spatial coordinate depending explicitly on an independent parameter (usually time). Used in this way, the set of parametric equations for the object's coordinates collectively constitute a vector-valued function for position. Such parametric curves can then be integrated and differentiated termwise. Thus, if a particle's position is described parametrically as

then its velocity can be found as

and its acceleration as

Computer-aided design

Another important use of parametric equations is in the field of computer-aided design (CAD).^[7] For example, consider the following three representations, all of which are commonly used to describe planar curves.

Type	Form	Example	Description
Explicit	${\displaystyle y=f(x)\,\!}$	${\displaystyle y=mx+b\,\!}$	Line
Implicit	${\displaystyle f(x,y)=0\,\!}$	${\displaystyle \left(x-a\right)^{2}+\left(y-b\right)^{2}=r^{2}}$	Circle
Parametric	${\displaystyle x={\frac {g(t)}{w(t)}};\,\!}$ ${\displaystyle y={\frac {h(t)}{w(t)}}}$	${\displaystyle x=a_{0}+a_{1}t;\,\!}$ ${\displaystyle y=b_{0}+b_{1}t\,\!}$	Line
		${\displaystyle x=a+r\,\cos t;\,\!}$ ${\displaystyle y=b+r\,\sin t\,\!}$	Circle

Each representation has advantages and drawbacks for CAD applications.

The explicit representation may be very complicated, or even may not exist. Moreover, it does not behave well under geometric transformations, and in particular under rotations. On the other hand, as a parametric equation and an implicit equation may easily be deduced from an explicit representation, when a simple explicit representation exists, it has the advantages of both other representations.

Implicit representations may make it difficult to generate points on the curve, and even to decide whether there are real points. On the other hand, they are well suited for deciding whether a given point is on a curve, or whether it is inside or outside of a closed curve.

Such decisions may be difficult with a parametric representation, but parametric representations are best suited for generating points on a curve, and for plotting it.^[8]

Integer geometry

Numerous problems in integer geometry can be solved using parametric equations. A classical such solution is Euclid's parametrization of right triangles such that the lengths of their sides a, b and their hypotenuse c are coprime integers. As a and b are not both even (otherwise a, b and c would not be coprime), one may exchange them to have a even, and the parameterization is then

where the parameters m and n are positive coprime integers that are not both odd.

By multiplying a, b and c by an arbitrary positive integer, one gets a parametrization of all right triangles whose three sides have integer lengths.

Implicitization

Converting a set of parametric equations to a single implicit equation involves eliminating the variable t from the simultaneous equations $$Zdroj:https://en.wikipedia.org?pojem=Parametric_equation
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---