
A | B | C | D | E | F | G | H | CH | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9

| Part of a series on |
| Numeral systems |
|---|
| List of numeral systems |
Positional notation (or place-value notation, or positional numeral system) usually denotes the extension to any base of the Hindu–Arabic numeral system (or decimal system). More generally, a positional system is a numeral system in which the contribution of a digit to the value of a number is the value of the digit multiplied by a factor determined by the position of the digit. In early numeral systems, such as Roman numerals, a digit has only one value: I means one, X means ten and C a hundred (however, the values may be modified when combined). In modern positional systems, such as the decimal system, the position of the digit means that its value must be multiplied by some value: in 555, the three identical symbols represent five hundreds, five tens, and five units, respectively, due to their different positions in the digit string.
The Babylonian numeral system, base 60, was the first positional system to be developed, and its influence is present today in the way time and angles are counted in tallies related to 60, such as 60 minutes in an hour and 360 degrees in a circle. Today, the Hindu–Arabic numeral system (base ten) is the most commonly used system globally. However, the binary numeral system (base two) is used in almost all computers and electronic devices because it is easier to implement efficiently in electronic circuits.
Systems with negative base, complex base or negative digits have been described. Most of them do not require a minus sign for designating negative numbers.
The use of a radix point (decimal point in base ten), extends to include fractions and allows representing any real number with arbitrary accuracy. With positional notation, arithmetical computations are much simpler than with any older numeral system; this led to the rapid spread of the notation when it was introduced in western Europe.
History
Today, the base-10 (decimal) system, which is presumably motivated by counting with the ten fingers, is ubiquitous. Other bases have been used in the past, and some continue to be used today. For example, the Babylonian numeral system, credited as the first positional numeral system, was base-60. However, it lacked a real zero. Initially inferred only from context, later, by about 700 BC, zero came to be indicated by a "space" or a "punctuation symbol" (such as two slanted wedges) between numerals.[1] It was a placeholder rather than a true zero because it was not used alone or at the end of a number. Numbers like 2 and 120 (2×60) looked the same because the larger number lacked a final placeholder. Only context could differentiate them.
The polymath Archimedes (ca. 287–212 BC) invented a decimal positional system in his Sand Reckoner which was based on 108[2] and later led the German mathematician Carl Friedrich Gauss to lament what heights science would have already reached in his days if Archimedes had fully realized the potential of his ingenious discovery.[3] Hellenistic and Roman astronomers used a base-60 system based on the Babylonian model (see Greek numerals § Zero).
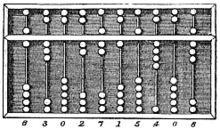
Before positional notation became standard, simple additive systems (sign-value notation) such as Roman numerals were used, and accountants in ancient Rome and during the Middle Ages used the abacus or stone counters to do arithmetic.[4]

Lower row horizontal form
Counting rods and most abacuses have been used to represent numbers in a positional numeral system. With counting rods or abacus to perform arithmetic operations, the writing of the starting, intermediate and final values of a calculation could easily be done with a simple additive system in each position or column. This approach required no memorization of tables (as does positional notation) and could produce practical results quickly.
The oldest extant positional notation system is either that of Chinese rod numerals, used from at least the early 8th century, or perhaps Khmer numerals, showing possible usages of positional-numbers in the 7th century. Khmer numerals and other Indian numerals originate with the Brahmi numerals of about the 3rd century BC, which symbols were, at the time, not used positionally. Medieval Indian numerals are positional, as are the derived Arabic numerals, recorded from the 10th century.
After the French Revolution (1789–1799), the new French government promoted the extension of the decimal system.[5] Some of those pro-decimal efforts—such as decimal time and the decimal calendar—were unsuccessful. Other French pro-decimal efforts—currency decimalisation and the metrication of weights and measures—spread widely out of France to almost the whole world.
History of positional fractions
J. Lennart Berggren notes that positional decimal fractions were used for the first time by Arab mathematician Abu'l-Hasan al-Uqlidisi as early as the 10th century.[6] The Jewish mathematician Immanuel Bonfils used decimal fractions around 1350, but did not develop any notation to represent them.[7] The Persian mathematician Jamshīd al-Kāshī made the same discovery of decimal fractions in the 15th century.[6] Al Khwarizmi introduced fractions to Islamic countries in the early 9th century; his fraction presentation was similar to the traditional Chinese mathematical fractions from Sunzi Suanjing.[8] This form of fraction with numerator on top and denominator at bottom without a horizontal bar was also used by 10th century Abu'l-Hasan al-Uqlidisi and 15th century Jamshīd al-Kāshī's work "Arithmetic Key".[8][9]
The adoption of the decimal representation of numbers less than one, a fraction, is often credited to Simon Stevin through his textbook De Thiende;[10] but both Stevin and E. J. Dijksterhuis indicate that Regiomontanus contributed to the European adoption of general decimals:[11]
- European mathematicians, when taking over from the Hindus, via the Arabs, the idea of positional value for integers, neglected to extend this idea to fractions. For some centuries they confined themselves to using common and sexagesimal fractions... This half-heartedness has never been completely overcome, and sexagesimal fractions still form the basis of our trigonometry, astronomy and measurement of time. ¶ ... Mathematicians sought to avoid fractions by taking the radius R equal to a number of units of length of the form 10n and then assuming for n so great an integral value that all occurring quantities could be expressed with sufficient accuracy by integers. ¶ The first to apply this method was the German astronomer Regiomontanus. To the extent that he expressed goniometrical line-segments in a unit R/10n, Regiomontanus may be called an anticipator of the doctrine of decimal positional fractions.[11]: 17, 18
In the estimation of Dijksterhuis, "after the publication of De Thiende only a small advance was required to establish the complete system of decimal positional fractions, and this step was taken promptly by a number of writers ... next to Stevin the most important figure in this development was Regiomontanus." Dijksterhuis noted that "gives full credit to Regiomontanus for his prior contribution, saying that the trigonometric tables of the German astronomer actually contain the whole theory of 'numbers of the tenth progress'."[11]: 19
Mathematics
Base of the numeral system
In mathematical numeral systems the radix r is usually the number of unique digits, including zero, that a positional numeral system uses to represent numbers. In some cases, such as with a negative base, the radix is the absolute value of the base b. For example, for the decimal system the radix (and base) is ten, because it uses the ten digits from 0 through 9. When a number "hits" 9, the next number will not be another different symbol, but a "1" followed by a "0". In binary, the radix is two, since after it hits "1", instead of "2" or another written symbol, it jumps straight to "10", followed by "11" and "100".
The highest symbol of a positional numeral system usually has the value one less than the value of the radix of that numeral system. The standard positional numeral systems differ from one another only in the base they use.
The radix is an integer that is greater than 1, since a radix of zero would not have any digits, and a radix of 1 would only have the zero digit. Negative bases are rarely used. In a system with more than unique digits, numbers may have many different possible representations.
It is important that the radix is finite, from which follows that the number of digits is quite low. Otherwise, the length of a numeral would not necessarily be logarithmic in its size.
(In certain non-standard positional numeral systems, including bijective numeration, the definition of the base or the allowed digits deviates from the above.)
In standard base-ten (decimal) positional notation, there are ten decimal digits and the number
- .
In standard base-sixteen (hexadecimal), there are the sixteen hexadecimal digits (0–9 and A–F) and the number
where B represents the number eleven as a single symbol.
In general, in base-b, there are b digits and the number
has Note that represents a sequence of digits, not multiplication.
Notation
When describing base in mathematical notation, the letter b is generally used as a symbol for this concept, so, for a binary system, b equals 2. Another common way of expressing the base is writing it as a decimal subscript after the number that is being represented (this notation is used in this article). 11110112 implies that the number 1111011 is a base-2 number, equal to 12310 (a decimal notation representation), 1738 (octal) and 7B16 (hexadecimal). In books and articles, when using initially the written abbreviations of number bases, the base is not subsequently printed: it is assumed that binary 1111011 is the same as 11110112.
The base b may also be indicated by the phrase "base-b". So binary numbers are "base-2"; octal numbers are "base-8"; decimal numbers are "base-10"; and so on.
To a given radix b the set of digits {0, 1, ..., b−2, b−1} is called the standard set of digits. Thus, binary numbers have digits {0, 1}; decimal numbers have digits {0, 1, 2, ..., 8, 9}; and so on. Therefore, the following are notational errors: 522, 22, 1A9. (In all cases, one or more digits is not in the set of allowed digits for the given base.)
Exponentiation
Positional numeral systems work using exponentiation of the base. A digit's value is the digit multiplied by the value of its place. Place values are the number of the base raised to the nth power, where n is the number of other digits between a given digit and the radix point. If a given digit is on the left hand side of the radix point (i.e. its value is an integer) then n is positive or zero; if the digit is on the right hand side of the radix point (i.e., its value is fractional) then n is negative.
As an example of usage, the number 465 in its respective base b (which must be at least base 7 because the highest digit in it is 6) is equal to:
Antropológia
Aplikované vedy
Bibliometria
Dejiny vedy
Encyklopédie
Filozofia vedy
Forenzné vedy
Humanitné vedy
Knižničná veda
Kryogenika
Kryptológia
Kulturológia
Literárna veda
Medzidisciplinárne oblasti
Metódy kvantitatívnej analýzy
Metavedy
Metodika
Text je dostupný za podmienok Creative
Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších
podmienok.
Podrobnejšie informácie nájdete na stránke Podmienky
použitia.
www.astronomia.sk | www.biologia.sk | www.botanika.sk | www.dejiny.sk | www.economy.sk | www.elektrotechnika.sk | www.estetika.sk | www.farmakologia.sk | www.filozofia.sk | Fyzika | www.futurologia.sk | www.genetika.sk | www.chemia.sk | www.lingvistika.sk | www.politologia.sk | www.psychologia.sk | www.sexuologia.sk | www.sociologia.sk | www.veda.sk I www.zoologia.sk









