In mathematics, a metric space is a set together with a notion of distance between its elements, usually called points. The distance is measured by a function called a metric or distance function.^[1] Metric spaces are the most general setting for studying many of the concepts of mathematical analysis and geometry.

The most familiar example of a metric space is 3-dimensional Euclidean space with its usual notion of distance. Other well-known examples are a sphere equipped with the angular distance and the hyperbolic plane. A metric may correspond to a metaphorical, rather than physical, notion of distance: for example, the set of 100-character Unicode strings can be equipped with the Hamming distance, which measures the number of characters that need to be changed to get from one string to another.

Since they are very general, metric spaces are a tool used in many different branches of mathematics. Many types of mathematical objects have a natural notion of distance and therefore admit the structure of a metric space, including Riemannian manifolds, normed vector spaces, and graphs. In abstract algebra, the p-adic numbers arise as elements of the completion of a metric structure on the rational numbers. Metric spaces are also studied in their own right in metric geometry^[2] and analysis on metric spaces.^[3]

Many of the basic notions of mathematical analysis, including balls, completeness, as well as uniform, Lipschitz, and Hölder continuity, can be defined in the setting of metric spaces. Other notions, such as continuity, compactness, and open and closed sets, can be defined for metric spaces, but also in the even more general setting of topological spaces.

Definition and illustration

Motivation

To see the utility of different notions of distance, consider the surface of the Earth as a set of points. We can measure the distance between two such points by the length of the shortest path along the surface, "as the crow flies"; this is particularly useful for shipping and aviation. We can also measure the straight-line distance between two points through the Earth's interior; this notion is, for example, natural in seismology, since it roughly corresponds to the length of time it takes for seismic waves to travel between those two points.

The notion of distance encoded by the metric space axioms has relatively few requirements. This generality gives metric spaces a lot of flexibility. At the same time, the notion is strong enough to encode many intuitive facts about what distance means. This means that general results about metric spaces can be applied in many different contexts.

Like many fundamental mathematical concepts, the metric on a metric space can be interpreted in many different ways. A particular metric may not be best thought of as measuring physical distance, but, instead, as the cost of changing from one state to another (as with Wasserstein metrics on spaces of measures) or the degree of difference between two objects (for example, the Hamming distance between two strings of characters, or the Gromov–Hausdorff distance between metric spaces themselves).

Definition

Formally, a metric space is an ordered pair (M, d) where M is a set and d is a metric on M, i.e., a function

$${\displaystyle d\,\colon M\times M\to \mathbb {R} }$$

${\displaystyle x,y,z\in M}$

1. The distance from a point to itself is zero:
   $${\displaystyle d(x,x)=0}$$

   
2. (Positivity) The distance between two distinct points is always positive:
   $${\displaystyle {\text{If }}x\neq y{\text{, then }}d(x,y)>0}$$

   
3. (Symmetry) The distance from x to y is always the same as the distance from y to x:
   $${\displaystyle d(x,y)=d(y,x)}$$

   
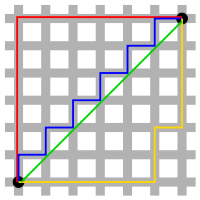
4. The triangle inequality holds:
   $${\displaystyle d(x,z)\leq d(x,y)+d(y,z)}$$

   
   This is a natural property of both physical and metaphorical notions of distance: you can arrive at z from x by taking a detour through y, but this will not make your journey any shorter than the direct path.

If the metric d is unambiguous, one often refers by abuse of notation to "the metric space M".

By taking all axioms except the second, one can show that distance is always non-negative:

$${\displaystyle 0=d(x,x)\leq d(x,y)+d(y,x)=2d(x,y)}$$

${\textstyle {\text{If }}x\neq y{\text{, then }}d(x,y)\neq 0}$