This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (April 2013) (Learn how and when to remove this message)

In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the surface of the figure.^{[further explanation needed]} The same definition extends to any object in ${\displaystyle n}$-dimensional Euclidean space.^[1]

In geometry, one often assumes uniform mass density, in which case the barycenter or center of mass coincides with the centroid. Informally, it can be understood as the point at which a cutout of the shape (with uniformly distributed mass) could be perfectly balanced on the tip of a pin.^[2]

In physics, if variations in gravity are considered, then a center of gravity can be defined as the weighted mean of all points weighted by their specific weight.

In geography, the centroid of a radial projection of a region of the Earth's surface to sea level is the region's geographical center.

History

The term "centroid" is of recent coinage (1814).^[3] It is used as a substitute for the older terms "center of gravity" and "center of mass" when the purely geometrical aspects of that point are to be emphasized. The term is peculiar to the English language; French, for instance, uses "centre de gravité" on most occasions, and other languages use terms of similar meaning.^{[citation needed]}

The center of gravity, as the name indicates, is a notion that arose in mechanics, most likely in connection with building activities. It is uncertain when the idea first appeared, as the concept likely occurred to many people individually with minor differences. Nonetheless, the center of gravity of figures was studied extensively in Antiquity; Bossut credits Archimedes (287–212 BCE) with being the first to find the centroid of plane figures, although he never defines it.^[4] A treatment of centroids of solids by Archimedes has been lost.^[5]

It is unlikely that Archimedes learned the theorem that the medians of a triangle meet in a point—the center of gravity of the triangle—directly from Euclid, as this proposition is not in the Elements. The first explicit statement of this proposition is due to Heron of Alexandria (perhaps the first century CE) and occurs in his Mechanics. It may be added, in passing, that the proposition did not become common in the textbooks on plane geometry until the nineteenth century.^{[citation needed]}

Properties

The geometric centroid of a convex object always lies in the object. A non-convex object might have a centroid that is outside the figure itself. The centroid of a ring or a bowl, for example, lies in the object's central void.

If the centroid is defined, it is a fixed point of all isometries in its symmetry group. In particular, the geometric centroid of an object lies in the intersection of all its hyperplanes of symmetry. The centroid of many figures (regular polygon, regular polyhedron, cylinder, rectangle, rhombus, circle, sphere, ellipse, ellipsoid, superellipse, superellipsoid, etc.) can be determined by this principle alone.

In particular, the centroid of a parallelogram is the meeting point of its two diagonals. This is not true of other quadrilaterals.

For the same reason, the centroid of an object with translational symmetry is undefined (or lies outside the enclosing space), because a translation has no fixed point.

Examples

The centroid of a triangle is the intersection of the three medians of the triangle (each median connecting a vertex with the midpoint of the opposite side).^[6]

For other properties of a triangle's centroid, see below.

Determination

Plumb line method

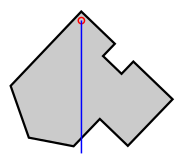
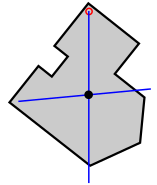
The centroid of a uniformly dense planar lamina, such as in figure (a) below, may be determined experimentally by using a plumbline and a pin to find the collocated center of mass of a thin body of uniform density having the same shape. The body is held by the pin, inserted at a point, off the presumed centroid in such a way that it can freely rotate around the pin; the plumb line is then dropped from the pin (figure b). The position of the plumbline is traced on the surface, and the procedure is repeated with the pin inserted at any different point (or a number of points) off the centroid of the object. The unique intersection point of these lines will be the centroid (figure c). Provided that the body is of uniform density, all lines made this way will include the centroid, and all lines will cross at exactly the same place.

(a)	(b)	(c)

This method can be extended (in theory) to concave shapes where the centroid may lie outside the shape, and virtually to solids (again, of uniform density), where the centroid may lie within the body. The (virtual) positions of the plumb lines need to be recorded by means other than by drawing them along the shape.

Balancing method

For convex two-dimensional shapes, the centroid can be found by balancing the shape on a smaller shape, such as the top of a narrow cylinder. The centroid occurs somewhere within the range of contact between the two shapes (and exactly at the point where the shape would balance on a pin). In principle, progressively narrower cylinders can be used to find the centroid to arbitrary precision. In practice air currents make this infeasible. However, by marking the overlap range from multiple balances, one can achieve a considerable level of accuracy.

Of a finite set of points

The centroid of a finite set of ${\displaystyle k}$ points ${\displaystyle \mathbf {x} _{1},\mathbf {x} _{2},\ldots ,\mathbf {x} _{k}}$ in ${\displaystyle \mathbb {R} ^{n}}$ is^[1]

$${\displaystyle \mathbf {C} ={\frac {\mathbf {x} _{1}+\mathbf {x} _{2}+\cdots +\mathbf {x} _{k}}{k}}.}$$

By geometric decomposition

The centroid of a plane figure ${\displaystyle X}$ can be computed by dividing it into a finite number of simpler figures ${\displaystyle X_{1},X_{2},\dots ,X_{n},}$ computing the centroid ${\displaystyle C_{i}}$ and area ${\displaystyle A_{i}}$ of each part, and then computing

$${\displaystyle C_{x}={\frac {\sum _{i}{C_{i}}_{x}A_{i}}{\sum _{i}A_{i}}},\quad C_{y}={\frac {\sum _{i}{C_{i}}_{y}A_{i}}{\sum _{i}A_{i}}}.}$$

Holes in the figure ${\displaystyle X,}$ overlaps between the parts, or parts that extend outside the figure can all be handled using negative areas ${\displaystyle A_{i}.}$ Namely, the measures ${\displaystyle A_{i}}$ should be taken with positive and negative signs in such a way that the sum of the signs of ${\displaystyle A_{i}}$ for all parts that enclose a given point ${\displaystyle p}$ is ${\displaystyle 1}$ if ${\displaystyle p}$ belongs to ${\displaystyle X,}$ and ${\displaystyle 0}$ otherwise.

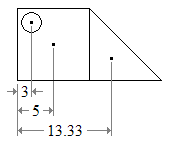
For example, the figure below (a) is easily divided into a square and a triangle, both with positive area; and a circular hole, with negative area (b).

(a) 2D Object

(b) Object described using simpler elements

(c) Centroids of elements of the object

The centroid of each part can be found in any list of centroids of simple shapes (c). Then the centroid of the figure is the weighted average of the three points. The horizontal position of the centroid, from the left edge of the figure is

$${\displaystyle x={\frac {5\times 10^{2}+13.33\times {\frac {1}{2}}10^{2}-3\times \pi 2.5^{2}}{10^{2}+{\frac {1}{2}}10^{2}-\pi 2.5^{2}}}\approx 8.5{\text{ units}}.}$$

The same formula holds for any three-dimensional objects, except that each ${\displaystyle A_{i}}$ should be the volume of ${\displaystyle X_{i},}$ rather than its area. It also holds for any subset of ${\displaystyle \mathbb {R} ^{d},}$Zdroj:https://en.wikipedia.org?pojem=Geometric_center
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.