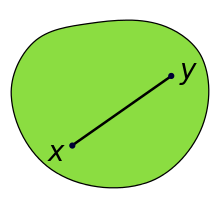
In geometry, a subset of a Euclidean space, or more generally an affine space over the reals, is convex if, given any two points in the subset, the subset contains the whole line segment that joins them. Equivalently, a convex set or a convex region is a subset that intersects every line into a single line segment (possibly empty).^[1][2] For example, a solid cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex.

The boundary of a convex set in the plane is always a convex curve. The intersection of all the convex sets that contain a given subset A of Euclidean space is called the convex hull of A. It is the smallest convex set containing A.

A convex function is a real-valued function defined on an interval with the property that its epigraph (the set of points on or above the graph of the function) is a convex set. Convex minimization is a subfield of optimization that studies the problem of minimizing convex functions over convex sets. The branch of mathematics devoted to the study of properties of convex sets and convex functions is called convex analysis.

The notion of a convex set can be generalized as described below.

Definitions

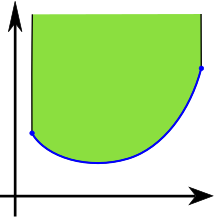
Let S be a vector space or an affine space over the real numbers, or, more generally, over some ordered field (this includes Euclidean spaces, which are affine spaces). A subset C of S is convex if, for all x and y in C, the line segment connecting x and y is included in C.

This means that the affine combination (1 − t)x + ty belongs to C for all x,y in C and t in the interval . This implies that convexity is invariant under affine transformations. Further, it implies that a convex set in a real or complex topological vector space is path-connected (and therefore also connected).

A set C is strictly convex if every point on the line segment connecting x and y other than the endpoints is inside the topological interior of C. A closed convex subset is strictly convex if and only if every one of its boundary points is an extreme point.^[3]

A set C is absolutely convex if it is convex and balanced.

Examples

The convex subsets of R (the set of real numbers) are the intervals and the points of R. Some examples of convex subsets of the Euclidean plane are solid regular polygons, solid triangles, and intersections of solid triangles. Some examples of convex subsets of a Euclidean 3-dimensional space are the Archimedean solids and the Platonic solids. The Kepler-Poinsot polyhedra are examples of non-convex sets.

Non-convex set

A set that is not convex is called a non-convex set. A polygon that is not a convex polygon is sometimes called a concave polygon,^[4] and some sources more generally use the term concave set to mean a non-convex set,^[5] but most authorities prohibit this usage.^[6][7]

The complement of a convex set, such as the epigraph of a concave function, is sometimes called a reverse convex set, especially in the context of mathematical optimization.^[8]

Properties

Given r points u₁, ..., u_r in a convex set S, and r nonnegative numbers λ₁, ..., λ_r such that λ₁ + ... + λ_r = 1, the affine combination

belongs to S. As the definition of a convex set is the case r = 2, this property characterizes convex sets.

Such an affine combination is called a convex combination of u₁, ..., u_r.

Intersections and unions

The collection of convex subsets of a vector space, an affine space, or a Euclidean space has the following properties:^[9][10]

1. The empty set and the whole space are convex.
2. The intersection of any collection of convex sets is convex.
3. The union of a sequence of convex sets is convex, if they form a non-decreasing chain for inclusion. For this property, the restriction to chains is important, as the union of two convex sets need not be convex.

Closed convex sets

Closed convex sets are convex sets that contain all their limit points. They can be characterised as the intersections of closed half-spaces (sets of point in space that lie on and to one side of a hyperplane).

From what has just been said, it is clear that such intersections are convex, and they will also be closed sets. To prove the converse, i.e., every closed convex set may be represented as such intersection, one needs the supporting hyperplane theorem in the form that for a given closed convex set C and point P outside it, there is a closed half-space H that contains C and not P. The supporting hyperplane theorem is a special case of the Hahn–Banach theorem of functional analysis.

Convex sets and rectangles

Let C be a convex body in the plane (a convex set whose interior is non-empty). We can inscribe a rectangle r in C such that a homothetic copy R of r is circumscribed about C. The positive homothety ratio is at most 2 and:^[11]

Blaschke-Santaló diagrams

The set ${\displaystyle {\mathcal {K}}^{2}}$ of all planar convex bodies can be parameterized in terms of the convex body diameter D, its inradius r (the biggest circle contained in the convex body) and its circumradius R (the smallest circle containing the convex body). In fact, this set can be described by the set of inequalities given by^[12][13]

and can be visualized as the image of the function g that maps a convex body to the R² point given by (r/R, D/2R). The image of this function is known a (r, D, R) Blachke-Santaló diagram.^[13]

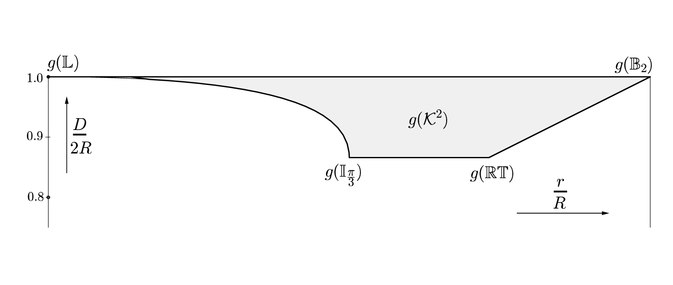
Alternatively, the set ${\displaystyle {\mathcal {K}}^{2}}$ can also be parametrized by its width (the smallest distance between any two different parallel support hyperplanes), perimeter and area.^[12][13]

Other properties

Let X be a topological vector space and ${\displaystyle C\subseteq X}$ be convex.

• ${\displaystyle \operatorname {Cl} C}$ and ${\displaystyle \operatorname {Int} C}$ are both convex (i.e. the closure and interior of convex sets are convex).
• If ${\displaystyle a\in \operatorname {Int} C}$ and ${\displaystyle b\in \operatorname {Cl} C}$ then ${\displaystyle a,b\,\subseteq \operatorname {Int} C}$ (where ${\displaystyle a,b\,:=\left\{(1-r)a+rb:0\leq r<1\right\}}$).
• If ${\displaystyle \operatorname {Int} C\neq \emptyset }$ then:
  • ${\displaystyle \operatorname {cl} \left(\operatorname {Int} C\right)=\operatorname {Cl} C}$, and
  • ${\displaystyle \operatorname {Int} C=\operatorname {Int} \left(\operatorname {Cl} C\right)=C^{i}}$, where ${\displaystyle C^{i}}$ is the algebraic interior of C.

Convex hulls and Minkowski sumsedit

Convex hullsedit

Every subset A of the vector space is contained within a smallest convex set (called the convex hull of A), namely the intersection of all convex sets containing A. The convex-hull operator Conv() has the characteristic properties of a hull operator:

• extensive: S ⊆ Conv(S),
• non-decreasing: S ⊆ T implies that Conv(S) ⊆ Conv(T), and
• idempotent: Conv(Conv(S)) = Conv(S).

The convex-hull operation is needed for the set of convex sets to form a lattice, in which the "join" operation is the convex hull of the union of two convex sets

The intersection of any collection of convex sets is itself convex, so the convex subsets of a (real or complex) vector space form a complete lattice.

Minkowski additionedit

In a real vector-space, the Minkowski sum of two (non-empty) sets, S₁ and S₂, is defined to be the set S₁ + S₂ formed by the addition of vectors element-wise from the summand-sets