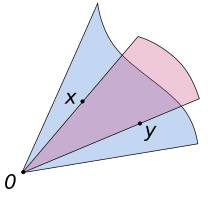
In linear algebra, a cone—sometimes called a linear cone for distinguishing it from other sorts of cones—is a subset of a vector space that is closed under positive scalar multiplication; that is, C is a cone if ${\displaystyle x\in C}$ implies ${\displaystyle sx\in C}$ for every positive scalar s. A cone need not be convex, or even look like a cone in Euclidean space.

When the scalars are real numbers, or belong to an ordered field, one generally calls a cone a subset of a vector space that is closed under multiplication by a positive scalar. In this context, a convex cone is a cone that is closed under addition, or, equivalently, a subset of a vector space that is closed under linear combinations with positive coefficients. It follows that convex cones are convex sets.^[1]

In this article, only the case of scalars in an ordered field is considered.

Definition

A subset C of a vector space V over an ordered field F is a cone (or sometimes called a linear cone) if for each x in C and positive scalar α in F, the product αx is in C.^[2] Note that some authors define cone with the scalar α ranging over all non-negative scalars (rather than all positive scalars, which does not include 0).^[3]

A cone C is a convex cone if αx + βy belongs to C, for any positive scalars α, β, and any x, y in C.^[4][5] A cone C is convex if and only if C + C ⊆ C.

This concept is meaningful for any vector space that allows the concept of "positive" scalar, such as spaces over the rational, algebraic, or (more commonly) the real numbers. Also note that the scalars in the definition are positive meaning that the origin does not have to belong to C. Some authors use a definition that ensures the origin belongs to C.^[6] Because of the scaling parameters α and β, cones are infinite in extent and not bounded.

If C is a convex cone, then for any positive scalar α and any x in C the vector ${\displaystyle \alpha x={\tfrac {\alpha }{2}}x+{\tfrac {\alpha }{2}}x\in C.}$ It follows that a convex cone C is a special case of a linear cone.

It follows from the above property that a convex cone can also be defined as a linear cone that is closed under convex combinations, or just under additions. More succinctly, a set C is a convex cone if and only if αC = C and C + C = C, for any positive scalar α.

Examples

• For a vector space V, the empty set, the space V, and any linear subspace of V are convex cones.
• The conical hull of a finite or infinite set of vectors in ${\displaystyle \mathbb {R} ^{n}}$ is a convex cone.
• The tangent cones of a convex set are convex cones.
• The set
  $${\displaystyle \left\{x\in \mathbb {R} ^{2}\mid x_{2}\geq 0,x_{1}=0\right\}\cup \left\{x\in \mathbb {R} ^{2}\mid x_{1}\geq 0,x_{2}=0\right\}}$$

  
  is a cone but not a convex cone.
• The norm cone
  $${\displaystyle \left\{(x,r)\in \mathbb {R} ^{d+1}\mid \|x\|\leq r\right\}}$$

  
  is a convex cone.
• The intersection of two convex cones in the same vector space is again a convex cone, but their union may fail to be one.
• The class of convex cones is also closed under arbitrary linear maps. In particular, if C is a convex cone, so is its opposite ${\displaystyle -C}$ and ${\displaystyle C\cap -C}$ is the largest linear subspace contained in C.
• The set of positive semidefinite matrices.
• The set of nonnegative continuous functions is a convex cone.

Special examples

Affine convex cones

An affine convex cone is the set resulting from applying an affine transformation to a convex cone.^[7] A common example is translating a convex cone by a point p: p + C. Technically, such transformations can produce non-cones. For example, unless p = 0, p + C is not a linear cone. However, it is still called an affine convex cone.

Half-spaces

A (linear) hyperplane is a set in the form ${\displaystyle \{x\in V\mid f(x)=c\}}$ where f is a linear functional on the vector space V. A closed half-space is a set in the form ${\displaystyle \{x\in V\mid f(x)\leq c\}}$ or ${\displaystyle \{x\in V\mid f(x)\geq c\},}$ and likewise an open half-space uses strict inequality.^[8][9]

Half-spaces (open or closed) are affine convex cones. Moreover (in finite dimensions), any convex cone C that is not the whole space V must be contained in some closed half-space H of V; this is a special case of Farkas' lemma.

Polyhedral and finitely generated cones

Polyhedral cones are special kinds of cones that can be defined in several ways:^{[10]: 256–257}

• A cone C is polyhedral if it is the conical hull of finitely many vectors (this property is also called finitely-generated).^[11][12] I.e., there is a set of vectors ${\displaystyle \{v_{1},\ldots ,v_{k}\}}$ so that ${\displaystyle C=\{a_{1}v_{1}+\cdots +a_{k}v_{k}\mid a_{i}\in \mathbb {R} _{\geq 0},v_{i}\in \mathbb {R} ^{n}\}}$.
• A cone is polyhedral if it is the intersection of a finite number of half-spaces which have 0 on their boundary (this was proved by Weyl in 1935).
• A cone C is polyhedral if there is some matrix ${\displaystyle A}$ such that ${\displaystyle C=\{x\in \mathbb {R} ^{n}\mid Ax\geq 0\}}$.
• A cone is polyhedral if it is the solution set of a system of homogeneous linear inequalities. Algebraically, each inequality is defined by a row of the matrix A. Geometrically, each inequality defines a halfspace that passes through the origin.

Every finitely generated cone is a polyhedral cone, and every polyhedral cone is a finitely generated cone.^[11] Every polyhedral cone has a unique representation as a conical hull of its extremal generators, and a unique representation of intersections of halfspaces, given each linear form associated with the halfspaces also define a support hyperplane of a facet.^[13]

Polyhedral cones play a central role in the representation theory of polyhedra. For instance, the decomposition theorem for polyhedra states that every polyhedron can be written as the Minkowski sum of a convex polytope and a polyhedral cone.^[14][15] Polyhedral cones also play an important part in proving the related Finite Basis Theorem for polytopes which shows that every polytope is a polyhedron and every bounded polyhedron is a polytope.^[14][16][17]

The two representations of a polyhedral cone - by inequalities and by vectors - may have very different sizes. For example, consider the cone of all non-negative n-by-n matrices with equal row and column sums. The inequality representation requires n² inequalities and 2(n − 1) equations, but the vector representation requires n! vectors (see the Birkhoff-von Neumann Theorem). The opposite can also happen - the number of vectors may be polynomial while the number of inequalities is exponential.^[10]: 256

The two representations together provide an efficient way to decide whether a given vector is in the cone: to show that it is in the cone, it is sufficient to present it as a conic combination of the defining vectors; to show that it is not in the cone, it is sufficient to present a single defining inequality that it violates. This fact is known as Farkas' lemma.

A subtle point in the representation by vectors is that the number of vectors may be exponential in the dimension, so the proof that a vector is in the cone might be exponentially long. Fortunately, Carathéodory's theorem guarantees that every vector in the cone can be represented by at most d defining vectors, where d is the dimension of the space.

Blunt, pointed, flat, salient, and proper cones

According to the above definition, if C is a convex cone, then C ∪ {0} is a convex cone, too. A convex cone is said to be pointed if 0 is in C, and blunt if 0 is not in C.^[2][18] Blunt cones can be excluded from the definition of convex cone by substituting "non-negative" for "positive" in the condition of α, β.

A cone is called flat if it contains some nonzero vector x and its opposite −x, meaning C contains a linear subspace of dimension at least one, and salient otherwise.^[19][20] A blunt convex cone is necessarily salient, but the converse is not necessarily true. A convex cone C is salient if and only if C ∩ −C ⊆ {0}. A cone C is said to be generating if ${\displaystyle C-C=\{x-y\mid x\in C,y\in C\}}$ equals the whole vector space.^[21]

Some authors require salient cones to be pointed.^[22] The term "pointed" is also often used to refer to a closed cone that contains no complete line (i.e., no nontrivial subspace of the ambient vector space V, or what is called a salient cone).^[23][24][25] The term proper (convex) cone is variously defined, depending on the context and author. It often means a cone that satisfies other properties like being convex, closed, pointed, salient, and full-dimensional.^[26][27][28] Because of these varying definitions, the context or source should be consulted for the definition of these terms.

Rational cones

A type of cone of particular interest to pure mathematicians is the partially ordered set of rational cones. "Rational cones are important objects in toric algebraic geometry, combinatorial commutative algebra, geometric combinatorics, integer programming.".^[29] This object arises when we study cones in ${\displaystyle \mathbb {R} ^{d}}$ together with the lattice ${\displaystyle \mathbb {Z} ^{d}}$. A cone is called rational (here we assume "pointed", as defined above) whenever its generators all have integer coordinates, i.e., if ${\displaystyle C}$ is a rational cone, then ${\displaystyle C=\{a_{1}v_{1}+\cdots +a_{k}v_{k}\mid a_{i}\in \mathbb {R} _{+},v_{i}\in \mathbb {Z} ^{d}\}}$.

Dual cone

Let C ⊂ V be a set, not necessarily a convex set, in a real vector space V equipped with an inner product. The (continuous or topological) dual cone to C is the set

${\displaystyle C^{*}=\{v\in V\mid \forall w\in C,\langle w,v\rangle \geq 0\},}$

which is always a convex cone. Here, ${\displaystyle \langle w,v\rangle }$ is the duality pairing between C and V, i.e. ${\displaystyle \langle w,v\rangle =v(w)}$.

More generally, the (algebraic) dual cone to C ⊂ V in a linear space V is a subset of the dual space V* defined by:

${\displaystyle C^{\ast <!--\; \ast \; -->}}$Zdroj:https://en.wikipedia.org?pojem=Convex_cone
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---