In electrical engineering, a transmission line is a specialized cable or other structure designed to conduct electromagnetic waves in a contained manner. The term applies when the conductors are long enough that the wave nature of the transmission must be taken into account. This applies especially to radio-frequency engineering because the short wavelengths mean that wave phenomena arise over very short distances (this can be as short as millimetres depending on frequency). However, the theory of transmission lines was historically developed to explain phenomena on very long telegraph lines, especially submarine telegraph cables.

Transmission lines are used for purposes such as connecting radio transmitters and receivers with their antennas (they are then called feed lines or feeders), distributing cable television signals, trunklines routing calls between telephone switching centres, computer network connections and high speed computer data buses. RF engineers commonly use short pieces of transmission line, usually in the form of printed planar transmission lines, arranged in certain patterns to build circuits such as filters. These circuits, known as distributed-element circuits, are an alternative to traditional circuits using discrete capacitors and inductors.

Overview

Ordinary electrical cables suffice to carry low frequency alternating current (AC), such as mains power, which reverses direction 100 to 120 times per second, and audio signals. However, they are not generally used to carry currents in the radio frequency range,^[1] above about 30 kHz, because the energy tends to radiate off the cable as radio waves, causing power losses. Radio frequency currents also tend to reflect from discontinuities in the cable such as connectors and joints, and travel back down the cable toward the source.^[1][2] These reflections act as bottlenecks, preventing the signal power from reaching the destination. Transmission lines use specialized construction, and impedance matching, to carry electromagnetic signals with minimal reflections and power losses. The distinguishing feature of most transmission lines is that they have uniform cross sectional dimensions along their length, giving them a uniform impedance, called the characteristic impedance,^[2][3][4] to prevent reflections. Types of transmission line include parallel line (ladder line, twisted pair), coaxial cable, and planar transmission lines such as stripline and microstrip.^[5][6] The higher the frequency of electromagnetic waves moving through a given cable or medium, the shorter the wavelength of the waves. Transmission lines become necessary when the transmitted frequency's wavelength is sufficiently short that the length of the cable becomes a significant part of a wavelength.

At microwave frequencies and above, power losses in transmission lines become excessive, and waveguides are used instead,^[1] which function as "pipes" to confine and guide the electromagnetic waves.^[6] Some sources define waveguides as a type of transmission line;^[6] however, this article will not include them.

History

Mathematical analysis of the behaviour of electrical transmission lines grew out of the work of James Clerk Maxwell, Lord Kelvin, and Oliver Heaviside. In 1855, Lord Kelvin formulated a diffusion model of the current in a submarine cable. The model correctly predicted the poor performance of the 1858 trans-Atlantic submarine telegraph cable. In 1885, Heaviside published the first papers that described his analysis of propagation in cables and the modern form of the telegrapher's equations.^[7]

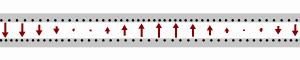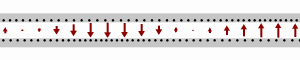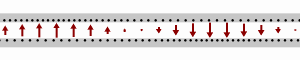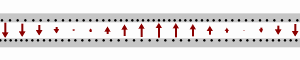
The four terminal model

For the purposes of analysis, an electrical transmission line can be modelled as a two-port network (also called a quadripole), as follows:

In the simplest case, the network is assumed to be linear (i.e. the complex voltage across either port is proportional to the complex current flowing into it when there are no reflections), and the two ports are assumed to be interchangeable. If the transmission line is uniform along its length, then its behaviour is largely described by a two parameters called characteristic impedance, symbol Z₀ and propagation delay, symbol ${\displaystyle \tau _{p}}$. Z₀ is the ratio of the complex voltage of a given wave to the complex current of the same wave at any point on the line. Typical values of Z₀ are 50 or 75 ohms for a coaxial cable, about 100 ohms for a twisted pair of wires, and about 300 ohms for a common type of untwisted pair used in radio transmission. Propagation delay is proportional to the length of the transmission line and is never less than the length divided by the speed of light. Typical delays for modern communication transmission lines vary from 3.33 ns/m to 5 ns/m.

When sending power down a transmission line, it is usually desirable that as much power as possible will be absorbed by the load and as little as possible will be reflected back to the source. This can be ensured by making the load impedance equal to Z₀, in which case the transmission line is said to be matched.

Some of the power that is fed into a transmission line is lost because of its resistance. This effect is called ohmic or resistive loss (see ohmic heating). At high frequencies, another effect called dielectric loss becomes significant, adding to the losses caused by resistance. Dielectric loss is caused when the insulating material inside the transmission line absorbs energy from the alternating electric field and converts it to heat (see dielectric heating). The transmission line is modelled with a resistance (R) and inductance (L) in series with a capacitance (C) and conductance (G) in parallel. The resistance and conductance contribute to the loss in a transmission line.

The total loss of power in a transmission line is often specified in decibels per metre (dB/m), and usually depends on the frequency of the signal. The manufacturer often supplies a chart showing the loss in dB/m at a range of frequencies. A loss of 3 dB corresponds approximately to a halving of the power.

Propagation delay is often specified in units of nanoseconds per metre. While propagation delay usually depends on the frequency of the signal, transmission lines are typically operated over frequency ranges where the propagation delay is approximately constant.

Telegrapher's equations

The telegrapher's equations (or just telegraph equations) are a pair of linear differential equations which describe the voltage (${\displaystyle V}$) and current (${\displaystyle I}$) on an electrical transmission line with distance and time. They were developed by Oliver Heaviside who created the transmission line model, and are based on Maxwell's equations.

The transmission line model is an example of the distributed-element model. It represents the transmission line as an infinite series of two-port elementary components, each representing an infinitesimally short segment of the transmission line:

• The distributed resistance ${\displaystyle R}$ of the conductors is represented by a series resistor (expressed in ohms per unit length).
• The distributed inductance ${\displaystyle L}$ (due to the magnetic field around the wires, self-inductance, etc.) is represented by a series inductor (in henries per unit length).
• The capacitance ${\displaystyle C}$ between the two conductors is represented by a shunt capacitor (in farads per unit length).
• The conductance ${\displaystyle G}$ of the dielectric material separating the two conductors is represented by a shunt resistor between the signal wire and the return wire (in siemens per unit length).

The model consists of an infinite series of the elements shown in the figure, and the values of the components are specified per unit length so the picture of the component can be misleading. ${\displaystyle R}$, ${\displaystyle L}$, ${\displaystyle C}$, and ${\displaystyle G}$ may also be functions of frequency. An alternative notation is to use ${\displaystyle R'}$, ${\displaystyle L'}$, ${\displaystyle C'}$ and ${\displaystyle G'}$ to emphasize that the values are derivatives with respect to length. These quantities can also be known as the primary line constants to distinguish from the secondary line constants derived from them, these being the propagation constant, attenuation constant and phase constant.

The line voltage ${\displaystyle V(x)}$ and the current ${\displaystyle I(x)}$ can be expressed in the frequency domain as

${\displaystyle {\frac {\partial V(x)}{\partial x}}=-(R+j\,\omega \,L)\,I(x)}$

${\displaystyle \frac{\mathrm{\partial <!--\; \partial \; -->}I(x)}{\mathrm{\partial <!--\; \partial \; -->}x}=-<!--\; -\; -->(G+j\mathrm{\omega <!--\; \omega \; -->}C}$Zdroj:https://en.wikipedia.org?pojem=Balanced_transmission_line
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---