Molecular dynamics (MD) is a computer simulation method for analyzing the physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a fixed period of time, giving a view of the dynamic "evolution" of the system. In the most common version, the trajectories of atoms and molecules are determined by numerically solving Newton's equations of motion for a system of interacting particles, where forces between the particles and their potential energies are often calculated using interatomic potentials or molecular mechanical force fields. The method is applied mostly in chemical physics, materials science, and biophysics.

Because molecular systems typically consist of a vast number of particles, it is impossible to determine the properties of such complex systems analytically; MD simulation circumvents this problem by using numerical methods. However, long MD simulations are mathematically ill-conditioned, generating cumulative errors in numerical integration that can be minimized with proper selection of algorithms and parameters, but not eliminated.

For systems that obey the ergodic hypothesis, the evolution of one molecular dynamics simulation may be used to determine the macroscopic thermodynamic properties of the system: the time averages of an ergodic system correspond to microcanonical ensemble averages. MD has also been termed "statistical mechanics by numbers" and "Laplace's vision of Newtonian mechanics" of predicting the future by animating nature's forces^[1] and allowing insight into molecular motion on an atomic scale.

History

MD was originally developed in the early 1950s, following earlier successes with Monte Carlo simulations—which themselves date back to the eighteenth century, in the Buffon's needle problem for example—but was popularized for statistical mechanics at Los Alamos National Laboratory by Marshall Rosenbluth and Nicholas Metropolis in what is known today as the Metropolis–Hastings algorithm. Interest in the time evolution of N-body systems dates much earlier to the seventeenth century, beginning with Isaac Newton, and continued into the following century largely with a focus on celestial mechanics and issues such as the stability of the solar system. Many of the numerical methods used today were developed during this time period, which predates the use of computers; for example, the most common integration algorithm used today, the Verlet integration algorithm, was used as early as 1791 by Jean Baptiste Joseph Delambre. Numerical calculations with these algorithms can be considered to be MD done "by hand".

As early as 1941, integration of the many-body equations of motion was carried out with analog computers. Some undertook the labor-intensive work of modeling atomic motion by constructing physical models, e.g., using macroscopic spheres. The aim was to arrange them in such a way as to replicate the structure of a liquid and use this to examine its behavior. J.D. Bernal describes this process in 1962, writing:^[2]

... I took a number of rubber balls and stuck them together with rods of a selection of different lengths ranging from 2.75 to 4 inches. I tried to do this in the first place as casually as possible, working in my own office, being interrupted every five minutes or so and not remembering what I had done before the interruption.

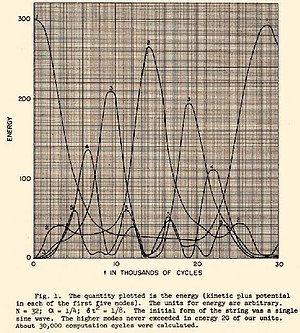
Following the discovery of microscopic particles and the development of computers, interest expanded beyond the proving ground of gravitational systems to the statistical properties of matter. In an attempt to understand the origin of irreversibility, Enrico Fermi proposed in 1953, and published in 1955,^[3] the use of the early computer MANIAC I, also at Los Alamos National Laboratory, to solve the time evolution of the equations of motion for a many-body system subject to several choices of force laws. Today, this seminal work is known as the Fermi–Pasta–Ulam–Tsingou problem. The time evolution of the energy from the original work is shown in the figure to the right.

In 1957, Berni Alder and Thomas Wainwright used an IBM 704 computer to simulate perfectly elastic collisions between hard spheres.^[4] In 1960, in perhaps the first realistic simulation of matter, J.B. Gibson et al. simulated radiation damage of solid copper by using a Born–Mayer type of repulsive interaction along with a cohesive surface force.^[5] In 1964, Aneesur Rahman published simulations of liquid argon that used a Lennard-Jones potential; calculations of system properties, such as the coefficient of self-diffusion, compared well with experimental data.^[6] Today, the Lennard-Jones potential is still one of the most frequently used intermolecular potentials.^[7][8] It is used for describing simple substances (a.k.a. Lennard-Jonesium^[9][10][11]) for conceptual and model studies and as a building block in many force fields of real substances.^[12][13]

Areas of application and limits

First used in theoretical physics, the molecular dynamics method gained popularity in materials science soon afterward, and since the 1970s it has also been commonly used in biochemistry and biophysics. MD is frequently used to refine 3-dimensional structures of proteins and other macromolecules based on experimental constraints from X-ray crystallography or NMR spectroscopy. In physics, MD is used to examine the dynamics of atomic-level phenomena that cannot be observed directly, such as thin film growth and ion subplantation, and to examine the physical properties of nanotechnological devices that have not or cannot yet be created. In biophysics and structural biology, the method is frequently applied to study the motions of macromolecules such as proteins and nucleic acids, which can be useful for interpreting the results of certain biophysical experiments and for modeling interactions with other molecules, as in ligand docking. In principle, MD can be used for ab initio prediction of protein structure by simulating folding of the polypeptide chain from a random coil.

The results of MD simulations can be tested through comparison to experiments that measure molecular dynamics, of which a popular method is NMR spectroscopy. MD-derived structure predictions can be tested through community-wide experiments in Critical Assessment of Protein Structure Prediction (CASP), although the method has historically had limited success in this area. Michael Levitt, who shared the Nobel Prize partly for the application of MD to proteins, wrote in 1999 that CASP participants usually did not use the method due to "... a central embarrassment of molecular mechanics, namely that energy minimization or molecular dynamics generally leads to a model that is less like the experimental structure".^[14] Improvements in computational resources permitting more and longer MD trajectories, combined with modern improvements in the quality of force field parameters, have yielded some improvements in both structure prediction and homology model refinement, without reaching the point of practical utility in these areas; many identify force field parameters as a key area for further development.^[15][16][17]

MD simulation has been reported for pharmacophore development and drug design.^[18] For example, Pinto et al. implemented MD simulations of Bcl-xL complexes to calculate average positions of critical amino acids involved in ligand binding.^[19] Carlson et al. implemented molecular dynamics simulations to identify compounds that complement a receptor while causing minimal disruption to the conformation and flexibility of the active site. Snapshots of the protein at constant time intervals during the simulation were overlaid to identify conserved binding regions (conserved in at least three out of eleven frames) for pharmacophore development. Spyrakis et al. relied on a workflow of MD simulations, fingerprints for ligands and proteins (FLAP) and linear discriminant analysis (LDA) to identify the best ligand-protein conformations to act as pharmacophore templates based on retrospective ROC analysis of the resulting pharmacophores. In an attempt to ameliorate structure-based drug discovery modeling, vis-à-vis the need for many modeled compounds, Hatmal et al. proposed a combination of MD simulation and ligand-receptor intermolecular contacts analysis to discern critical intermolecular contacts (binding interactions) from redundant ones in a single ligand–protein complex. Critical contacts can then be converted into pharmacophore models that can be used for virtual screening.^[20]

An important factor is intramolecular hydrogen bonds,^[21] which are not explicitly included in modern force fields, but described as Coulomb interactions of atomic point charges.^{[citation needed]} This is a crude approximation because hydrogen bonds have a partially quantum mechanical and chemical nature. Furthermore, electrostatic interactions are usually calculated using the dielectric constant of a vacuum, even though the surrounding aqueous solution has a much higher dielectric constant. Thus, using the macroscopic dielectric constant at short interatomic distances is questionable. Finally, van der Waals interactions in MD are usually described by Lennard-Jones potentials based on the Fritz London theory that is only applicable in a vacuum.^{[citation needed]} However, all types of van der Waals forces are ultimately of electrostatic origin and therefore depend on dielectric properties of the environment.^[22] The direct measurement of attraction forces between different materials (as Hamaker constant) shows that "the interaction between hydrocarbons across water is about 10% of that across vacuum".^[22] The environment-dependence of van der Waals forces is neglected in standard simulations, but can be included by developing polarizable force fields.

Design constraints

The design of a molecular dynamics simulation should account for the available computational power. Simulation size (n = number of particles), timestep, and total time duration must be selected so that the calculation can finish within a reasonable time period. However, the simulations should be long enough to be relevant to the time scales of the natural processes being studied. To make statistically valid conclusions from the simulations, the time span simulated should match the kinetics of the natural process. Otherwise, it is analogous to making conclusions about how a human walks when only looking at less than one footstep. Most scientific publications about the dynamics of proteins and DNA^[23][24] use data from simulations spanning nanoseconds (10⁻⁹ s) to microseconds (10⁻⁶ s). To obtain these simulations, several CPU-days to CPU-years are needed. Parallel algorithms allow the load to be distributed among CPUs; an example is the spatial or force decomposition algorithm.^[25]

During a classical MD simulation, the most CPU intensive task is the evaluation of the potential as a function of the particles' internal coordinates. Within that energy evaluation, the most expensive one is the non-bonded or non-covalent part. In big O notation, common molecular dynamics simulations scale by ${\displaystyle O(n^{2})}$ if all pair-wise electrostatic and van der Waals interactions must be accounted for explicitly. This computational cost can be reduced by employing electrostatics methods such as particle mesh Ewald summation ( ${\displaystyle O(n\log(n))}$ ), particle-particle-particle mesh (P³M), or good spherical cutoff methods ( ${\displaystyle O(n)}$ ). ^{[citation needed]}

Another factor that impacts total CPU time needed by a simulation is the size of the integration timestep. This is the time length between evaluations of the potential. The timestep must be chosen small enough to avoid discretization errors (i.e., smaller than the period related to fastest vibrational frequency in the system). Typical timesteps for classical MD are on the order of 1 femtosecond (10⁻¹⁵ s). This value may be extended by using algorithms such as the SHAKE constraint algorithm, which fix the vibrations of the fastest atoms (e.g., hydrogens) into place. Multiple time scale methods have also been developed, which allow extended times between updates of slower long-range forces.^[26][27][28]

For simulating molecules in a solvent, a choice should be made between an explicit and implicit solvent. Explicit solvent particles (such as the TIP3P, SPC/E and SPC-f water models) must be calculated expensively by the force field, while implicit solvents use a mean-field approach. Using an explicit solvent is computationally expensive, requiring inclusion of roughly ten times more particles in the simulation. But the granularity and viscosity of explicit solvent is essential to reproduce certain properties of the solute molecules. This is especially important to reproduce chemical kinetics.

In all kinds of molecular dynamics simulations, the simulation box size must be large enough to avoid boundary condition artifacts. Boundary conditions are often treated by choosing fixed values at the edges (which may cause artifacts), or by employing periodic boundary conditions in which one side of the simulation loops back to the opposite side, mimicking a bulk phase (which may cause artifacts too).

Microcanonical ensemble (NVE)

In the microcanonical ensemble, the system is isolated from changes in moles (N), volume (V), and energy (E). It corresponds to an adiabatic process with no heat exchange. A microcanonical molecular dynamics trajectory may be seen as an exchange of potential and kinetic energy, with total energy being conserved. For a system of N particles with coordinates ${\displaystyle X}$ and velocities ${\displaystyle V}$, the following pair of first order differential equations may be written in Newton's notation as

${\displaystyle F(X)=-\nabla U(X)=M{\dot {V}}(t)}$

${\displaystyle V(t)={\dot {X}}(t).}$

The potential energy function ${\displaystyle U(X)}$ of the system is a function of the particle coordinates ${\displaystyle X}$. It is referred to simply as the potential in physics, or the force field in chemistry. The first equation comes from Newton's laws of motion; the force ${\displaystyle F}$ acting on each particle in the system can be calculated as the negative gradient of ${\displaystyle U(X)}$.

For every time step, each particle's position ${\displaystyle X}$ and velocity ${\displaystyle V}$ may be integrated with a symplectic integrator method such as Verlet integration. The time evolution of ${\displaystyle X}$ and ${\displaystyle V}$ is called a trajectory. Given the initial positions (e.g., from theoretical knowledge) and velocities (e.g., randomized Gaussian), we can calculate all future (or past) positions and velocities.

One frequent source of confusion is the meaning of temperature in MD. Commonly we have experience with macroscopic temperatures, which involve a huge number of particles, but temperature is a statistical quantity. If there is a large enough number of atoms, statistical temperature can be estimated from the instantaneous temperature, which is found by equating the kinetic energy of the system to nk_BT/2, where n is the number of degrees of freedom of the system.

A temperature-related phenomenon arises due to the small number of atoms that are used in MD simulations. For example, consider simulating the growth of a copper film starting with a substrate containing 500 atoms and a deposition energy of 100 eV. In the real world, the 100 eV from the deposited atom would rapidly be transported through and shared among a large number of atoms (${\displaystyle 10^{10}}$ or more) with no big change in temperature. When there are only 500 atoms, however, the substrate is almost immediately vaporized by the deposition. Something similar happens in biophysical simulations. The temperature of the system in NVE is naturally raised when macromolecules such as proteins undergo exothermic conformational changes and binding.

Canonical ensemble (NVT)

In the canonical ensemble, amount of substance (N), volume (V) and temperature (T) are conserved. It is also sometimes called constant temperature molecular dynamics (CTMD). In NVT, the energy of endothermic and exothermic processes is exchanged with a thermostat.

A variety of thermostat algorithms are available to add and remove energy from the boundaries of an MD simulation in a more or less realistic way, approximating the canonical ensemble. Popular methods to control temperature include velocity rescaling, the Nosé–Hoover thermostat, Nosé–Hoover chains, the Berendsen thermostat, the Andersen thermostat and Langevin dynamics. The Berendsen thermostat might introduce the flying ice cube effect, which leads to unphysical translations and rotations of the simulated system.

It is not trivial to obtain a canonical ensemble distribution of conformations and velocities using these algorithms. How this depends on system size, thermostat choice, thermostat parameters, time step and integrator is the subject of many articles in the field.

Isothermal–isobaric (NPT) ensemble

In the isothermal–isobaric ensemble, amount of substance (N), pressure (P) and temperature (T) are conserved. In addition to a thermostat, a barostat is needed. It corresponds most closely to laboratory conditions with a flask open to ambient temperature and pressure.

In the simulation of biological membranes, isotropic pressure control is not appropriate. For lipid bilayers, pressure control occurs under constant membrane area (NPAT) or constant surface tension "gamma" (NPγT).

Generalized ensembles

The replica exchange method is a generalized ensemble. It was originally created to deal with the slow dynamics of disordered spin systems. It is also called parallel tempering. The replica exchange MD (REMD) formulation^[29] tries to overcome the multiple-minima problem by exchanging the temperature of non-interacting replicas of the system running at several temperatures.

Potentials in MD simulations

A molecular dynamics simulation requires the definition of a potential function, or a description of the terms by which the particles in the simulation will interact. In chemistry and biology this is usually referred to as a force field and in materials physics as an interatomic potential. Potentials may be defined at many levels of physical accuracy; those most commonly used in chemistry are based on molecular mechanics and embody a classical mechanics treatment of particle-particle interactions that can reproduce structural and conformational changes but usually cannot reproduce chemical reactions.

The reduction from a fully quantum description to a classical potential entails two main approximations. The first one is the Born–Oppenheimer approximation, which states that the dynamics of electrons are so fast that they can be considered to react instantaneously to the motion of their nuclei. As a consequence, they may be treated separately. The second one treats the nuclei, which are much heavier than electrons, as point particles that follow classical Newtonian dynamics. In classical molecular dynamics, the effect of the electrons is approximated as one potential energy surface, usually representing the ground state.

When finer levels of detail are needed, potentials based on quantum mechanics are used; some methods attempt to create hybrid classical/quantum potentials where the bulk of the system is treated classically but a small region is treated as a quantum system, usually undergoing a chemical transformation.

Empirical potentials

Empirical potentials used in chemistry are frequently called force fields, while those used in materials physics are called interatomic potentials.

Most force fields in chemistry are empirical and consist of a summation of bonded forces associated with chemical bonds, bond angles, and bond dihedrals, and non-bonded forces associated with van der Waals forces and electrostatic charge.^[30] Empirical potentials represent quantum-mechanical effects in a limited way through ad hoc functional approximations. These potentials contain free parameters such as atomic charge, van der Waals parameters reflecting estimates of atomic radius, and equilibrium bond length, angle, and dihedral; these are obtained by fitting against detailed electronic calculations (quantum chemical simulations) or experimental physical properties such as elastic constants, lattice parameters and spectroscopic measurements.

Because of the non-local nature of non-bonded interactions, they involve at least weak interactions between all particles in the system. Its calculation is normally the bottleneck in the speed of MD simulations. To lower the computational cost, force fields employ numerical approximations such as shifted cutoff radii, reaction field algorithms, particle mesh Ewald summation, or the newer particle–particle-particle–mesh (P3M).

Chemistry force fields commonly employ preset bonding arrangements (an exception being ab initio dynamics), and thus are unable to model the process of chemical bond breaking and reactions explicitly. On the other hand, many of the potentials used in physics, such as those based on the bond order formalism can describe several different coordinations of a system and bond breaking.^[31][32] Examples of such potentials include the Brenner potential^[33] for hydrocarbons and its further developments for the C-Si-H^[34] and C-O-H^[35] systems. The ReaxFF potential^[36] can be considered a fully reactive hybrid between bond order potentials and chemistry force fields.

Pair potentials versus many-body potentials

The potential functions representing the non-bonded energy are formulated as a sum over interactions between the particles of the system. The simplest choice, employed in many popular force fields, is the "pair potential", in which the total potential energy can be calculated from the sum of energy contributions between pairs of atoms. Therefore, these force fields are also called "additive force fields". An example of such a pair potential is the non-bonded Lennard-Jones potential (also termed the 6–12 potential), used for calculating van der Waals forces.

${\displaystyle U(r)=4\varepsilon \left}$

Another example is the Born (ionic) model of the ionic lattice. The first term in the next equation is Coulomb's law for a pair of ions, the second term is the short-range repulsion explained by Pauli's exclusion principle and the final term is the dispersion interaction term. Usually, a simulation only includes the dipolar term, although sometimes the quadrupolar term is also included.^[37][38] When n_l = 6, this potential is also called the Coulomb–Buckingham potential.

${\displaystyle U_{ij}(r_{ij})=\frac{z_i{z}_j}{4\mathrm{\pi <!--\; \pi \; -->}{\mathrm{ϵ<!--\; ϵ\; -->}}_0}\frac{1}{r_{ij}}+A_l\exp <!--\; \; -->\frac{-<!--\; -\; -->r_{}}{}}$Zdroj:https://en.wikipedia.org?pojem=Molecular_dynamics
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---