Quantum field theory
Feynman diagram
History
Background Field theory Electromagnetism Weak force Strong force Quantum mechanics Special relativity General relativity Gauge theory Yang–Mills theory
Symmetries Symmetry in quantum mechanics C-symmetry P-symmetry T-symmetry Lorentz symmetry Poincaré symmetry Gauge symmetry Explicit symmetry breaking Spontaneous symmetry breaking Noether charge Topological charge
Tools Anomaly Background field method BRST quantization Correlation function Crossing Effective action Effective field theory Expectation value Feynman diagram Lattice field theory LSZ reduction formula Partition function Propagator Quantization Regularization Renormalization Vacuum state Wick's theorem
Equations Dirac equation Klein–Gordon equation Proca equations Wheeler–DeWitt equation Bargmann–Wigner equations
Standard Model Quantum electrodynamics Electroweak interaction Quantum chromodynamics Higgs mechanism
Incomplete theories String theory Supersymmetry Technicolor Theory of everything Quantum gravity
Scientists Adler Anderson Anselm Bargmann Becchi Belavin Bell Berezin Bethe Bjorken Bleuer Bogoliubov Brodsky Brout Buchholz Cachazo Callan Coleman Dashen DeWitt Dirac Doplicher Dyson Englert Faddeev Fadin Fayet Fermi Feynman Fierz Fock Frampton Fritzsch Fröhlich Fredenhagen Furry Glashow Gelfand Gell-Mann Glimm Goldstone Gribov Gross Gupta Guralnik Haag Heisenberg Hepp Higgs Hagen 't Hooft Iliopoulos Ivanenko Jackiw Jaffe Jona-Lasinio Jordan Jost Källén Kendall Kinoshita Klebanov Kontsevich Kuraev Landau Lee Lehmann Leutwyler Lipatov Łopuszański Low Lüders Maiani Majorana Maldacena Migdal Mills Møller Naimark Nambu Neveu Nishijima Oehme Oppenheimer Osterwalder Parisi Pauli Peskin Plefka Polyakov Pomeranchuk Popov Proca Rubakov Ruelle Salam Schrader Schwarz Schwinger Segal Seiberg Semenoff Shifman Shirkov Skyrme Sommerfield Stora Stueckelberg Sudarshan Symanzik Thirring Tomonaga Tyutin Vainshtein Veltman Virasoro Ward Weinberg Weisskopf Wentzel Wess Wetterich Weyl Wick Wightman Wigner Wilczek Wilson Witten Yang Yukawa Zamolodchikov Zamolodchikov Zee Zimmermann Zinn-Justin Zuber Zumino
v t e

Renormalization is a collection of techniques in quantum field theory, statistical field theory, and the theory of self-similar geometric structures, that are used to treat infinities arising in calculated quantities by altering values of these quantities to compensate for effects of their self-interactions. But even if no infinities arose in loop diagrams in quantum field theory, it could be shown that it would be necessary to renormalize the mass and fields appearing in the original Lagrangian.^[1]

For example, an electron theory may begin by postulating an electron with an initial mass and charge. In quantum field theory a cloud of virtual particles, such as photons, positrons, and others surrounds and interacts with the initial electron. Accounting for the interactions of the surrounding particles (e.g. collisions at different energies) shows that the electron-system behaves as if it had a different mass and charge than initially postulated. Renormalization, in this example, mathematically replaces the initially postulated mass and charge of an electron with the experimentally observed mass and charge. Mathematics and experiments prove that positrons and more massive particles like protons exhibit precisely the same observed charge as the electron – even in the presence of much stronger interactions and more intense clouds of virtual particles.

Renormalization specifies relationships between parameters in the theory when parameters describing large distance scales differ from parameters describing small distance scales. Physically, the pileup of contributions from an infinity of scales involved in a problem may then result in further infinities. When describing spacetime as a continuum, certain statistical and quantum mechanical constructions are not well-defined. To define them, or make them unambiguous, a continuum limit must carefully remove "construction scaffolding" of lattices at various scales. Renormalization procedures are based on the requirement that certain physical quantities (such as the mass and charge of an electron) equal observed (experimental) values. That is, the experimental value of the physical quantity yields practical applications, but due to their empirical nature the observed measurement represents areas of quantum field theory that require deeper derivation from theoretical bases.

Renormalization was first developed in quantum electrodynamics (QED) to make sense of infinite integrals in perturbation theory. Initially viewed as a suspect provisional procedure even by some of its originators, renormalization eventually was embraced as an important and self-consistent actual mechanism of scale physics in several fields of physics and mathematics. Despite his later skepticism, it was Paul Dirac who pioneered renormalization.^[2][3]

Today, the point of view has shifted: on the basis of the breakthrough renormalization group insights of Nikolay Bogolyubov and Kenneth Wilson, the focus is on variation of physical quantities across contiguous scales, while distant scales are related to each other through "effective" descriptions. All scales are linked in a broadly systematic way, and the actual physics pertinent to each is extracted with the suitable specific computational techniques appropriate for each. Wilson clarified which variables of a system are crucial and which are redundant.

Renormalization is distinct from regularization, another technique to control infinities by assuming the existence of new unknown physics at new scales.

Self-interactions in classical physics

The problem of infinities first arose in the classical electrodynamics of point particles in the 19th and early 20th century.

The mass of a charged particle should include the mass–energy in its electrostatic field (electromagnetic mass). Assume that the particle is a charged spherical shell of radius r_e. The mass–energy in the field is

${\displaystyle m_{\text{em}}=\int {\frac {1}{2}}E^{2}\,dV=\int _{r_{\text{e}}}^{\infty }{\frac {1}{2}}\left({\frac {q}{4\pi r^{2}}}\right)^{2}4\pi r^{2}\,dr={\frac {q^{2}}{8\pi r_{\text{e}}}},}$

which becomes infinite as r_e → 0. This implies that the point particle would have infinite inertia and thus cannot be accelerated. Incidentally, the value of r_e that makes ${\displaystyle m_{\text{em}}}$ equal to the electron mass is called the classical electron radius, which (setting ${\displaystyle q=e}$ and restoring factors of c and ${\displaystyle \varepsilon _{0}}$) turns out to be

${\displaystyle r_{\text{e}}={\frac {e^{2}}{4\pi \varepsilon _{0}m_{\text{e}}c^{2}}}=\alpha {\frac {\hbar }{m_{\text{e}}c}}\approx 2.8\times 10^{-15}~{\text{m}},}$

where ${\displaystyle \alpha \approx 1/137}$ is the fine-structure constant, and ${\displaystyle \hbar /(m_{\text{e}}c)}$ is the reduced Compton wavelength of the electron.

Renormalization: The total effective mass of a spherical charged particle includes the actual bare mass of the spherical shell (in addition to the mass mentioned above associated with its electric field). If the shell's bare mass is allowed to be negative, it might be possible to take a consistent point limit.^{[citation needed]} This was called renormalization, and Lorentz and Abraham attempted to develop a classical theory of the electron this way. This early work was the inspiration for later attempts at regularization and renormalization in quantum field theory.

(See also regularization (physics) for an alternative way to remove infinities from this classical problem, assuming new physics exists at small scales.)

When calculating the electromagnetic interactions of charged particles, it is tempting to ignore the back-reaction of a particle's own field on itself. (Analogous to the back-EMF of circuit analysis.) But this back-reaction is necessary to explain the friction on charged particles when they emit radiation. If the electron is assumed to be a point, the value of the back-reaction diverges, for the same reason that the mass diverges, because the field is inverse-square.

The Abraham–Lorentz theory had a noncausal "pre-acceleration". Sometimes an electron would start moving before the force is applied. This is a sign that the point limit is inconsistent.

The trouble was worse in classical field theory than in quantum field theory, because in quantum field theory a charged particle experiences Zitterbewegung due to interference with virtual particle–antiparticle pairs, thus effectively smearing out the charge over a region comparable to the Compton wavelength. In quantum electrodynamics at small coupling, the electromagnetic mass only diverges as the logarithm of the radius of the particle.

Divergences in quantum electrodynamics

When developing quantum electrodynamics in the 1930s, Max Born, Werner Heisenberg, Pascual Jordan, and Paul Dirac discovered that in perturbative corrections many integrals were divergent (see The problem of infinities).

One way of describing the perturbation theory corrections' divergences was discovered in 1947–49 by Hans Kramers,^[4] Hans Bethe,^[5] Julian Schwinger,^[6][7][8][9] Richard Feynman,^[10][11][12] and Shin'ichiro Tomonaga,^{[13][14][15][16][17][18][19]} and systematized by Freeman Dyson in 1949.^[20] The divergences appear in radiative corrections involving Feynman diagrams with closed loops of virtual particles in them.

While virtual particles obey conservation of energy and momentum, they can have any energy and momentum, even one that is not allowed by the relativistic energy–momentum relation for the observed mass of that particle (that is, ${\displaystyle E^{2}-p^{2}}$ is not necessarily the squared mass of the particle in that process, e.g. for a photon it could be nonzero). Such a particle is called off-shell. When there is a loop, the momentum of the particles involved in the loop is not uniquely determined by the energies and momenta of incoming and outgoing particles. A variation in the energy of one particle in the loop can be balanced by an equal and opposite change in the energy of another particle in the loop, without affecting the incoming and outgoing particles. Thus many variations are possible. So to find the amplitude for the loop process, one must integrate over all possible combinations of energy and momentum that could travel around the loop.

These integrals are often divergent, that is, they give infinite answers. The divergences that are significant are the "ultraviolet" (UV) ones. An ultraviolet divergence can be described as one that comes from

• the region in the integral where all particles in the loop have large energies and momenta,
• very short wavelengths and high-frequencies fluctuations of the fields, in the path integral for the field,
• very short proper-time between particle emission and absorption, if the loop is thought of as a sum over particle paths.

So these divergences are short-distance, short-time phenomena.

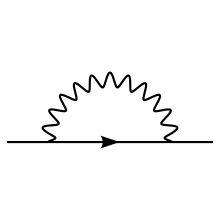
Shown in the pictures at the right margin, there are exactly three one-loop divergent loop diagrams in quantum electrodynamics:^[21]

(a) A photon creates a virtual electron–positron pair, which then annihilates. This is a vacuum polarization diagram.

(b) An electron quickly emits and reabsorbs a virtual photon, called a self-energy.

(c) An electron emits a photon, emits a second photon, and reabsorbs the first. This process is shown in the section below in figure 2, and it is called a vertex renormalization. The Feynman diagram for this is also called a “penguin diagram” due to its shape remotely resembling a penguin.

The three divergences correspond to the three parameters in the theory under consideration:

1. The field normalization Z.
2. The mass of the electron.
3. The charge of the electron.

The second class of divergence called an infrared divergence, is due to massless particles, like the photon. Every process involving charged particles emits infinitely many coherent photons of infinite wavelength, and the amplitude for emitting any finite number of photons is zero. For photons, these divergences are well understood. For example, at the 1-loop order, the vertex function has both ultraviolet and infrared divergences. In contrast to the ultraviolet divergence, the infrared divergence does not require the renormalization of a parameter in the theory involved. The infrared divergence of the vertex diagram is removed by including a diagram similar to the vertex diagram with the following important difference: the photon connecting the two legs of the electron is cut and replaced by two on-shell (i.e. real) photons whose wavelengths tend to infinity; this diagram is equivalent to the bremsstrahlung process. This additional diagram must be included because there is no physical way to distinguish a zero-energy photon flowing through a loop as in the vertex diagram and zero-energy photons emitted through bremsstrahlung. From a mathematical point of view, the IR divergences can be regularized by assuming fractional differentiation w.r.t. a parameter, for example:

${\displaystyle {\left(p^2-<!--\; -\; -->a^2\right)}^{\frac{1}{2}}}$Zdroj:https://en.wikipedia.org?pojem=Renormalizable
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---