A | B | C | D | E | F | G | H | CH | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
| Regular hexahedron | |
|---|---|
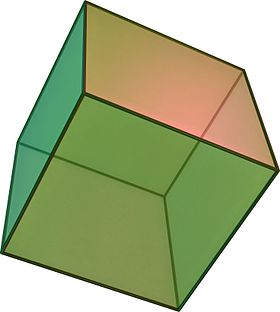 (Click here for rotating model) | |
| Type | Platonic solid |
| Elements | F = 6, E = 12 V = 8 (χ = 2) |
| Faces by sides | 6{4} |
| Conway notation | C |
| Schläfli symbols | {4,3} |
| t{2,4} or {4}×{} tr{2,2} {}×{}×{} = {}3 | |
| Face configuration | V3.3.3.3 |
| Wythoff symbol | 3 | 2 4 |
| Coxeter diagram | |
| Symmetry | Oh, B3, , (*432) |
| Rotation group | O, +, (432) |
| References | U06, C18, W3 |
| Properties | regular, convexzonohedron, Hanner polytope |
| Dihedral angle | 90° |
 4.4.4 (Vertex figure) |
 Octahedron (dual polyhedron) |
 Net | |

In geometry, a cube[a] is a three-dimensional solid object bounded by six square faces, facets, or sides, with three meeting at each vertex. Viewed from a corner, it is a hexagon and its net is usually depicted as a cross.[1]
The cube is the only regular hexahedron and is one of the five Platonic solids. It has 6 faces, 12 edges, and 8 vertices.
The cube is also a square parallelepiped, an equilateral cuboid, a right rhombohedron, and a 3-zonohedron. It is a regular square prism in three orientations, and a trigonal trapezohedron in four orientations.
The cube is dual to the octahedron. It has cubical or octahedral symmetry, and is the only convex polyhedron whose faces are all squares. Its generalization for higher-dimensional spaces is called a hypercube.
Orthogonal projections
The cube has four special orthogonal projections, centered, on a vertex, edges, face and normal to its vertex figure. The first and third correspond to the A2 and B2 Coxeter planes.
| Centered by | Face | Vertex |
|---|---|---|
| Coxeter planes | B2
|
A2
|
| Projective symmetry |
||
| Tilted views | 
|

|
Spherical tiling
The cube can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.

|

|
| Orthographic projection | Stereographic projection |
|---|
Cartesian coordinates
For a cube centered at the origin, with edges parallel to the axes and with an edge length of 2, the Cartesian coordinates of the vertices are
- (±1, ±1, ±1)
while the interior consists of all points (x0, x1, x2) with −1 < xi < 1 for all i.
As a configuration
This configuration matrix represents the cube. The rows and columns correspond to vertices, edges, and faces. The diagonal numbers say how many of each element occur in the whole cube. The nondiagonal numbers say how many of the column's element occur in or at the row's element.[2] For example, the 2 in the first column of the middle row indicates that there are 2 vertices in (i.e., at the extremes of) each edge; the 3 in the middle column of the first row indicates that 3 edges meet at each vertex.
Equation in three dimensional space
In analytic geometry, a cube's surface with center (x0, y0, z0) and edge length of 2a is the locus of all points (x, y, z) such that
A cube can also be considered the limiting case of a 3D superellipsoid as all three exponents approach infinity.
Formulas
For a cube of edge length :
| surface area | volume | ||
| face diagonal | space diagonal | ||
| radius of circumscribed sphere | radius of sphere tangent to edges | ||
| radius of inscribed sphere | angles between faces (in radians) |
As the volume of a cube is the third power of its sides , third powers are called cubes, by analogy with squares and second powers.
A cube has the largest volume among cuboids (rectangular boxes) with a given surface area. Also, a cube has the largest volume among cuboids with the same total linear size (length+width+height).
Point in space
For a cube whose circumscribing sphere has radius R, and for a given point in its 3-dimensional space with distances di from the cube's eight vertices, we have:[3]
Doubling the cube
Doubling the cube, or the Delian problem, was the problem posed by ancient Greek mathematicians of using only a compass and straightedge to start with the length of the edge of a given cube and to construct the length of the edge of a cube with twice the volume of the original cube. They were unable to solve this problem, which in 1837 Pierre Wantzel proved it to be impossible because the cube root of 2 is not a constructible number.
Uniform colorings and symmetry

The cube has three uniform colorings, named by the unique colors of the square faces around each vertex: 111, 112, 123.
The cube has four classes of symmetry, which can be represented by vertex-transitive coloring the faces. The highest octahedral symmetry Oh has all the faces the same color. The dihedral symmetry D4h comes from the cube being a solid, with all the six sides being different colors. The prismatic subsets D2d has the same coloring as the previous one and D2h has alternating colors for its sides for a total of three colors, paired by opposite sides. Each symmetry form has a different Wythoff symbol.