In physical chemistry, the Arrhenius equation is a formula for the temperature dependence of reaction rates. The equation was proposed by Svante Arrhenius in 1889, based on the work of Dutch chemist Jacobus Henricus van 't Hoff who had noted in 1884 that the van 't Hoff equation for the temperature dependence of equilibrium constants suggests such a formula for the rates of both forward and reverse reactions. This equation has a vast and important application in determining the rate of chemical reactions and for calculation of energy of activation. Arrhenius provided a physical justification and interpretation for the formula.^[1][2][3][4] Currently, it is best seen as an empirical relationship.^[5]: 188 It can be used to model the temperature variation of diffusion coefficients, population of crystal vacancies, creep rates, and many other thermally induced processes and reactions. The Eyring equation, developed in 1935, also expresses the relationship between rate and energy.

Equation

The Arrhenius equation gives the dependence of the rate constant of a chemical reaction on the absolute temperature as

$${\displaystyle k=Ae^{\frac {-E_{\text{a}}}{RT}},}$$

• k is the rate constant (frequency of collisions resulting in a reaction),
• T is the absolute temperature,
• A is the pre-exponential factor or Arrhenius factor or frequency factor. Arrhenius originally considered A to be a temperature-independent constant for each chemical reaction.^[6] However more recent treatments include some temperature dependence – see § Modified Arrhenius equation below.
• E_a is the molar activation energy for the reaction,
• R is the universal gas constant.^[1][2][4]

Alternatively, the equation may be expressed as

$${\displaystyle k=Ae^{\frac {-E_{\text{a}}}{k_{\text{B}}T}},}$$

• E_a is the activation energy for the reaction (in the same unit as k_BT),
• k_B is the Boltzmann constant.

The only difference is the unit of E_a: the former form uses energy per mole, which is common in chemistry, while the latter form uses energy per molecule directly, which is common in physics. The different units are accounted for in using either the gas constant, R, or the Boltzmann constant, k_B, as the multiplier of temperature T.

The unit of the pre-exponential factor A are identical to those of the rate constant and will vary depending on the order of the reaction. If the reaction is first order it has the unit s⁻¹, and for that reason it is often called the frequency factor or attempt frequency of the reaction. Most simply, k is the number of collisions that result in a reaction per second, A is the number of collisions (leading to a reaction or not) per second occurring with the proper orientation to react^[7] and ${\displaystyle e^{\frac {-E_{\text{a}}}{RT}}}$ is the probability that any given collision will result in a reaction. It can be seen that either increasing the temperature or decreasing the activation energy (for example through the use of catalysts) will result in an increase in rate of reaction.

Given the small temperature range of kinetic studies, it is reasonable to approximate the activation energy as being independent of the temperature. Similarly, under a wide range of practical conditions, the weak temperature dependence of the pre-exponential factor is negligible compared to the temperature dependence of the factor ${\displaystyle e^{\frac {-E_{\text{a}}}{RT}}}$; except in the case of "barrierless" diffusion-limited reactions, in which case the pre-exponential factor is dominant and is directly observable.

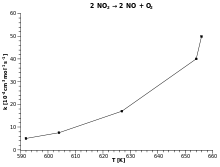
With this equation it can be roughly estimated that the rate of reaction increases by a factor of about 2 to 3 for every 10 °C rise in temperature, for common values of activation energy and temperature range.^[8]

The ${\displaystyle e^{\frac {-E_{a}}{RT}}}$ factor denotes the fraction of molecules with energy greater than or equal to ${\displaystyle E_{a}}$.^[9]

Derivation

Van't Hoff argued that the temperature ${\displaystyle T}$ of a reaction and the standard equilibrium constant ${\displaystyle k_{\text{e}}^{0}}$ exhibit the relation:

$${\displaystyle {\frac {d\ln k_{\text{e}}^{0}}{dT}}={\frac {\Delta U^{0}}{RT^{2}}}}$$

(1)

where ${\displaystyle \Delta U^{0}}$ denotes the apposite standard internal energy change value.

Let ${\displaystyle k_{\text{f}}}$ and ${\displaystyle k_{\text{b}}}$ respectively denote the forward and backward reaction rates of the reaction of interest, then ${\displaystyle k_{\text{e}}^{0}={\frac {k_{\text{f}}}{k_{\text{b}}}}}$,^[10] an equation from which ${\displaystyle \ln k_{\text{e}}^{0}=\ln k_{\text{f}}-\ln k_{\text{b}}}$ naturally follows.

Substituting the expression for ${\displaystyle \ln k_{\text{e}}^{0}}$ in eq.(1), we obtain ${\displaystyle {\frac {d\ln k_{\text{f}}}{dT}}-{\frac {d\ln k_{\text{b}}}{dT}}={\frac {\Delta U^{0}}{RT^{2}}}}$.

The preceding equation can be broken down into the following two equations:

${\displaystyle {\frac {d\ln k_{\text{f}}}{dT}}={\text{constant}}+{\frac {E_{\text{f}}}{RT^{2}}}}$

(2)

and

${\displaystyle {\frac {d\ln k_{\text{b}}}{dT}}={\text{constant}}+{\frac {E_{\text{b}}}{RT^{2}}}}$

(3)

where ${\displaystyle E_{\text{f}}}$ and ${\displaystyle E_{\text{b}}}$ are the activation energies associated with the forward and backward reactions respectively, with ${\displaystyle \Delta U^{0}=E_{\text{f}}-E_{\text{b}}}$.

Experimental findings suggest that the constants in eq.(2) and eq.(3) can be treated as being equal to zero, so that