Flux describes any effect that appears to pass or travel (whether it actually moves or not) through a surface or substance. Flux is a concept in applied mathematics and vector calculus which has many applications to physics. For transport phenomena, flux is a vector quantity, describing the magnitude and direction of the flow of a substance or property. In vector calculus flux is a scalar quantity, defined as the surface integral of the perpendicular component of a vector field over a surface.^[1]

Terminology

The word flux comes from Latin: fluxus means "flow", and fluere is "to flow".^[2] As fluxion, this term was introduced into differential calculus by Isaac Newton.

The concept of heat flux was a key contribution of Joseph Fourier, in the analysis of heat transfer phenomena.^[3] His seminal treatise Théorie analytique de la chaleur (The Analytical Theory of Heat),^[4] defines fluxion as a central quantity and proceeds to derive the now well-known expressions of flux in terms of temperature differences across a slab, and then more generally in terms of temperature gradients or differentials of temperature, across other geometries. One could argue, based on the work of James Clerk Maxwell,^[5] that the transport definition precedes the definition of flux used in electromagnetism. The specific quote from Maxwell is:

In the case of fluxes, we have to take the integral, over a surface, of the flux through every element of the surface. The result of this operation is called the surface integral of the flux. It represents the quantity which passes through the surface.

— James Clerk Maxwell

According to the transport definition, flux may be a single vector, or it may be a vector field / function of position. In the latter case flux can readily be integrated over a surface. By contrast, according to the electromagnetism definition, flux is the integral over a surface; it makes no sense to integrate a second-definition flux for one would be integrating over a surface twice. Thus, Maxwell's quote only makes sense if "flux" is being used according to the transport definition (and furthermore is a vector field rather than single vector). This is ironic because Maxwell was one of the major developers of what we now call "electric flux" and "magnetic flux" according to the electromagnetism definition. Their names in accordance with the quote (and transport definition) would be "surface integral of electric flux" and "surface integral of magnetic flux", in which case "electric flux" would instead be defined as "electric field" and "magnetic flux" defined as "magnetic field". This implies that Maxwell conceived of these fields as flows/fluxes of some sort.

Given a flux according to the electromagnetism definition, the corresponding flux density, if that term is used, refers to its derivative along the surface that was integrated. By the Fundamental theorem of calculus, the corresponding flux density is a flux according to the transport definition. Given a current such as electric current—charge per time, current density would also be a flux according to the transport definition—charge per time per area. Due to the conflicting definitions of flux, and the interchangeability of flux, flow, and current in nontechnical English, all of the terms used in this paragraph are sometimes used interchangeably and ambiguously. Concrete fluxes in the rest of this article will be used in accordance to their broad acceptance in the literature, regardless of which definition of flux the term corresponds to.

Flux as flow rate per unit area

In transport phenomena (heat transfer, mass transfer and fluid dynamics), flux is defined as the rate of flow of a property per unit area, which has the dimensions ·⁻¹·⁻¹.^[6] The area is of the surface the property is flowing "through" or "across". For example, the amount of water that flows through a cross section of a river each second divided by the area of that cross section, or the amount of sunlight energy that lands on a patch of ground each second divided by the area of the patch, are kinds of flux.

General mathematical definition (transport)

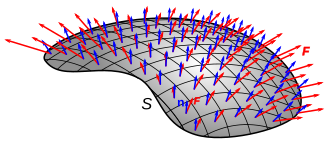
Here are 3 definitions in increasing order of complexity. Each is a special case of the following. In all cases the frequent symbol j, (or J) is used for flux, q for the physical quantity that flows, t for time, and A for area. These identifiers will be written in bold when and only when they are vectors.

First, flux as a (single) scalar:

where In this case the surface in which flux is being measured is fixed and has area A. The surface is assumed to be flat, and the flow is assumed to be everywhere constant with respect to position and perpendicular to the surface.

Second, flux as a scalar field defined along a surface, i.e. a function of points on the surface:

As before, the surface is assumed to be flat, and the flow is assumed to be everywhere perpendicular to it. However the flow need not be constant. q is now a function of p, a point on the surface, and A, an area. Rather than measure the total flow through the surface, q measures the flow through the disk with area A centered at p along the surface.

Finally, flux as a vector field:

In this case, there is no fixed surface we are measuring over. q is a function of a point, an area, and a direction (given by a unit vector ${\displaystyle \mathbf {\hat {n}} }$), and measures the flow through the disk of area A perpendicular to that unit vector. I is defined picking the unit vector that maximizes the flow around the point, because the true flow is maximized across the disk that is perpendicular to it. The unit vector thus uniquely maximizes the function when it points in the "true direction" of the flow. (Strictly speaking, this is an abuse of notation because the "arg max" cannot directly compare vectors; we take the vector with the biggest norm instead.)

Properties

These direct definitions, especially the last, are rather unwieldy. For example, the arg max construction is artificial from the perspective of empirical measurements, when with a weathervane or similar one can easily deduce the direction of flux at a point. Rather than defining the vector flux directly, it is often more intuitive to state some properties about it. Furthermore, from these properties the flux can uniquely be determined anyway.

If the flux j passes through the area at an angle θ to the area normal ${\displaystyle \mathbf {\hat {n}} }$, then the dot product

That is, the component of flux passing through the surface (i.e. normal to it) is j cos θ, while the component of flux passing tangential to the area is j sin θ, but there is no flux actually passing through the area in the tangential direction. The only component of flux passing normal to the area is the cosine component.

For vector flux, the surface integral of j over a surface S, gives the proper flowing per unit of time through the surface:

where A (and its infinitesimal) is the vector area – combination ${\displaystyle \mathbf {A} =A\mathbf {\hat {n}} }$ of the magnitude of the area A through which the property passes and a unit vector ${\displaystyle \mathbf {\hat {n}} }$ normal to the area. Unlike in the second set of equations, the surface here need not be flat.

Finally, we can integrate again over the time duration t₁ to t₂, getting the total amount of the property flowing through the surface in that time (t₂ − t₁):

Transport fluxes

Eight of the most common forms of flux from the transport phenomena literature are defined as follows:

1. Momentum flux, the rate of transfer of momentum across a unit area (N·s·m⁻²·s⁻¹). (Newton's law of viscosity)^[7]
2. Heat flux, the rate of heat flow across a unit area (J·m⁻²·s⁻¹). (Fourier's law of conduction)^[8] (This definition of heat flux fits Maxwell's original definition.)^[5]
3. Diffusion flux, the rate of movement of molecules across a unit area (mol·m⁻²·s⁻¹). (Fick's law of diffusion)^[7]
4. Volumetric flux, the rate of volume flow across a unit area (m³·m⁻²·s⁻¹). (Darcy's law of groundwater flow)
5. Mass flux, the rate of mass flow across a unit area (kg·m⁻²·s⁻¹). (Either an alternate form of Fick's law that includes the molecular mass, or an alternate form of Darcy's law that includes the density.)
6. Radiative flux, the amount of energy transferred in the form of photons at a certain distance from the source per unit area per second (J·m⁻²·s⁻¹). Used in astronomy to determine the magnitude and spectral class of a star. Also acts as a generalization of heat flux, which is equal to the radiative flux when restricted to the electromagnetic spectrum.
7. Energy flux, the rate of transfer of energy through a unit area (J·m⁻²·s⁻¹). The radiative flux and heat flux are specific cases of energy flux.
8. Particle flux, the rate of transfer of particles through a unit area ( m⁻²·s⁻¹)

These fluxes are vectors at each point in space, and have a definite magnitude and direction. Also, one can take the divergence of any of these fluxes to determine the accumulation rate of the quantity in a control volume around a given point in space. For incompressible flow, the divergence of the volume flux is zero.

Chemical diffusion

As mentioned above, chemical molar flux of a component A in an isothermal, isobaric system is defined in Fick's law of diffusion as:

where the nabla symbol ∇ denotes the gradient operator, D_AB is the diffusion coefficient (m²·s⁻¹) of component A diffusing through component B, c_A is the concentration (mol/m³) of component A.^[9]

This flux has units of mol·m⁻²·s⁻¹, and fits Maxwell's original definition of flux.^[5]

For dilute gases, kinetic molecular theory relates the diffusion coefficient D to the particle density n = N/V, the molecular mass m, the collision cross section ${\displaystyle \sigma }$, and the absolute temperature T by

where the second factor is the mean free path and the square root (with the Boltzmann constant k) is the mean velocity of the particles.

In turbulent flows, the transport by eddy motion can be expressed as a grossly increased diffusion coefficient.

Quantum mechanics

In quantum mechanics, particles of mass m in the quantum state ψ(r, t) have a probability density defined as

So the probability of finding a particle in a differential volume element d³r is Then the number of particles passing perpendicularly through unit area of a cross-section per unit time is the probability flux;