The Collatz conjecture^[a] is one of the most famous unsolved problems in mathematics. The conjecture asks whether repeating two simple arithmetic operations will eventually transform every positive integer into 1. It concerns sequences of integers in which each term is obtained from the previous term as follows: if the previous term is even, the next term is one half of the previous term. If the previous term is odd, the next term is 3 times the previous term plus 1. The conjecture is that these sequences always reach 1, no matter which positive integer is chosen to start the sequence. The conjecture has been shown to hold for all positive integers up to 2.95×10²⁰, but no general proof has been found.

It is named after the mathematician Lothar Collatz, who introduced the idea in 1937, two years after receiving his doctorate.^[4] The sequence of numbers involved is sometimes referred to as the hailstone sequence, hailstone numbers or hailstone numerals (because the values are usually subject to multiple descents and ascents like hailstones in a cloud),^[5] or as wondrous numbers.^[6]

Paul Erdős said about the Collatz conjecture: "Mathematics may not be ready for such problems."^[7] Jeffrey Lagarias stated in 2010 that the Collatz conjecture "is an extraordinarily difficult problem, completely out of reach of present day mathematics".^[8]

Statement of the problem

Consider the following operation on an arbitrary positive integer:

• If the number is even, divide it by two.
• If the number is odd, triple it and add one.

In modular arithmetic notation, define the function f as follows:

Now form a sequence by performing this operation repeatedly, beginning with any positive integer, and taking the result at each step as the input at the next.

In notation:

(that is: a_i is the value of f applied to n recursively i times; a_i = f ⁱ(n)).

The Collatz conjecture is: This process will eventually reach the number 1, regardless of which positive integer is chosen initially. That is, for each ${\displaystyle n}$, there is some ${\displaystyle i}$ with ${\displaystyle a_{i}=1}$.

If the conjecture is false, it can only be because there is some starting number which gives rise to a sequence that does not contain 1. Such a sequence would either enter a repeating cycle that excludes 1, or increase without bound. No such sequence has been found.

The smallest i such that a_i < a₀ is called the stopping time of n. Similarly, the smallest k such that a_k = 1 is called the total stopping time of n.^[2] If one of the indexes i or k doesn't exist, we say that the stopping time or the total stopping time, respectively, is infinite.

The Collatz conjecture asserts that the total stopping time of every n is finite. It is also equivalent to saying that every n ≥ 2 has a finite stopping time.

Since 3n + 1 is even whenever n is odd, one may instead use the "shortcut" form of the Collatz function:

This definition yields smaller values for the stopping time and total stopping time without changing the overall dynamics of the process.

Empirical data

For instance, starting with n = 12 and applying the function f without "shortcut", one gets the sequence 12, 6, 3, 10, 5, 16, 8, 4, 2, 1.

The number n = 19 takes longer to reach 1: 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1.

The sequence for n = 27, listed and graphed below, takes 111 steps (41 steps through odd numbers, in bold), climbing as high as 9232 before descending to 1.

27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1 (sequence A008884 in the OEIS)

Numbers with a total stopping time longer than that of any smaller starting value form a sequence beginning with:

1, 2, 3, 6, 7, 9, 18, 25, 27, 54, 73, 97, 129, 171, 231, 313, 327, 649, 703, 871, 1161, 2223, 2463, 2919, 3711, 6171, ... (sequence A006877 in the OEIS).

The starting values whose maximum trajectory point is greater than that of any smaller starting value are as follows:

1, 2, 3, 7, 15, 27, 255, 447, 639, 703, 1819, 4255, 4591, 9663, 20895, 26623, 31911, 60975, 77671, 113383, 138367, 159487, 270271, 665215, 704511, ... (sequence A006884 in the OEIS)

Number of steps for n to reach 1 are

0, 1, 7, 2, 5, 8, 16, 3, 19, 6, 14, 9, 9, 17, 17, 4, 12, 20, 20, 7, 7, 15, 15, 10, 23, 10, 111, 18, 18, 18, 106, 5, 26, 13, 13, 21, 21, 21, 34, 8, 109, 8, 29, 16, 16, 16, 104, 11, 24, 24, ... (sequence A006577 in the OEIS)

The starting value having the largest total stopping time while being

less than 10 is 9, which has 19 steps,

less than 100 is 97, which has 118 steps,

less than 1000 is 871, which has 178 steps,

less than 10⁴ is 6171, which has 261 steps,

less than 10⁵ is 77031, which has 350 steps,

less than 10⁶ is 837799, which has 524 steps,

less than 10⁷ is 8400511, which has 685 steps,

less than 10⁸ is 63728127, which has 949 steps,

less than 10⁹ is 670617279, which has 986 steps,

less than 10¹⁰ is 9780657630, which has 1132 steps,^[9]

less than 10¹¹ is 75128138247, which has 1228 steps,

less than 10¹² is 989345275647, which has 1348 steps.^[10] (sequence A284668 in the OEIS)

These numbers are the lowest ones with the indicated step count, but not necessarily the only ones below the given limit. As an example, 9780657631 has 1132 steps, as does 9780657630.

The starting values having the smallest total stopping time with respect to their number of digits (in base 2) are the powers of two since 2ⁿ is halved n times to reach 1, and is never increased.

Visualizations

• 
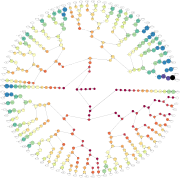
  Directed graph showing the orbits of the first 1000 numbers.
• 
  The x axis represents starting number, the y axis represents the highest number reached during the chain to 1. This plot shows a restricted y axis: some x values produce intermediates as high as 2.7×10⁷ (for x = 9663)
• 
  The same plot as the previous one but on log scale, so all y values are shown. The first thick line towards the middle of the plot corresponds to the tip at 27, which reaches a maximum at 9232.
• 
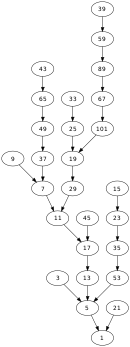
  The tree of all the numbers having fewer than 20 steps.
• 
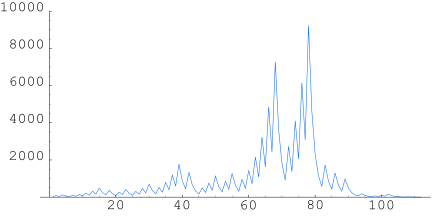
  The number of iterations it takes to get to one for the first 100 million numbers.

Supporting arguments

Although the conjecture has not been proven, most mathematicians who have looked into the problem think the conjecture is true because experimental evidence and heuristic arguments support it.

Experimental evidence

As of 2020^[update], the conjecture has been checked by computer for all starting values up to 2⁶⁸ ≈ 2.95×10²⁰. All values tested so far converge to 1.^[11]

This computer evidence is still not rigorous proof that the conjecture is true for all starting values, as counterexamples may be found when considering very large (or possibly immense) positive integers, as in the case of the disproven Pólya conjecture and Mertens conjecture.

However, such verifications may have other implications. For example, one can derive additional constraints on the period and structural form of a non-trivial cycle.^{[12][13][14][clarification needed]}

A probabilistic heuristic

If one considers only the odd numbers in the sequence generated by the Collatz process, then each odd number is on average 3/4 of the previous one.^[15] (More precisely, the geometric mean of the ratios of outcomes is 3/4.) This yields a heuristic argument that every Hailstone sequence should decrease in the long run, although this is not evidence against other cycles, only against divergence. The argument is not a proof because it assumes that Hailstone sequences are assembled from uncorrelated probabilistic events. (It does rigorously establish that the 2-adic extension of the Collatz process has two division steps for every multiplication step for almost all 2-adic starting values.)

Stopping times

As proven by Riho Terras, almost every positive integer has a finite stopping time.^[16] In other words, almost every Collatz sequence reaches a point that is strictly below its initial value. The proof is based on the distribution of parity vectors and uses the central limit theorem.

In 2019, Terence Tao improved this result by showing, using logarithmic density, that almost all (in the sense of logarithmic density) Collatz orbits are descending below any given function of the starting point, provided that this function diverges to infinity, no matter how slowly. Responding to this work, Quanta Magazine wrote that Tao "came away with one of the most significant results on the Collatz conjecture in decades".^[17][18]

Lower bounds

In a computer-aided proof, Krasikov and Lagarias showed that the number of integers in the interval that eventually reach 1 is at least equal to x^0.84 for all sufficiently large x.^[19]

Cycles

In this part, consider the shortcut form of the Collatz function

A cycle is a sequence (a₀, a₁, ..., a_q) of distinct positive integers where f(a₀) = a₁, f(a₁) = a₂, ..., and f(a_q) = a₀.

The only known cycle is (1,2) of period 2, called the trivial cycle.

Cycle length

The length of a non-trivial cycle is known to be at least 114208327604 (or 186265759595 without short-cut). If it can be shown that for all positive integers less than ${\displaystyle 3\times 2^{69}}$ the Collatz sequences reach 1, then this bound would raise to 217976794617 (355504839929 without short-cut).^[20][13] In fact, Eliahou (1993) proved that the period p of any non-trivial cycle is of the form

where a, b and c are non-negative integers, b ≥ 1 and ac = 0. This result is based on the continued fraction expansion of ln 3/ln 2.^[13]

k-cycles

A k-cycle is a cycle that can be partitioned into k contiguous subsequences, each consisting of an increasing sequence of odd numbers, followed by a decreasing sequence of even numbers.^[14] For instance, if the cycle consists of a single increasing sequence of odd numbers followed by a decreasing sequence of even numbers, it is called a 1-cycle.

Steiner (1977) proved that there is no 1-cycle other than the trivial (1; 2).^[21] Simons (2005) used Steiner's method to prove that there is no 2-cycle.^[22] Simons & de Weger (2005) extended this proof up to 68-cycles; there is no k-cycle up to k = 68.^[14] Hercher extended the method further and proved that there exists no k-cycle with k≤91.^[20] As exhaustive computer searches continue, larger k values may be ruled out. To state the argument more intuitively; we do not have to search for cycles that have less than 92 subsequences, where each subsequence consists of consecutive ups followed by consecutive downs.

Other formulations of the conjecture

In reverse

There is another approach to prove the conjecture, which considers the bottom-up method of growing the so-called Collatz graph. The Collatz graph is a graph defined by the inverse relation