This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (April 2016) (Learn how and when to remove this template message)

In geometry, a three-dimensional space (3D space, 3-space or, rarely, tri-dimensional space) is a mathematical space in which three values (coordinates) are required to determine the position of a point. Most commonly, it is the three-dimensional Euclidean space, that is, the Euclidean space of dimension three, which models physical space. More general three-dimensional spaces are called 3-manifolds. The term may also refer colloquially to a subset of space, a three-dimensional region (or 3D domain),^[1] a solid figure.

Technically, a tuple of n numbers can be understood as the Cartesian coordinates of a location in a n-dimensional Euclidean space. The set of these n-tuples is commonly denoted ${\displaystyle \mathbb {R} ^{n},}$ and can be identified to the pair formed by a n-dimensional Euclidean space and a Cartesian coordinate system. When n = 3, this space is called the three-dimensional Euclidean space (or simply "Euclidean space" when the context is clear).^[2] In classical physics, it serves as a model of the physical universe, in which all known matter exists. When relativity theory is considered, it can be considered a local subspace of space-time.^[3] While this space remains the most compelling and useful way to model the world as it is experienced,^[4] it is only one example of a large variety of spaces in three dimensions called 3-manifolds. In this classical example, when the three values refer to measurements in different directions (coordinates), any three directions can be chosen, provided that these directions do not lie in the same plane. Furthermore, if these directions are pairwise perpendicular, the three values are often labeled by the terms width/breadth, height/depth, and length.

History

Books XI to XIII of Euclid's Elements dealt with three-dimensional geometry. Book XI develops notions of orthogonality and parallelism of lines and planes, and defines solids including parallelpipeds, pyramids, prisms, spheres, octahedra, icosahedra and dodecahedra. Book XII develops notions of similarity of solids. Book XIII describes the construction of the five regular Platonic solids in a sphere.

In the 17th century, three-dimensional space was described with Cartesian coordinates, with the advent of analytic geometry developed by René Descartes in his work La Géométrie and Pierre de Fermat in the manuscript Ad locos planos et solidos isagoge (Introduction to Plane and Solid Loci), which was unpublished during Fermat's lifetime. However, only Fermat's work dealt with three-dimensional space.

In the 19th century, developments of the geometry of three-dimensional space came with William Rowan Hamilton's development of the quaternions. In fact, it was Hamilton who coined the terms scalar and vector, and they were first defined within his geometric framework for quaternions. Three dimensional space could then be described by quaternions ${\displaystyle q=a+ui+vj+wk}$ which had vanishing scalar component, that is, ${\displaystyle a=0}$. While not explicitly studied by Hamilton, this indirectly introduced notions of basis, here given by the quaternion elements ${\displaystyle i,j,k}$, as well as the dot product and cross product, which correspond to (the negative of) the scalar part and the vector part of the product of two vector quaternions.

It was not until Josiah Willard Gibbs that these two products were identified in their own right, and the modern notation for the dot and cross product were introduced in his classroom teaching notes, found also in the 1901 textbook Vector Analysis written by Edwin Bidwell Wilson based on Gibbs' lectures.

Also during the 19th century came developments in the abstract formalism of vector spaces, with the work of Hermann Grassmann and Giuseppe Peano, the latter of whom first gave the modern definition of vector spaces as an algebraic structure.

In Euclidean geometry

Coordinate systems

Geometry
Projecting a sphere to a plane
Outline History (Timeline)
Branches Euclidean Non-Euclidean Elliptic Spherical Hyperbolic Non-Archimedean geometry Projective Affine Synthetic Analytic Algebraic Arithmetic Diophantine Differential Riemannian Symplectic Discrete differential Complex Finite Discrete/Combinatorial Digital Convex Computational Fractal Incidence Noncommutative geometry Noncommutative algebraic geometry
Concepts Features Dimension Straightedge and compass constructions Angle Curve Diagonal Orthogonality (Perpendicular) Parallel Vertex Congruence Similarity Symmetry
Zero-dimensional Point
One-dimensional Line segment ray Length
Two-dimensional Plane Area Polygon Triangle Altitude Hypotenuse Pythagorean theorem Parallelogram Square Rectangle Rhombus Rhomboid Quadrilateral Trapezoid Kite Circle Diameter Circumference Area
Three-dimensional Volume Cube cuboid Cylinder Dodecahedron Icosahedron Octahedron Pyramid Platonic Solid Sphere Tetrahedron
Four- / other-dimensional Tesseract Hypersphere
Geometers
by name Aida Aryabhata Ahmes Alhazen Apollonius Archimedes Atiyah Baudhayana Bolyai Brahmagupta Cartan Coxeter Descartes Euclid Euler Gauss Gromov Hilbert Huygens Jyeṣṭhadeva Kātyāyana Khayyám Klein Lobachevsky Manava Minkowski Minggatu Pascal Pythagoras Parameshvara Poincaré Riemann Sakabe Sijzi al-Tusi Veblen Virasena Yang Hui al-Yasamin Zhang List of geometers
by period BCE Ahmes Baudhayana Manava Pythagoras Euclid Archimedes Apollonius 1–1400s Zhang Kātyāyana Aryabhata Brahmagupta Virasena Alhazen Sijzi Khayyám al-Yasamin al-Tusi Yang Hui Parameshvara 1400s–1700s Jyeṣṭhadeva Descartes Pascal Huygens Minggatu Euler Sakabe Aida 1700s–1900s Gauss Lobachevsky Bolyai Riemann Klein Poincaré Hilbert Minkowski Cartan Veblen Coxeter Present day Atiyah Gromov
v t e

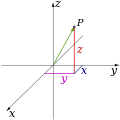
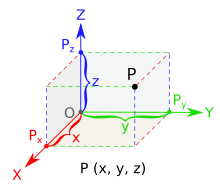
In mathematics, analytic geometry (also called Cartesian geometry) describes every point in three-dimensional space by means of three coordinates. Three coordinate axes are given, each perpendicular to the other two at the origin, the point at which they cross. They are usually labeled x, y, and z. Relative to these axes, the position of any point in three-dimensional space is given by an ordered triple of real numbers, each number giving the distance of that point from the origin measured along the given axis, which is equal to the distance of that point from the plane determined by the other two axes.^[5]

Other popular methods of describing the location of a point in three-dimensional space include cylindrical coordinates and spherical coordinates, though there are an infinite number of possible methods. For more, see Euclidean space.

Below are images of the above-mentioned systems.

• 
  Cartesian coordinate system
• 
  Cylindrical coordinate system
• 
  Spherical coordinate system

Lines and planes

Two distinct points always determine a (straight) line. Three distinct points are either collinear or determine a unique plane. On the other hand, four distinct points can either be collinear, coplanar, or determine the entire space.

Two distinct lines can either intersect, be parallel or be skew. Two parallel lines, or two intersecting lines, lie in a unique plane, so skew lines are lines that do not meet and do not lie in a common plane.

Two distinct planes can either meet in a common line or are parallel (i.e., do not meet). Three distinct planes, no pair of which are parallel, can either meet in a common line, meet in a unique common point, or have no point in common. In the last case, the three lines of intersection of each pair of planes are mutually parallel.

A line can lie in a given plane, intersect that plane in a unique point, or be parallel to the plane. In the last case, there will be lines in the plane that are parallel to the given line.

A hyperplane is a subspace of one dimension less than the dimension of the full space. The hyperplanes of a three-dimensional space are the two-dimensional subspaces, that is, the planes. In terms of Cartesian coordinates, the points of a hyperplane satisfy a single linear equation, so planes in this 3-space are described by linear equations. A line can be described by a pair of independent linear equations—each representing a plane having this line as a common intersection.

Varignon's theorem states that the midpoints of any quadrilateral in ${\displaystyle \mathbb {R} ^{3}}$ form a parallelogram, and hence are coplanar.

Spheres and balls

A sphere in 3-space (also called a 2-sphere because it is a 2-dimensional object) consists of the set of all points in 3-space at a fixed distance r from a central point P. The solid enclosed by the sphere is called a ball (or, more precisely a 3-ball).

The volume of the ball is given by

and the surface area of the sphere is Another type of sphere arises from a 4-ball, whose three-dimensional surface is the 3-sphere: points equidistant to the origin of the euclidean space R⁴. If a point has coordinates, P(x, y, z, w), then x² + y² + z² + w² = 1 characterizes those points on the unit 3-sphere centered at the origin.

This 3-sphere is an example of a 3-manifold: a space which is 'looks locally' like 3-D space. In precise topological terms, each point of the 3-sphere has a neighborhood which is homeomorphic to an open subset of 3-D space.

Polytopes

In three dimensions, there are nine regular polytopes: the five convex Platonic solids and the four nonconvex Kepler-Poinsot polyhedra.

Regular polytopes in three dimensions

Class	Platonic solids					Kepler-Poinsot polyhedra
Symmetry	Td	Oh		Ih
Coxeter group	A3,	B3,		H3,
Order	24	48		120
Regular polyhedron	{3,3}	{4,3}	{3,4}	{5,3}	{3,5}	{5/2,5}	{5,5/2}	{5/2,3}	{3,5/2}

Surfaces of revolution

A surface generated by revolving a plane curve about a fixed line in its plane as an axis is called a surface of revolution. The plane curve is called the generatrix of the surface. A section of the surface, made by intersecting the surface with a plane that is perpendicular (orthogonal) to the axis, is a circle.

Simple examples occur when the generatrix is a line. If the generatrix line intersects the axis line, the surface of revolution is a right circular cone with vertex (apex) the point of intersection. However, if the generatrix and axis are parallel, then the surface of revolution is a circular cylinder.

Quadric surfaces

In analogy with the conic sections, the set of points whose Cartesian coordinates satisfy the general equation of the second degree, namely,

where A, B, C, F, G, H, J, K, L and M are real numbers and not all of A, B, C, F, G and H are zero, is called a quadric surface.^[6]

There are six types of non-degenerate quadric surfaces:

1. Ellipsoid
2. Hyperboloid of one sheet
3. Hyperboloid of two sheets
4. Elliptic cone
5. Elliptic paraboloid
6. Hyperbolic paraboloid

The degenerate quadric surfaces are the empty set, a single point, a single line, a single plane, a pair of planes or a quadratic cylinder (a surface consisting of a non-degenerate conic section in a plane π and all the lines of R³ through that conic that are normal to π).^[6] Elliptic cones are sometimes considered to be degenerate quadric surfaces as well.

Both the hyperboloid of one sheet and the hyperbolic paraboloid are ruled surfaces, meaning that they can be made up from a family of straight lines. In fact, each has two families of generating lines, the members of each family are disjoint and each member one family intersects, with just one exception, every member of the other family.^[7] Each family is called a regulus.

In linear algebra

Another way of viewing three-dimensional space is found in linear algebra, where the idea of independence is crucial. Space has three dimensions because the length of a box is independent of its width or breadth. In the technical language of linear algebra, space is three-dimensional because every point in space can be described by a linear combination of three independent vectors.

Dot product, angle, and length

A vector can be pictured as an arrow. The vector's magnitude is its length, and its direction is the direction the arrow points. A vector in ${\displaystyle \mathbb {R} ^{3}}$ can be represented by an ordered triple of real numbers. These numbers are called the components of the vector.

The dot product of two vectors A = and B = is defined as:^[8]

${\displaystyle \mathbf {A} \cdot \mathbf {B} =A_{1}B_{1}+A_{2}B_{2}+A_{3}B_{3}=\sum _{i=1}^{3}A_{i}B_{i}.}$Zdroj:https://en.wikipedia.org?pojem=Three-dimensional
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---