In mathematics, the tangent space of a manifold is a generalization of tangent lines to curves in two-dimensional space and tangent planes to surfaces in three-dimensional space in higher dimensions. In the context of physics the tangent space to a manifold at a point can be viewed as the space of possible velocities for a particle moving on the manifold.

Informal description

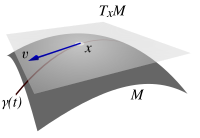
In differential geometry, one can attach to every point ${\displaystyle x}$ of a differentiable manifold a tangent space—a real vector space that intuitively contains the possible directions in which one can tangentially pass through ${\displaystyle x}$. The elements of the tangent space at ${\displaystyle x}$ are called the tangent vectors at ${\displaystyle x}$. This is a generalization of the notion of a vector, based at a given initial point, in a Euclidean space. The dimension of the tangent space at every point of a connected manifold is the same as that of the manifold itself.

For example, if the given manifold is a ${\displaystyle 2}$-sphere, then one can picture the tangent space at a point as the plane that touches the sphere at that point and is perpendicular to the sphere's radius through the point. More generally, if a given manifold is thought of as an embedded submanifold of Euclidean space, then one can picture a tangent space in this literal fashion. This was the traditional approach toward defining parallel transport. Many authors in differential geometry and general relativity use it.^[1][2] More strictly, this defines an affine tangent space, which is distinct from the space of tangent vectors described by modern terminology.

In algebraic geometry, in contrast, there is an intrinsic definition of the tangent space at a point of an algebraic variety ${\displaystyle V}$ that gives a vector space with dimension at least that of ${\displaystyle V}$ itself. The points ${\displaystyle p}$ at which the dimension of the tangent space is exactly that of ${\displaystyle V}$ are called non-singular points; the others are called singular points. For example, a curve that crosses itself does not have a unique tangent line at that point. The singular points of ${\displaystyle V}$ are those where the "test to be a manifold" fails. See Zariski tangent space.

Once the tangent spaces of a manifold have been introduced, one can define vector fields, which are abstractions of the velocity field of particles moving in space. A vector field attaches to every point of the manifold a vector from the tangent space at that point, in a smooth manner. Such a vector field serves to define a generalized ordinary differential equation on a manifold: A solution to such a differential equation is a differentiable curve on the manifold whose derivative at any point is equal to the tangent vector attached to that point by the vector field.

All the tangent spaces of a manifold may be "glued together" to form a new differentiable manifold with twice the dimension of the original manifold, called the tangent bundle of the manifold.

Formal definitions

The informal description above relies on a manifold's ability to be embedded into an ambient vector space ${\displaystyle \mathbb {R} ^{m}}$ so that the tangent vectors can "stick out" of the manifold into the ambient space. However, it is more convenient to define the notion of a tangent space based solely on the manifold itself.^[3]

There are various equivalent ways of defining the tangent spaces of a manifold. While the definition via the velocity of curves is intuitively the simplest, it is also the most cumbersome to work with. More elegant and abstract approaches are described below.

Definition via tangent curves

In the embedded-manifold picture, a tangent vector at a point ${\displaystyle x}$ is thought of as the velocity of a curve passing through the point ${\displaystyle x}$. We can therefore define a tangent vector as an equivalence class of curves passing through ${\displaystyle x}$ while being tangent to each other at ${\displaystyle x}$.

Suppose that ${\displaystyle M}$ is a ${\displaystyle C^{k}}$ differentiable manifold (with smoothness ${\displaystyle k\geq 1}$) and that ${\displaystyle x\in M}$. Pick a coordinate chart ${\displaystyle \varphi :U\to \mathbb {R} ^{n}}$, where ${\displaystyle U}$ is an open subset of ${\displaystyle M}$ containing ${\displaystyle x}$. Suppose further that two curves ${\displaystyle \gamma _{1},\gamma _{2}:(-1,1)\to M}$ with ${\displaystyle {\gamma _{1}}(0)=x={\gamma _{2}}(0)}$ are given such that both ${\displaystyle \varphi \circ \gamma _{1},\varphi \circ \gamma _{2}:(-1,1)\to \mathbb {R} ^{n}}$ are differentiable in the ordinary sense (we call these differentiable curves initialized at ${\displaystyle x}$). Then ${\displaystyle \gamma _{1}}$ and ${\displaystyle \gamma _{2}}$ are said to be equivalent at ${\displaystyle 0}$ if and only if the derivatives of ${\displaystyle \varphi \circ \gamma _{1}}$ and ${\displaystyle \varphi \circ \gamma _{2}}$ at ${\displaystyle 0}$ coincide. This defines an equivalence relation on the set of all differentiable curves initialized at ${\displaystyle x}$, and equivalence classes of such curves are known as tangent vectors of ${\displaystyle M}$ at ${\displaystyle x}$. The equivalence class of any such curve ${\displaystyle \gamma }$ is denoted by ${\displaystyle \gamma '(0)}$. The tangent space of ${\displaystyle M}$ at ${\displaystyle x}$, denoted by ${\displaystyle T_{x}M}$, is then defined as the set of all tangent vectors at ${\displaystyle x}$; it does not depend on the choice of coordinate chart ${\displaystyle \varphi :U\to \mathbb {R} ^{n}}$.

To define vector-space operations on ${\displaystyle T_{x}M}$, we use a chart ${\displaystyle \varphi :U\to \mathbb {R} ^{n}}$ and define a map ${\displaystyle \mathrm {d} {\varphi }_{x}:T_{x}M\to \mathbb {R} ^{n}}$ by $\mathrm{d}{\mathrm{\phi <!--\; \phi \; -->}}_x({\mathrm{\gamma <!--\; \gamma \; -->}}^{\prime }(0)):={\frac{\mathrm{d}}{\mathrm{d}t}}_{}$Zdroj:https://en.wikipedia.org?pojem=Tangent_space
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.