When a fluid flows around an object, the fluid exerts a force on the object. Lift is the component of this force that is perpendicular to the oncoming flow direction.^[1] It contrasts with the drag force, which is the component of the force parallel to the flow direction. Lift conventionally acts in an upward direction in order to counter the force of gravity, but it is defined to act perpendicular to the flow and therefore can act in any direction.

If the surrounding fluid is air, the force is called an aerodynamic force. In water or any other liquid, it is called a hydrodynamic force.

Dynamic lift is distinguished from other kinds of lift in fluids. Aerostatic lift or buoyancy, in which an internal fluid is lighter than the surrounding fluid, does not require movement and is used by balloons, blimps, dirigibles, boats, and submarines. Planing lift, in which only the lower portion of the body is immersed in a liquid flow, is used by motorboats, surfboards, windsurfers, sailboats, and water-skis.

Overview

A fluid flowing around the surface of a solid object applies a force on it. It does not matter whether the object is moving through a stationary fluid (e.g. an aircraft flying through the air) or whether the object is stationary and the fluid is moving (e.g. a wing in a wind tunnel) or whether both are moving (e.g. a sailboat using the wind to move forward). Lift is the component of this force that is perpendicular to the oncoming flow direction.^[1] Lift is always accompanied by a drag force, which is the component of the surface force parallel to the flow direction.

Lift is mostly associated with the wings of fixed-wing aircraft, although it is more widely generated by many other streamlined bodies such as propellers, kites, helicopter rotors, racing car wings, maritime sails, wind turbines, and by sailboat keels, ship's rudders, and hydrofoils in water. Lift is also used by flying and gliding animals, especially by birds, bats, and insects, and even in the plant world by the seeds of certain trees.^[2] While the common meaning of the word "lift" assumes that lift opposes weight, lift can be in any direction with respect to gravity, since it is defined with respect to the direction of flow rather than to the direction of gravity. When an aircraft is cruising in straight and level flight, most of the lift opposes gravity.^[3] However, when an aircraft is climbing, descending, or banking in a turn the lift is tilted with respect to the vertical.^[4] Lift may also act as downforce in some aerobatic manoeuvres, or on the wing on a racing car. Lift may also be largely horizontal, for instance on a sailing ship.

The lift discussed in this article is mainly in relation to airfoils, although marine hydrofoils and propellers share the same physical principles and work in the same way, despite differences between air and water such as density, compressibility, and viscosity.

The flow around a lifting airfoil is a fluid mechanics phenomenon that can be understood on essentially two levels: There are mathematical theories, which are based on established laws of physics and represent the flow accurately, but which require solving partial differential equations. And there are physical explanations without math, which are less rigorous.^[5] Correctly explaining lift in these qualitative terms is difficult because the cause-and-effect relationships involved are subtle.^[6] A comprehensive explanation that captures all of the essential aspects is necessarily complex. There are also many simplified explanations, but all leave significant parts of the phenomenon unexplained, while some also have elements that are simply incorrect.^{[5][7][8][9][10][11]}

Simplified physical explanations of lift on an airfoil

An airfoil is a streamlined shape that is capable of generating significantly more lift than drag.^[12] A flat plate can generate lift, but not as much as a streamlined airfoil, and with somewhat higher drag. Most simplified explanations follow one of two basic approaches, based either on Newton's laws of motion or on Bernoulli's principle.^{[5][13][14][15]}

Explanation based on flow deflection and Newton's laws

An airfoil generates lift by exerting a downward force on the air as it flows past. According to Newton's third law, the air must exert an equal and opposite (upward) force on the airfoil, which is lift.^{[16][17][18][19]}

As the airflow approaches the airfoil it is curving upward, but as it passes the airfoil it changes direction and follows a path that is curved downward. According to Newton's second law, this change in flow direction requires a downward force applied to the air by the airfoil. Then Newton's third law requires the air to exert an upward force on the airfoil; thus a reaction force, lift, is generated opposite to the directional change. In the case of an airplane wing, the wing exerts a downward force on the air and the air exerts an upward force on the wing.^{[20][21][22][23][24][25][excessive citations]}

The downward turning of the flow is not produced solely by the lower surface of the airfoil, and the air flow above the airfoil accounts for much of the downward-turning action.^{[26][27][28][29]}

This explanation is correct but it is incomplete. It does not explain how the airfoil can impart downward turning to a much deeper swath of the flow than it actually touches. Furthermore, it does not mention that the lift force is exerted by pressure differences, and does not explain how those pressure differences are sustained.^[5]

Controversy regarding the Coandă effect

Some versions of the flow-deflection explanation of lift cite the Coandă effect as the reason the flow is able to follow the convex upper surface of the airfoil. The conventional definition in the aerodynamics field is that the Coandă effect refers to the tendency of a fluid jet to stay attached to an adjacent surface that curves away from the flow, and the resultant entrainment of ambient air into the flow.^[30][31][32]

More broadly, some consider the effect to include the tendency of any fluid boundary layer to adhere to a curved surface, not just the boundary layer accompanying a fluid jet. It is in this broader sense that the Coandă effect is used by some popular references to explain why airflow remains attached to the top side of an airfoil.^[33][34] This is a controversial use of the term "Coandă effect"; the flow following the upper surface simply reflects an absence of boundary-layer separation, thus it is not an example of the Coandă effect.^{[35][36][37][38]} Regardless of whether this broader definition of the "Coandă effect" is applicable, calling it the "Coandă effect" does not provide an explanation, it just gives the phenomenon a name.^[39]

The ability of a fluid flow to follow a curved path is not dependent on shear forces, viscosity of the fluid, or the presence of a boundary layer. Air flowing around an airfoil, adhering to both upper and lower surfaces, and generating lift, is accepted as a phenomenon in inviscid flow.^[40]

Explanations based on an increase in flow speed and Bernoulli's principle

There are two common versions of this explanation, one based on "equal transit time", and one based on "obstruction" of the airflow.

False explanation based on equal transit-time

The "equal transit time" explanation starts by arguing that the flow over the upper surface is faster than the flow over the lower surface because the path length over the upper surface is longer and must be traversed in equal transit time.^[41][42][43] Bernoulli's principle states that under certain conditions increased flow speed is associated with reduced pressure. It is concluded that the reduced pressure over the upper surface results in upward lift.^[44]

A serious flaw in the equal transit time explanation is that it does not correctly explain what causes the flow to speed up.^[5] The longer-path-length explanation is simply wrong. No difference in path length is needed, and even when there is a difference, it is typically much too small to explain the observed speed difference.^[45] This is because the assumption of equal transit time is wrong. There is no physical principle that requires equal transit time and experimental results show that this assumption is false.^{[46][47][48][49][50][51]} In fact, the air moving over the top of an airfoil generating lift moves much faster than equal transit time predicts.^[52] The much higher flow speed over the upper surface can be clearly seen in this animated flow visualization.

Obstruction of the airflow

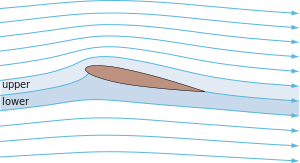
Like the equal transit time explanation, the "obstruction" or "streamtube pinching" explanation argues that the flow over the upper surface is faster than the flow over the lower surface, but gives a different reason for the difference in speed. It argues that the curved upper surface acts as more of an obstacle to the flow, forcing the streamlines to pinch closer together, making the streamtubes narrower. When streamtubes become narrower, conservation of mass requires that flow speed must increase.^[53] Reduced upper-surface pressure and upward lift follow from the higher speed by Bernoulli's principle, just as in the equal transit time explanation. Sometimes an analogy is made to a venturi nozzle, claiming the upper surface of the wing acts like a venturi nozzle to constrict the flow.^[54]

One serious flaw in the obstruction explanation is that it does not explain how streamtube pinching comes about, or why it is greater over the upper surface than the lower surface. For conventional wings that are flat on the bottom and curved on top this makes some intuitive sense, but it does not explain how flat plates, symmetric airfoils, sailboat sails, or conventional airfoils flying upside down can generate lift, and attempts to calculate lift based on the amount of constriction or obstruction do not predict experimental results.^{[55][56][57][58]} Another flaw is that conservation of mass is not a satisfying physical reason why the flow would speed up. Effectively explaining the acceleration of an object requires identifying the force that accelerates it.^[59]

Issues common to both versions of the Bernoulli-based explanation

A serious flaw common to all the Bernoulli-based explanations is that they imply that a speed difference can arise from causes other than a pressure difference, and that the speed difference then leads to a pressure difference, by Bernoulli's principle. This implied one-way causation is a misconception. The real relationship between pressure and flow speed is a mutual interaction.^[5] As explained below under a more comprehensive physical explanation, producing a lift force requires maintaining pressure differences in both the vertical and horizontal directions. The Bernoulli-only explanations do not explain how the pressure differences in the vertical direction are sustained. That is, they leave out the flow-deflection part of the interaction.^[5]

Although the two simple Bernoulli-based explanations above are incorrect, there is nothing incorrect about Bernoulli's principle or the fact that the air goes faster on the top of the wing, and Bernoulli's principle can be used correctly as part of a more complicated explanation of lift.^[60]

Basic attributes of lift

Lift is a result of pressure differences and depends on angle of attack, airfoil shape, air density, and airspeed.

Pressure differences

Pressure is the normal force per unit area exerted by the air on itself and on surfaces that it touches. The lift force is transmitted through the pressure, which acts perpendicular to the surface of the airfoil. Thus, the net force manifests itself as pressure differences. The direction of the net force implies that the average pressure on the upper surface of the airfoil is lower than the average pressure on the underside.^[61]

These pressure differences arise in conjunction with the curved airflow. When a fluid follows a curved path, there is a pressure gradient perpendicular to the flow direction with higher pressure on the outside of the curve and lower pressure on the inside.^[62] This direct relationship between curved streamlines and pressure differences, sometimes called the streamline curvature theorem, was derived from Newton's second law by Leonhard Euler in 1754:

${\displaystyle {\frac {\operatorname {d} p}{\operatorname {d} R}}=\rho {\frac {v^{2}}{R}}}$

The left side of this equation represents the pressure difference perpendicular to the fluid flow. On the right side of the equation, ρ is the density, v is the velocity, and R is the radius of curvature. This formula shows that higher velocities and tighter curvatures create larger pressure differentials and that for straight flow (R → ∞), the pressure difference is zero.^[63]

Angle of attack

The angle of attack is the angle between the chord line of an airfoil and the oncoming airflow. A symmetrical airfoil generates zero lift at zero angle of attack. But as the angle of attack increases, the air is deflected through a larger angle and the vertical component of the airstream velocity increases, resulting in more lift. For small angles, a symmetrical airfoil generates a lift force roughly proportional to the angle of attack.^[64][65]

As the angle of attack increases, the lift reaches a maximum at some angle; increasing the angle of attack beyond this critical angle of attack causes the upper-surface flow to separate from the wing; there is less deflection downward so the airfoil generates less lift. The airfoil is said to be stalled.^[66]

Airfoil shape

The maximum lift force that can be generated by an airfoil at a given airspeed depends on the shape of the airfoil, especially the amount of camber (curvature such that the upper surface is more convex than the lower surface, as illustrated at right). Increasing the camber generally increases the maximum lift at a given airspeed.^[67][68]

Cambered airfoils generate lift at zero angle of attack. When the chord line is horizontal, the trailing edge has a downward direction and since the air follows the trailing edge it is deflected downward.^[69] When a cambered airfoil is upside down, the angle of attack can be adjusted so that the lift force is upward. This explains how a plane can fly upside down.^[70][71]

Flow conditions

The ambient flow conditions which affect lift include the fluid density, viscosity and speed of flow. Density is affected by temperature, and by the medium's acoustic velocity – i.e. by compressibility effects.

Air speed and density

Lift is proportional to the density of the air and approximately proportional to the square of the flow speed. Lift also depends on the size of the wing, being generally proportional to the wing's area projected in the lift direction. In calculations it is convenient to quantify lift in terms of a lift coefficient based on these factors.

Boundary layer and profile drag

No matter how smooth the surface of an airfoil seems, any surface is rough on the scale of air molecules. Air molecules flying into the surface bounce off the rough surface in random directions relative to their original velocities. The result is that when the air is viewed as a continuous material, it is seen to be unable to slide along the surface, and the air's velocity relative to the airfoil decreases to nearly zero at the surface (i.e., the air molecules "stick" to the surface instead of sliding along it), something known as the no-slip condition.^[72] Because the air at the surface has near-zero velocity but the air away from the surface is moving, there is a thin boundary layer in which air close to the surface is subjected to a shearing motion.^[73][74] The air's viscosity resists the shearing, giving rise to a shear stress at the airfoil's surface called skin friction drag. Over most of the surface of most airfoils, the boundary layer is naturally turbulent, which increases skin friction drag.^[74][75]

Under usual flight conditions, the boundary layer remains attached to both the upper and lower surfaces all the way to the trailing edge, and its effect on the rest of the flow is modest. Compared to the predictions of inviscid flow theory, in which there is no boundary layer, the attached boundary layer reduces the lift by a modest amount and modifies the pressure distribution somewhat, which results in a viscosity-related pressure drag over and above the skin friction drag. The total of the skin friction drag and the viscosity-related pressure drag is usually called the profile drag.^[75][76]

Stalling

An airfoil's maximum lift at a given airspeed is limited by boundary-layer separation. As the angle of attack is increased, a point is reached where the boundary layer can no longer remain attached to the upper surface. When the boundary layer separates, it leaves a region of recirculating flow above the upper surface, as illustrated in the flow-visualization photo at right. This is known as the stall, or stalling. At angles of attack above the stall, lift is significantly reduced, though it does not drop to zero. The maximum lift that can be achieved before stall, in terms of the lift coefficient, is generally less than 1.5 for single-element airfoils and can be more than 3.0 for airfoils with high-lift slotted flaps and leading-edge devices deployed.^[77]

Bluff bodies

The flow around bluff bodies – i.e. without a streamlined shape, or stalling airfoils – may also generate lift, in addition to a strong drag force. This lift may be steady, or it may oscillate due to vortex shedding. Interaction of the object's flexibility with the vortex shedding may enhance the effects of fluctuating lift and cause vortex-induced vibrations.^[78] For instance, the flow around a circular cylinder generates a Kármán vortex street: vortices being shed in an alternating fashion from the cylinder's sides. The oscillatory nature of the flow produces a fluctuating lift force on the cylinder, even though the net (mean) force is negligible. The lift force frequency is characterised by the dimensionless Strouhal number, which depends on the Reynolds number of the flow.^[79][80]

For a flexible structure, this oscillatory lift force may induce vortex-induced vibrations. Under certain conditions – for instance resonance or strong spanwise correlation of the lift force – the resulting motion of the structure due to the lift fluctuations may be strongly enhanced. Such vibrations may pose problems and threaten collapse in tall man-made structures like industrial chimneys.^[78]

In the Magnus effect, a lift force is generated by a spinning cylinder in a freestream. Here the mechanical rotation acts on the boundary layer, causing it to separate at different locations on the two sides of the cylinder. The asymmetric separation changes the effective shape of the cylinder as far as the flow is concerned such that the cylinder acts like a lifting airfoil with circulation in the outer flow.^[81]

A more comprehensive physical explanation

As described above under "Simplified physical explanations of lift on an airfoil", there are two main popular explanations: one based on downward deflection of the flow (Newton's laws), and one based on pressure differences accompanied by changes in flow speed (Bernoulli's principle). Either of these, by itself, correctly identifies some aspects of the lifting flow but leaves other important aspects of the phenomenon unexplained. A more comprehensive explanation involves both downward deflection and pressure differences (including changes in flow speed associated with the pressure differences), and requires looking at the flow in more detail.^[82]

Lift at the airfoil surface

The airfoil shape and angle of attack work together so that the airfoil exerts a downward force on the air as it flows past. According to Newton's third law, the air must then exert an equal and opposite (upward) force on the airfoil, which is the lift.^[18]

The net force exerted by the air occurs as a pressure difference over the airfoil's surfaces.^[83] Pressure in a fluid is always positive in an absolute sense,^[84] so that pressure must always be thought of as pushing, and never as pulling. The pressure thus pushes inward on the airfoil everywhere on both the upper and lower surfaces. The flowing air reacts to the presence of the wing by reducing the pressure on the wing's upper surface and increasing the pressure on the lower surface. The pressure on the lower surface pushes up harder than the reduced pressure on the upper surface pushes down, and the net result is upward lift.^[83]

The pressure difference which results in lift acts directly on the airfoil surfaces; however, understanding how the pressure difference is produced requires understanding what the flow does over a wider area.

The wider flow around the airfoil

An airfoil affects the speed and direction of the flow over a wide area, producing a pattern called a velocity field. When an airfoil produces lift, the flow ahead of the airfoil is deflected upward, the flow above and below the airfoil is deflected downward leaving the air far behind the airfoil in the same state as the oncoming flow far ahead. The flow above the upper surface is sped up, while the flow below the airfoil is slowed down. Together with the upward deflection of air in front and the downward deflection of the air immediately behind, this establishes a net circulatory component of the flow. The downward deflection and the changes in flow speed are pronounced and extend over a wide area, as can be seen in the flow animation on the right. These differences in the direction and speed of the flow are greatest close to the airfoil and decrease gradually far above and below. All of these features of the velocity field also appear in theoretical models for lifting flows.^[85][86]

The pressure is also affected over a wide area, in a pattern of non-uniform pressure called a pressure field. When an airfoil produces lift, there is a diffuse region of low pressure above the airfoil, and usually a diffuse region of high pressure below, as illustrated by the isobars (curves of constant pressure) in the drawing. The pressure difference that acts on the surface is just part of this pressure field.^[87]

Mutual interaction of pressure differences and changes in flow velocity

The non-uniform pressure exerts forces on the air in the direction from higher pressure to lower pressure. The direction of the force is different at different locations around the airfoil, as indicated by the block arrows in the pressure field around an airfoil figure. Air above the airfoil is pushed toward the center of the low-pressure region, and air below the airfoil is pushed outward from the center of the high-pressure region.

According to Newton's second law, a force causes air to accelerate in the direction of the force. Thus the vertical arrows in the accompanying pressure field diagram indicate that air above and below the airfoil is accelerated, or turned downward, and that the non-uniform pressure is thus the cause of the downward deflection of the flow visible in the flow animation. To produce this downward turning, the airfoil must have a positive angle of attack or have sufficient positive camber. Note that the downward turning of the flow over the upper surface is the result of the air being pushed downward by higher pressure above it than below it. Some explanations that refer to the "Coandă effect" suggest that viscosity plays a key role in the downward turning, but this is false. (see above under "Controversy regarding the Coandă effect").

The arrows ahead of the airfoil indicate that the flow ahead of the airfoil is deflected upward, and the arrows behind the airfoil indicate that the flow behind is deflected upward again, after being deflected downward over the airfoil. These deflections are also visible in the flow animation.

The arrows ahead of the airfoil and behind also indicate that air passing through the low-pressure region above the airfoil is sped up as it enters, and slowed back down as it leaves. Air passing through the high-pressure region below the airfoil is slowed down as it enters and then sped back up as it leaves. Thus the non-uniform pressure is also the cause of the changes in flow speed visible in the flow animation. The changes in flow speed are consistent with Bernoulli's principle, which states that in a steady flow without viscosity, lower pressure means higher speed, and higher pressure means lower speed.

Thus changes in flow direction and speed are directly caused by the non-uniform pressure. But this cause-and-effect relationship is not just one-way; it works in both directions simultaneously. The air's motion is affected by the pressure differences, but the existence of the pressure differences depends on the air's motion. The relationship is thus a mutual, or reciprocal, interaction: Air flow changes speed or direction in response to pressure differences, and the pressure differences are sustained by the air's resistance to changing speed or direction.^[88] A pressure difference can exist only if something is there for it to push against. In aerodynamic flow, the pressure difference pushes against the air's inertia, as the air is accelerated by the pressure difference.^[89] This is why the air's mass is part of the calculation, and why lift depends on air density.

Sustaining the pressure difference that exerts the lift force on the airfoil surfaces requires sustaining a pattern of non-uniform pressure in a wide area around the airfoil. This requires maintaining pressure differences in both the vertical and horizontal directions, and thus requires both downward turning of the flow and changes in flow speed according to Bernoulli's principle. The pressure differences and the changes in flow direction and speed sustain each other in a mutual interaction. The pressure differences follow naturally from Newton's second law and from the fact that flow along the surface follows the predominantly downward-sloping contours of the airfoil. And the fact that the air has mass is crucial to the interaction.^[90]

How simpler explanations fall short

Producing a lift force requires both downward turning of the flow and changes in flow speed consistent with Bernoulli's principle. Each of the simplified explanations given above in Simplified physical explanations of lift on an airfoil falls short by trying to explain lift in terms of only one or the other, thus explaining only part of the phenomenon and leaving other parts unexplained.^[91]

Quantifying lift

Pressure integration

When the pressure distribution on the airfoil surface is known, determining the total lift requires adding up the contributions to the pressure force from local elements of the surface, each with its own local value of pressure. The total lift is thus the integral of the pressure, in the direction perpendicular to the farfield flow, over the airfoil surface.^[92]

${\displaystyle L=\oint p\mathbf {n} \cdot \mathbf {k} \;\mathrm {d} S,}$

where:

• S is the projected (planform) area of the airfoil, measured normal to the mean airflow;
• n is the normal unit vector pointing into the wing;
• k is the vertical unit vector, normal to the freestream direction.

The above lift equation neglects the skin friction forces, which are small compared to the pressure forces.

By using the streamwise vector i parallel to the freestream in place of k in the integral, we obtain an expression for the pressure drag D_p (which includes the pressure portion of the profile drag and, if the wing is three-dimensional, the induced drag). If we use the spanwise vector j, we obtain the side force Y.

${\displaystyle {\begin{aligned}D_{p}&=\oint p\mathbf {n} \cdot \mathbf {i} \;\mathrm {d} S,\\Y&=\oint p\mathbf {n} \cdot \mathbf {j} \;\mathrm {d} S.\end{aligned}}}$

The validity of this integration generally requires the airfoil shape to be a closed curve that is piecewise smooth.

Lift coefficientedit

Lift depends on the size of the wing, being approximately proportional to the wing area. It is often convenient to quantify the lift of a given airfoil by its lift coefficient ${\displaystyle C_{L}}$, which defines its overall lift in terms of a unit area of the wing.

If the value of ${\displaystyle C_{L}}$ for a wing at a specified angle of attack is given, then the lift produced for specific flow conditions can be determined:^[93]

${\displaystyle L={\tfrac {1}{2}}\rho v^{2}SC_{L}}$

where

• ${\displaystyle L}$ is the lift force
• ${\displaystyle \rho }$Zdroj:https://en.wikipedia.org?pojem=Lift_(force)
  Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

  ---