
A | B | C | D | E | F | G | H | CH | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
| Part of a series on |
| Numeral systems |
|---|
| List of numeral systems |
In mathematics and computing, the hexadecimal (also base-16 or simply hex) numeral system is a positional numeral system that represents numbers using a radix (base) of sixteen. Unlike the decimal system representing numbers using ten symbols, hexadecimal uses sixteen distinct symbols, most often the symbols "0"–"9" to represent values 0 to 9 and "A"–"F" (or "a"–"f") to represent values from ten to fifteen.
Software developers and system designers widely use hexadecimal numbers because they provide a human-friendly representation of binary-coded values. Each hexadecimal digit represents four bits (binary digits), also known as a nibble (or nybble).[1] For example, an 8-bit byte can have values ranging from 00000000 to 11111111 (0 to 255 decimal) in binary form, which can be conveniently represented as 00 to FF in hexadecimal.
In mathematics, a subscript is typically used to specify the base. For example, the decimal value 33,319 would be expressed in hexadecimal as 822716. In programming, several notations denote hexadecimal numbers, usually involving a prefix. The prefix 0x is used in C, which would denote this value as 0x8227.
Hexadecimal is used in the transfer encoding Base 16, in which each byte of the plain text is broken into two 4-bit values and represented by two hexadecimal digits.
Representation
Written representation
In most current use cases, the letters A–F or a–f represent the values 10–15, while the numerals 0–9 are used to represent their decimal values.
There is no universal convention to use lowercase or uppercase, so each is prevalent or preferred in particular environments by community standards or convention; even mixed case is used. Some Seven-segment displays use mixed-case 'A b C d E F' to distinguish the digits A–F from one another and from 0–9.
There is some standardization of using spaces (rather than commas or another punctuation mark) to separate hex values in a long list. For instance, in the following hex dump, each 8-bit byte is a 2-digit hex number, with spaces between them, while the 32-bit offset at the start is an 8-digit hex number.
00000000 57 69 6b 69 70 65 64 69 61 2c 20 74 68 65 20 66
00000010 72 65 65 20 65 6e 63 79 63 6c 6f 70 65 64 69 61
00000020 20 74 68 61 74 20 61 6e 79 6f 6e 65 20 63 61 6e
00000030 20 65 64 69 74 0a
Distinguishing from decimal
In contexts where the base is not clear, hexadecimal numbers can be ambiguous and confused with numbers expressed in other bases. There are several conventions for expressing values unambiguously. A numerical subscript (itself written in decimal) can give the base explicitly: 15910 is decimal 159; 15916 is hexadecimal 159, which equals 34510. Some authors prefer a text subscript, such as 159decimal and 159hex, or 159d and 159h.
Donald Knuth introduced the use of a particular typeface to represent a particular radix in his book The TeXbook.[2] Hexadecimal representations are written there in a typewriter typeface: 5A3, C1F27ED
In linear text systems, such as those used in most computer programming environments, a variety of methods have arisen:
- Unix (and related) shells, AT&T assembly language and likewise the C programming language (and its syntactic descendants such as C++, C#, Go, D, Java, JavaScript, Python and Windows PowerShell) use the prefix
0xfor numeric constants represented in hex:0x5A3,0xC1F27ED. Character and string constants may express character codes in hexadecimal with the prefix\xfollowed by two hex digits:'\x1B'represents the Esc control character;"\x1B25;1H"is a string containing 11 characters with two embedded Esc characters.[3] To output an integer as hexadecimal with the printf function family, the format conversion code%Xor%xis used. - In XML and XHTML, characters can be expressed as hexadecimal numeric character references using the notation
ode;, for instanceTrepresents the character U+0054 (the uppercase letter "T"). If there is noxthe number is decimal (thusTis the same character).[4] - In Intel-derived assembly languages and Modula-2,[5] hexadecimal is denoted with a suffixed H or h:
FFhor05A3H. Some implementations require a leading zero when the first hexadecimal digit character is not a decimal digit, so one would write0FFhinstead ofFFh. Some other implementations (such as NASM) allow C-style numbers (0x42). - Other assembly languages (6502, Motorola), Pascal, Delphi, some versions of BASIC (Commodore), GameMaker Language, Godot and Forth use
$as a prefix:$5A3,$C1F27ED. - Some assembly languages (Microchip) use the notation
H'ABCD'(for ABCD16). Similarly, Fortran 95 uses Z'ABCD'. - Ada and VHDL enclose hexadecimal numerals in based "numeric quotes":
16#5A3#,16#C1F27ED#. For bit vector constants VHDL uses the notationx"5A3",x"C1F27ED".[6] - Verilog represents hexadecimal constants in the form
8'hFF, where 8 is the number of bits in the value and FF is the hexadecimal constant. - The Icon and Smalltalk languages use the prefix
16r:16r5A3 - PostScript and the Bourne shell and its derivatives denote hex with prefix
16#:16#5A3,16#C1F27ED. - Common Lisp uses the prefixes
#xand#16r. Setting the variables *read-base*[7] and *print-base*[8] to 16 can also be used to switch the reader and printer of a Common Lisp system to Hexadecimal number representation for reading and printing numbers. Thus Hexadecimal numbers can be represented without the #x or #16r prefix code, when the input or output base has been changed to 16. - MSX BASIC,[9] QuickBASIC, FreeBASIC and Visual Basic prefix hexadecimal numbers with
&H:&H5A3 - BBC BASIC and Locomotive BASIC use
&for hex.[10] - TI-89 and 92 series uses a
0hprefix:0h5A3,0hC1F27ED - ALGOL 68 uses the prefix
16rto denote hexadecimal numbers:16r5a3,16rC1F27ED. Binary, quaternary (base-4), and octal numbers can be specified similarly. - The most common format for hexadecimal on IBM mainframes (zSeries) and midrange computers (IBM i) running the traditional OS's (zOS, zVSE, zVM, TPF, IBM i) is
X'5A3'orX'C1F27ED', and is used in Assembler, PL/I, COBOL, JCL, scripts, commands and other places. This format was common on other (and now obsolete) IBM systems as well. Occasionally quotation marks were used instead of apostrophes.
Syntax that is always Hexedit
Sometimes the numbers are known to be Hex.
- In URIs (including URLs), character codes are written as hexadecimal pairs prefixed with
%:http://www.example.com/name%20with%20spaceswhere%20is the code for the space (blank) character, ASCII code point 20 in hex, 32 in decimal. - In the Unicode standard, a character value is represented with
U+followed by the hex value, e.g.U+00A1is the inverted exclamation point (¡). - Color references in HTML, CSS and X Window can be expressed with six hexadecimal digits (two each for the red, green and blue components, in that order) prefixed with
#: magenta, for example, is represented as#FF00FF.[11] CSS also allows 3-hexdigit abbreviations with one hexdigit per component:#FA3abbreviates#FFAA33(a golden orange: ). - In MIME (e-mail extensions) quoted-printable encoding, character codes are written as hexadecimal pairs prefixed with
=:Espa=F1ais "España" (F1hex is the code for ñ in the ISO/IEC 8859-1 character set).[12]) - PostScript binary data (such as image pixels) can be expressed as unprefixed consecutive hexadecimal pairs:
AA213FD51B3801043FBC... - Any IPv6 address can be written as eight groups of four hexadecimal digits (sometimes called hextets), where each group is separated by a colon (
:). This, for example, is a valid IPv6 address:2001:0db8:85a3:0000:0000:8a2e:0370:7334or abbreviated by removing leading zeros as2001:db8:85a3::8a2e:370:7334(IPv4 addresses are usually written in decimal). - Globally unique identifiers are written as thirty-two hexadecimal digits, often in unequal hyphen-separated groupings, for example
3F2504E0-4F89-41D3-9A0C-0305E82C3301.
Other symbols for 10–15 and mostly different symbol setsedit
The use of the letters A through F to represent the digits above 9 was not universal in the early history of computers.
- During the 1950s, some installations, such as Bendix-14, favored using the digits 0 through 5 with an overline to denote the values 10–15 as 0, 1, 2, 3, 4 and 5.
- The SWAC (1950)[13] and Bendix G-15 (1956)[14][13] computers used the lowercase letters u, v, w, x, y and z for the values 10 to 15.
- The ORDVAC and ILLIAC I (1952) computers (and some derived designs, e.g. BRLESC) used the uppercase letters K, S, N, J, F and L for the values 10 to 15.[15][13]
- The Librascope LGP-30 (1956) used the letters F, G, J, K, Q and W for the values 10 to 15.[16][13]
- On the PERM (1956) computer, hexadecimal numbers were written as letters O for zero, A to N and P for 1 to 15. Many machine instructions had mnemonic hex-codes (A=add, M=multiply, L=load, F=fixed-point etc.); programs were written without instruction names.[17]
- The Honeywell Datamatic D-1000 (1957) used the lowercase letters b, c, d, e, f, and g whereas the Elbit 100 (1967) used the uppercase letters B, C, D, E, F and G for the values 10 to 15.[13]
- The Monrobot XI (1960) used the letters S, T, U, V, W and X for the values 10 to 15.[13]
- The NEC parametron computer NEAC 1103 (1960) used the letters D, G, H, J, K (and possibly V) for values 10–15.[18]
- The Pacific Data Systems 1020 (1964) used the letters L, C, A, S, M and D for the values 10 to 15.[13]

- New numeric symbols and names were introduced in the Bibi-binary notation by Boby Lapointe in 1968.
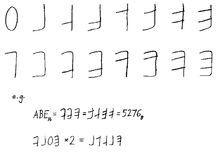
- Bruce Alan Martin of Brookhaven National Laboratory considered the choice of A–F "ridiculous". In a 1968 letter to the editor of the CACM, he proposed an entirely new set of symbols based on the bit locations.[19]

- In 1972, Ronald O. Whitaker of Rowco Engineering Co. proposed a triangular font that allows "direct binary reading" to "permit both input and output from computers without respect to encoding matrices."[20][21]
- Some seven-segment display decoder chips (i.e., 74LS47) show unexpected output due to logic designed only to produce 0–9 correctly.[22]
Verbal and digital representationsedit
Since there were no traditional numerals to represent the quantities from ten to fifteen, alphabetic letters were re-employed as a substitute. Most European languages lack non-decimal-based words for some of the numerals eleven to fifteen. Some people read hexadecimal numbers digit by digit, like a phone number, or using the NATO phonetic alphabet, the Joint Army/Navy Phonetic Alphabet, or a similar ad-hoc system. In the wake of the adoption of hexadecimal among IBM System/360 programmers, Magnuson (1968)[23] suggested a pronunciation guide that gave short names to the letters of hexadecimal – for instance, "A" was pronounced "ann", B "bet", C "chris", etc.[23] Another naming-system was published online by Rogers (2007)[24] that tries to make the verbal representation distinguishable in any case, even when the actual number does not contain numbers A–F. Examples are listed in the tables below. Yet another naming system was elaborated by Babb (2015), based on a joke in Silicon Valley.[25]
Others have proposed using the verbal Morse Code conventions to express four-bit hexadecimal digits, with "dit" and "dah" representing zero and one, respectively, so that "0000" is voiced as "dit-dit-dit-dit" (....), dah-dit-dit-dah (-..-) voices the digit with a value of nine, and "dah-dah-dah-dah" (----) voices the hexadecimal digit for decimal 15.

Systems of counting on digits have been devised for both binary and hexadecimal. Arthur C. Clarke suggested using each finger as an on/off bit, allowing finger counting from zero to 102310 on ten fingers.[26] Another system for counting up to FF16 (25510) is illustrated on the right.
| Number | Pronunciation |
|---|---|
| A | ann |
| B | bet |
| C | chris |
| D | dot |
| E | ernest |
| F | frost |
| 1A | annteen |
| A0 | annty |
| 5B | fifty-bet |
| A01C | annty christeen |
| 1AD0 | annteen dotty |
| 3A7D | thirty-ann seventy-dot |
| Number | Pronunciation |
|---|---|
| A | ten |
| B | eleven |
| C | twelve |
| D | draze |
| E | eptwin |
| F | fim |
| 10 | tex |
| 11 | oneteek |
| 1F | fimteek |
| 50 | fiftek |
| C0 | twelftek |
| 100 | hundrek |
| 1000 | thousek |
| 3E | thirtek-eptwin |
| E1 | eptek-one |
| C4A | twelve-hundrek-fourtek-ten |
| 1743 | one-thousek-seven- -hundrek-fourtek-three |
Signsedit
The hexadecimal system can express negative numbers the same way as in decimal: −2A to represent −4210, −B01D9 to represent −72136910 and so on.
Hexadecimal can also be used to express the exact bit patterns used in the processor, so a sequence of hexadecimal digits may represent a signed or even a floating-point value. This way, the negative number −4210 can be written as FFFF FFD6 in a 32-bit CPU register (in two's complement), as C228 0000 in a 32-bit FPU register or C045 0000 0000 0000 in a 64-bit FPU register (in the IEEE floating-point standard).
Hexadecimal exponential notationedit
Just as decimal numbers can be represented in exponential notation, so too can hexadecimal numbers. P notation uses the letter P (or p, for "power"), whereas E (or e) serves a similar purpose in decimal E notation. The number after the P is decimal and represents the binary exponent. Increasing the exponent by 1 multiplies by 2, not 16: 20p0 = 10p1 = 8p2 = 4p3 = 2p4 = 1p5. Usually, the number is normalized so that the hexadecimal digits start with 1. (zero is usually 0 with no P).
Example: 1.3DEp42 represents 1.3DE16 × 24210.
P notation is required by the IEEE 754-2008 binary floating-point standard and can be used for floating-point literals in the C99 edition of the C programming language.[27] Using the %a or %A conversion specifiers, this notation can be produced by implementations of the printf family of functions following the C99 specification[28] and Single Unix Specification (IEEE Std 1003.1) POSIX standard.[29]
Conversionedit
Binary conversionedit

Most computers manipulate binary data, but it is difficult for humans to work with a large number of digits for even a relatively small binary number. Although most humans are familiar with the base 10 system, it is much easier to map binary to hexadecimal than to decimal because each hexadecimal digit maps to a whole number of bits (410). This example converts 11112 to base ten. Since each position in a binary numeral can contain either a 1 or a 0, its value may be easily determined by its position from the right:
- 00012 = 110
- 00102 = 210
- 01002 = 410
- 10002 = 810
Therefore:
| 11112 | = 810 + 410 + 210 + 110 |
| = 1510 |
With little practice, mapping 11112 to F16 in one step becomes easy (see table in written representation). The advantage of using hexadecimal rather than decimal increases rapidly with the size of the number. When the number becomes large, conversion to decimal is very tedious. However, when mapping to hexadecimal, it is trivial to regard the binary string as 4-digit groups and map each to a single hexadecimal digit.[30]
This example shows the conversion of a binary number to decimal, mapping each digit to the decimal value, and adding the results.
| (1001011100)2 | = 51210 + 6410 + 1610 + 810 + 410 |
| = 60410 |
Compare this to the conversion to hexadecimal, where each group of four digits can be considered independently and converted directly:
| (1001011100)2 | = | 0010 | 0101 | 11002 | ||
| = | 2 | 5 | C16 | |||
| = | 25C16 | |||||
The conversion from hexadecimal to binary is equally direct.[30]
Other simple conversionsedit
Although quaternary (base 4) is little used, it can easily be converted to and from hexadecimal or binary. Each hexadecimal digit corresponds to a pair of quaternary digits, and each quaternary digit corresponds to a pair of binary digits. In the above example 2 5 C16 = 02 11 304.
The octal (base 8) system can also be converted with relative ease, although not quite as trivially as with bases 2 and 4. Each octal digit corresponds to three binary digits, rather than four. Therefore, we can convert between octal and hexadecimal via an intermediate conversion to binary followed by regrouping the binary digits in groups of either three or four.
Division-remainder in source baseedit
As with all bases there is a simple algorithm for converting a representation of a number to hexadecimal by doing integer division and remainder operations in the source base. In theory, this is possible from any base, but for most humans, only decimal and for most computers, only binary (which can be converted by far more efficient methods) can be easily handled with this method.
Let d be the number to represent in hexadecimal, and the series hihi−1...h2h1 be the hexadecimal digits representing the number.
- i ← 1
- hi ← d mod 16
- d ← (d − hi) / 16
- If d = 0 (return series hi) else increment i and go to step 2
"16" may be replaced with any other base that may be desired.
The following is a JavaScript implementation of the above algorithm for converting any number to a hexadecimal in String representation. Its purpose is to illustrate the above algorithm. To work with data seriously, however, it is much more advisable to work with bitwise operators.
function toHex(d) {
var r = d % 16;
if (d - r == 0) {
return toChar(r);
}
return toHex((d - r) / 16) + toChar(r);
}
function toChar(n) {
const alpha = "0123456789ABCDEF";
return alpha.charAt(n);
}
Conversion through addition and multiplicationedit

It is also possible to make the conversion by assigning each place in the source base the hexadecimal representation of its place value — before carrying out multiplication and addition to get the final representation. For example, to convert the number B3AD to decimal, one can split the hexadecimal number into its digits: B (1110), 3 (310), A (1010) and D (1310), and then get the final result by multiplying each decimal representation by 16p (p being the corresponding hex digit position, counting from right to left, beginning with 0). In this case, we have that:
B3AD = (11 × 163) + (3 × 162) + (10 × 161) + (13 × 160)
which is 45997 in base 10.
Tools for conversionedit
Many computer systems provide a calculator utility capable of performing conversions between the various radices frequently including hexadecimal.
In Microsoft Windows, the Calculator utility can be set to Programmer mode, which allows conversions between radix 16 (hexadecimal), 10 (decimal), 8 (octal), and 2 (binary), the bases most commonly used by programmers. In Programmer Mode, the on-screen numeric keypad includes the hexadecimal digits A through F, which are active when "Hex" is selected. In hex mode, however, the Windows Calculator supports only integers.
Elementary arithmeticedit
Elementary operations such as division can be carried out indirectly through conversion to an alternate numeral system, such as the commonly used decimal system or the binary system where each hex digit corresponds to four binary digits.
Alternatively, one can also perform elementary operations directly within the hex system itself — by relying on its addition/multiplication tables and its corresponding standard algorithms such as long division and the traditional subtraction algorithm.
Real numbersedit
Rational numbersedit
As with other numeral systems, the hexadecimal system can be used to represent rational numbers, although repeating expansions are common since sixteen (1016) has only a single prime factor: two.
For any base, 0.1 (or "1/10") is always equivalent to one divided by the representation of that base value in its own number system. Thus, whether dividing one by two for binary or dividing one by sixteen for hexadecimal, both of these fractions are written as 0.1. Because the radix 16 is a perfect square (42), fractions expressed in hexadecimal have an odd period much more often than decimal ones, and there are no cyclic numbers (other than trivial single digits). Recurring digits are exhibited when the denominator in lowest terms has a prime factor not found in the radix; thus, when using hexadecimal notation, all fractions with denominators that are not a power of two result in an infinite string of recurring digits (such as thirds and fifths). This makes hexadecimal (and binary) less convenient than decimal for representing rational numbers since a larger proportion lies outside its range of finite representation.
All rational numbers finitely representable in hexadecimal are also finitely representable in decimal, duodecimal and sexagesimal: that is, any hexadecimal number with a finite number of digits also has a finite number of digits when expressed in those other bases. Conversely, only a fraction of those finitely representable in the latter bases are finitely representable in hexadecimal. For example, decimal 0.1 corresponds to the infinite recurring representation 0.19 in hexadecimal. However, hexadecimal is more efficient than duodecimal and sexagesimal for representing fractions with powers of two in the denominator. For example, 0.062510 (one-sixteenth) is equivalent to 0.116, 0.0912, and 0;3,4560.
| n | Decimal Prime factors of: base, b = 10: 2, 5; b − 1 = 9: 3 |
Hexadecimal Prime factors of: base, b = 1610 = 10: 2; b − 1 = 1510 = F: 3, 5 | ||||
|---|---|---|---|---|---|---|
| Reciprocal | Prime factors | Positional representation (decimal) |
Positional representation (hexadecimal) |
Prime factors | Reciprocal | |
| 2 | 1/2 | 2 | 0.5 | 0.8 | 2 | 1/2 |
| 3 | 1/3 | 3 | 0.3333... = 0.3 | 0.5555... = 0.5 | 3 | 1/3 |
| 4 | 1/4 | 2 | 0.25 | 0.4 | 2 | 1/4 |
| 5 | 1/5 | 5 | 0.2 | 0.3 | 5 | 1/5 |
| 6 | 1/6 | 2, 3 | 0.16 | 0.2A | 2, 3 | 1/6 |
| 7 | 1/7 | 7 | 0.142857 | 0.249 | 7 | 1/7 |
| 8 | 1/8 | 2 | 0.125 | 0.2 | 2 | 1/8 |
