In geometry, curvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is locally invertible (a one-to-one map) at each point. This means that one can convert a point given in a Cartesian coordinate system to its curvilinear coordinates and back. The name curvilinear coordinates, coined by the French mathematician Lamé, derives from the fact that the coordinate surfaces of the curvilinear systems are curved.

Well-known examples of curvilinear coordinate systems in three-dimensional Euclidean space (R³) are cylindrical and spherical coordinates. A Cartesian coordinate surface in this space is a coordinate plane; for example z = 0 defines the x-y plane. In the same space, the coordinate surface r = 1 in spherical coordinates is the surface of a unit sphere, which is curved. The formalism of curvilinear coordinates provides a unified and general description of the standard coordinate systems.

Curvilinear coordinates are often used to define the location or distribution of physical quantities which may be, for example, scalars, vectors, or tensors. Mathematical expressions involving these quantities in vector calculus and tensor analysis (such as the gradient, divergence, curl, and Laplacian) can be transformed from one coordinate system to another, according to transformation rules for scalars, vectors, and tensors. Such expressions then become valid for any curvilinear coordinate system.

A curvilinear coordinate system may be simpler to use than the Cartesian coordinate system for some applications. The motion of particles under the influence of central forces is usually easier to solve in spherical coordinates than in Cartesian coordinates; this is true of many physical problems with spherical symmetry defined in R³. Equations with boundary conditions that follow coordinate surfaces for a particular curvilinear coordinate system may be easier to solve in that system. While one might describe the motion of a particle in a rectangular box using Cartesian coordinates, it is easier to describe the motion in a sphere with spherical coordinates. Spherical coordinates are the most common curvilinear coordinate systems and are used in Earth sciences, cartography, quantum mechanics, relativity, and engineering.

Orthogonal curvilinear coordinates in 3 dimensions

Coordinates, basis, and vectors

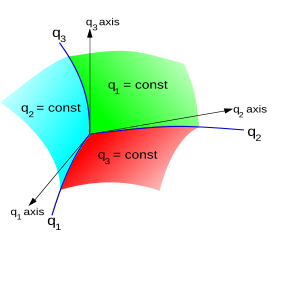
For now, consider 3-D space. A point P in 3-D space (or its position vector r) can be defined using Cartesian coordinates (x, y, z) , by ${\displaystyle \mathbf {r} =x\mathbf {e} _{x}+y\mathbf {e} _{y}+z\mathbf {e} _{z}}$, where e_x, e_y, e_z are the standard basis vectors.

It can also be defined by its curvilinear coordinates (q¹, q², q³) if this triplet of numbers defines a single point in an unambiguous way. The relation between the coordinates is then given by the invertible transformation functions:

${\displaystyle x=f^{1}(q^{1},q^{2},q^{3}),\,y=f^{2}(q^{1},q^{2},q^{3}),\,z=f^{3}(q^{1},q^{2},q^{3})}$

${\displaystyle q^{1}=g^{1}(x,y,z),\,q^{2}=g^{2}(x,y,z),\,q^{3}=g^{3}(x,y,z)}$

The surfaces q¹ = constant, q² = constant, q³ = constant are called the coordinate surfaces; and the space curves formed by their intersection in pairs are called the coordinate curves. The coordinate axes are determined by the tangents to the coordinate curves at the intersection of three surfaces. They are not in general fixed directions in space, which happens to be the case for simple Cartesian coordinates, and thus there is generally no natural global basis for curvilinear coordinates.

In the Cartesian system, the standard basis vectors can be derived from the derivative of the location of point P with respect to the local coordinate

${\displaystyle \mathbf {e} _{x}={\dfrac {\partial \mathbf {r} }{\partial x}};\;\mathbf {e} _{y}={\dfrac {\partial \mathbf {r} }{\partial y}};\;\mathbf {e} _{z}={\dfrac {\partial \mathbf {r} }{\partial z}}.}$

Applying the same derivatives to the curvilinear system locally at point P defines the natural basis vectors:

${\displaystyle \mathbf {h} _{1}={\dfrac {\partial \mathbf {r} }{\partial q^{1}}};\;\mathbf {h} _{2}={\dfrac {\partial \mathbf {r} }{\partial q^{2}}};\;\mathbf {h} _{3}={\dfrac {\partial \mathbf {r} }{\partial q^{3}}}.}$

Such a basis, whose vectors change their direction and/or magnitude from point to point is called a local basis. All bases associated with curvilinear coordinates are necessarily local. Basis vectors that are the same at all points are global bases, and can be associated only with linear or affine coordinate systems.

For this article e is reserved for the standard basis (Cartesian) and h or b is for the curvilinear basis.

These may not have unit length, and may also not be orthogonal. In the case that they are orthogonal at all points where the derivatives are well-defined, we define the Lamé coefficients (after Gabriel Lamé) by

${\displaystyle h_{1}=|\mathbf {h} _{1}|;\;h_{2}=|\mathbf {h} _{2}|;\;h_{3}=|\mathbf {h} _{3}|}$

and the curvilinear orthonormal basis vectors by

${\displaystyle {\mathbf{b}}_1={\displaystyle \frac{{\mathbf{h}}_1}{h_1}};{\mathbf{b}}_2={\displaystyle \frac{{\mathbf{h}}_2}{h_2}};{\mathbf{b}}_3={\displaystyle \frac{{}_{}}{}}}$Zdroj:https://en.wikipedia.org?pojem=Curvilinear_coordinates
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---