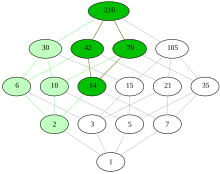
In the mathematical field of order theory, an ultrafilter on a given partially ordered set (or "poset") ${\textstyle P}$ is a certain subset of ${\displaystyle P,}$ namely a maximal filter on ${\displaystyle P;}$ that is, a proper filter on ${\textstyle P}$ that cannot be enlarged to a bigger proper filter on ${\displaystyle P.}$

If ${\displaystyle X}$ is an arbitrary set, its power set ${\displaystyle {\mathcal {P}}(X),}$ ordered by set inclusion, is always a Boolean algebra and hence a poset, and ultrafilters on ${\displaystyle {\mathcal {P}}(X)}$ are usually called ultrafilters on the set ${\displaystyle X}$.^{[note 1]} An ultrafilter on a set ${\displaystyle X}$ may be considered as a finitely additive 0-1-valued measure on ${\displaystyle {\mathcal {P}}(X)}$. In this view, every subset of ${\displaystyle X}$ is either considered "almost everything" (has measure 1) or "almost nothing" (has measure 0), depending on whether it belongs to the given ultrafilter or not.^[1]: §4

Ultrafilters have many applications in set theory, model theory, topology^[2]: 186 and combinatorics.^[3]

Ultrafilters on partial orders

In order theory, an ultrafilter is a subset of a partially ordered set that is maximal among all proper filters. This implies that any filter that properly contains an ultrafilter has to be equal to the whole poset.

Formally, if ${\textstyle P}$ is a set, partially ordered by ${\displaystyle \,\leq \,}$ then

• a subset ${\displaystyle F\subseteq P}$ is called a filter on ${\textstyle P}$ if
  • ${\displaystyle F}$ is nonempty,
  • for every ${\displaystyle x,y\in F,}$ there exists some element ${\displaystyle z\in F}$ such that ${\displaystyle z\leq x}$ and ${\displaystyle z\leq y,}$ and
  • for every ${\displaystyle x\in F}$ and ${\displaystyle y\in P,}$ ${\displaystyle x\leq y}$ implies that ${\displaystyle y}$ is in ${\displaystyle F}$ too;
• a proper subset ${\displaystyle U}$ of ${\textstyle P}$ is called an ultrafilter on ${\textstyle P}$ if
  • ${\displaystyle U}$ is a filter on ${\displaystyle P,}$ and
  • there is no proper filter ${\displaystyle F}$ on ${\textstyle P}$ that properly extends ${\displaystyle U}$ (that is, such that ${\displaystyle U}$ is a proper subset of ${\displaystyle F}$).

Types and existence of ultrafilters

Every ultrafilter falls into exactly one of two categories: principal or free. A principal (or fixed, or trivial) ultrafilter is a filter containing a least element. Consequently, each principal ultrafilter is of the form ${\displaystyle F_{p}=\{x:p\leq x\}}$ for some element ${\displaystyle p}$ of the given poset. In this case ${\displaystyle p}$ is called the principal element of the ultrafilter. Any ultrafilter that is not principal is called a free (or non-principal) ultrafilter. For arbitrary ${\displaystyle p}$, the set ${\displaystyle F_{p}}$ is a filter, called the principal filter at ${\displaystyle p}$; it is a principal ultrafilter only if it is maximal.

For ultrafilters on a powerset ${\displaystyle {\mathcal {P}}(X),}$ a principal ultrafilter consists of all subsets of ${\displaystyle X}$ that contain a given element ${\displaystyle x\in X.}$ Each ultrafilter on ${\displaystyle {\mathcal {P}}(X)}$ that is also a principal filter is of this form.^[2]: 187 Therefore, an ultrafilter ${\displaystyle U}$ on ${\displaystyle {\mathcal {P}}(X)}$ is principal if and only if it contains a finite set.^{[note 2]} If ${\displaystyle X}$ is infinite, an ultrafilter ${\displaystyle U}$ on ${\displaystyle {\mathcal {P}}(X)}$ is hence non-principal if and only if it contains the Fréchet filter of cofinite subsets of ${\displaystyle X.}$^{[note 3][4]: Proposition 3} If ${\displaystyle X}$ is finite, every ultrafilter is principal.^[2]: 187 If ${\displaystyle X}$ is infinite then the Fréchet filter is not an ultrafilter on the power set of ${\displaystyle X}$ but it is an ultrafilter on the finite–cofinite algebra of ${\displaystyle X.}$

Every filter on a Boolean algebra (or more generally, any subset with the finite intersection property) is contained in an ultrafilter (see ultrafilter lemma) and that free ultrafilters therefore exist, but the proofs involve the axiom of choice (AC) in the form of Zorn's lemma. On the other hand, the statement that every filter is contained in an ultrafilter does not imply AC. Indeed, it is equivalent to the Boolean prime ideal theorem (BPIT), a well-known intermediate point between the axioms of Zermelo–Fraenkel set theory (ZF) and the ZF theory augmented by the axiom of choice (ZFC). In general, proofs involving the axiom of choice do not produce explicit examples of free ultrafilters, though it is possible to find explicit examples in some models of ZFC; for example, Gödel showed that this can be done in the constructible universe where one can write down an explicit global choice function. In ZF without the axiom of choice, it is possible that every ultrafilter is principal.^[5]

Ultrafilter on a Boolean algebra

An important special case of the concept occurs if the considered poset is a Boolean algebra. In this case, ultrafilters are characterized by containing, for each element ${\displaystyle x}$ of the Boolean algebra, exactly one of the elements ${\displaystyle x}$ and ${\displaystyle \lnot x}$ (the latter being the Boolean complement of ${\displaystyle x}$):

If ${\textstyle P}$ is a Boolean algebra and ${\displaystyle F}$ is a proper filter on ${\displaystyle P,}$ then the following statements are equivalent:

1. ${\displaystyle F}$ is an ultrafilter on ${\displaystyle P,}$
2. ${\displaystyle F}$ is a prime filter on ${\displaystyle P,}$
3. for each ${\displaystyle x\in P,}$ either ${\displaystyle x\in F}$ or (${\displaystyle \lnot x}$) $$Zdroj:https://en.wikipedia.org?pojem=Ultrafilter
   Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

   ---