Spheroids with vertical rotational axes

oblate		prolate

A spheroid, also known as an ellipsoid of revolution or rotational ellipsoid, is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters. A spheroid has circular symmetry.

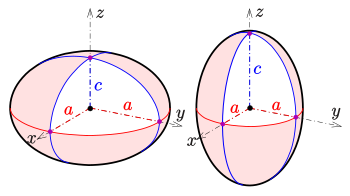
If the ellipse is rotated about its major axis, the result is a prolate spheroid, elongated like a rugby ball. The American football is similar but has a pointier end than a spheroid could. If the ellipse is rotated about its minor axis, the result is an oblate spheroid, flattened like a lentil or a plain M&M. If the generating ellipse is a circle, the result is a sphere.

Due to the combined effects of gravity and rotation, the figure of the Earth (and of all planets) is not quite a sphere, but instead is slightly flattened in the direction of its axis of rotation. For that reason, in cartography and geodesy the Earth is often approximated by an oblate spheroid, known as the reference ellipsoid, instead of a sphere. The current World Geodetic System model uses a spheroid whose radius is 6,378.137 km (3,963.191 mi) at the Equator and 6,356.752 km (3,949.903 mi) at the poles.

The word spheroid originally meant "an approximately spherical body", admitting irregularities even beyond the bi- or tri-axial ellipsoidal shape; that is how the term is used in some older papers on geodesy (for example, referring to truncated spherical harmonic expansions of the Earth's gravity geopotential model).^[1]

Equation

The equation of a tri-axial ellipsoid centred at the origin with semi-axes a, b and c aligned along the coordinate axes is

${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=1.}$

The equation of a spheroid with z as the symmetry axis is given by setting a = b:

${\displaystyle {\frac {x^{2}+y^{2}}{a^{2}}}+{\frac {z^{2}}{c^{2}}}=1.}$

The semi-axis a is the equatorial radius of the spheroid, and c is the distance from centre to pole along the symmetry axis. There are two possible cases:

• c < a: oblate spheroid
• c > a: prolate spheroid

The case of a = c reduces to a sphere.

Properties

Area

An oblate spheroid with c < a has surface area

${\displaystyle S_{\text{oblate}}=2\pi a^{2}\left(1+{\frac {1-e^{2}}{e}}\operatorname {arctanh} e\right)=2\pi a^{2}+\pi {\frac {c^{2}}{e}}\ln \left({\frac {1+e}{1-e}}\right)\qquad {\mbox{where}}\quad e^{2}=1-{\frac {c^{2}}{a^{2}}}.}$

The oblate spheroid is generated by rotation about the z-axis of an ellipse with semi-major axis a and semi-minor axis c, therefore e may be identified as the eccentricity. (See ellipse.)^[2]

A prolate spheroid with c > a has surface area

${\displaystyle S_{\text{prolate}}=2\pi a^{2}\left(1+{\frac {c}{ae}}\arcsin \,e\right)\qquad {\mbox{where}}\quad e^{2}=1-{\frac {a^{2}}{c^{2}}}.}$

The prolate spheroid is generated by rotation about the z-axis of an ellipse with semi-major axis c and semi-minor axis a; therefore, e may again be identified as the eccentricity. (See ellipse.) ^[3]

These formulas are identical in the sense that the formula for S_oblate can be used to calculate the surface area of a prolate spheroid and vice versa. However, e then becomes imaginary and can no longer directly be identified with the eccentricity. Both of these results may be cast into many other forms using standard mathematical identities and relations between parameters of the ellipse.

Volume

The volume inside a spheroid (of any kind) is

${\displaystyle {\tfrac {4}{3}}\pi a^{2}c\approx 4.19a^{2}c.}$

If A = 2a is the equatorial diameter, and C = 2c is the polar diameter, the volume is

${\displaystyle {\tfrac {\pi }{6}}A^{2}C\approx 0.523A^{2}C.}$

Curvature

Let a spheroid be parameterized as

${\displaystyle {\boldsymbol {\sigma }}(\beta ,\lambda )=(a\cos \beta \cos \lambda ,a\cos \beta \sin \lambda ,c\sin \beta ),}$

where β is the reduced latitude or parametric latitude, λ is the longitude, and −π/2 < β < +π/2 and −π < λ < +π. Then, the spheroid's Gaussian curvature is

${\displaystyle K(\beta ,\lambda )={\frac {c^{2}}{\left(a^{2}+\left(c^{2}-a^{2}\right)\cos ^{2}\beta \right)^{2}}},}$

and its mean curvature is

${\displaystyle H(\beta ,\lambda )={\frac {c\left(2a^{2}+\left(c^{2}-a^{2}\right)\cos ^{2}\beta \right)}{2a\left(a^{2}+\left(c^{2}-a^{2}\right)\cos ^{2}\beta \right)^{\frac {3}{2}}}}.}$

Both of these curvatures are always positive, so that every point on a spheroid is elliptic.

Aspect ratio

The aspect ratio of an oblate spheroid/ellipse, c : a, is the ratio of the polar to equatorial lengths, while the flattening (also called oblateness) f, is the ratio of the equatorial-polar length difference to the equatorial length:

${\displaystyle f={\frac {a-c}{a}}=1-{\frac {c}{a}}.}$

The first eccentricity (usually simply eccentricity, as above) is often used instead of flattening.^[4] It is defined by:

${\displaystyle e={\sqrt {1-{\frac {c^{2}}{a^{2}}}}}}$

The relations between eccentricity and flattening are:

Zdroj:https://en.wikipedia.org?pojem=Spheroid
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---