In classical mechanics, the shell theorem gives gravitational simplifications that can be applied to objects inside or outside a spherically symmetrical body. This theorem has particular application to astronomy.

Isaac Newton proved the shell theorem^[1] and stated that:

1. A spherically symmetric body affects external objects gravitationally as though all of its mass were concentrated at a point at its center.
2. If the body is a spherically symmetric shell (i.e., a hollow ball), no net gravitational force is exerted by the shell on any object inside, regardless of the object's location within the shell.

A corollary is that inside a solid sphere of constant density, the gravitational force within the object varies linearly with distance from the center, becoming zero by symmetry at the center of mass. This can be seen as follows: take a point within such a sphere, at a distance ${\displaystyle r}$ from the center of the sphere. Then you can ignore all of the shells of greater radius, according to the shell theorem (2). But the point can be considered to be external to the remaining sphere of radius r, and according to (1) all of the mass of this sphere can be considered to be concentrated at its centre. The remaining mass ${\displaystyle m}$ is proportional to ${\displaystyle r^{3}}$ (because it is based on volume). The gravitational force exerted on a body at radius r will be proportional to ${\displaystyle m/r^{2}}$ (the inverse square law), so the overall gravitational effect is proportional to ${\displaystyle r^{3}/r^{2}=r}$, so is linear in ${\displaystyle r}$.

These results were important to Newton's analysis of planetary motion; they are not immediately obvious, but they can be proven with calculus. (Gauss's law for gravity offers an alternative way to state the theorem.)

In addition to gravity, the shell theorem can also be used to describe the electric field generated by a static spherically symmetric charge density, or similarly for any other phenomenon that follows an inverse square law. The derivations below focus on gravity, but the results can easily be generalized to the electrostatic force.

Derivation of gravitational field outside of a solid sphere

There are three steps to proving Newton's shell theorem (1). First, the equation for a gravitational field due to a ring of mass will be derived. Arranging an infinite number of infinitely thin rings to make a disc, this equation involving a ring will be used to find the gravitational field due to a disk. Finally, arranging an infinite number of infinitely thin discs to make a sphere, this equation involving a disc will be used to find the gravitational field due to a sphere.

The gravitational field ${\displaystyle E}$ at a position called ${\displaystyle P}$ at ${\displaystyle (x,y)=(-p,0)}$ on the x-axis due to a point of mass ${\displaystyle M}$ at the origin is

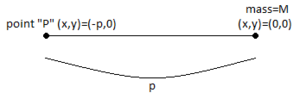Suppose that this mass is moved upwards along the y-axis to the point ${\displaystyle (-p,R)}$. The distance between ${\displaystyle P}$ and the point mass is now longer than before; It becomes the hypotenuse of the right triangle with legs ${\displaystyle p}$ and ${\displaystyle R}$ which is ${\textstyle {\sqrt {p^{2}+R^{2}}}}$. Hence, the gravitational field of the elevated point is:

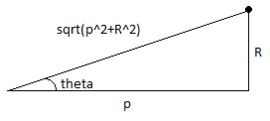
The magnitude of the gravitational field that would pull a particle at point ${\displaystyle P}$ in the x-direction is the gravitational field multiplied by ${\displaystyle \cos(\theta )}$ where ${\displaystyle \theta }$ is the angle adjacent to the x-axis. In this case, ${\displaystyle \cos(\theta )={\frac {p}{\sqrt {p^{2}+R^{2}}}}}$. Hence, the magnitude of the gravitational field in the x-direction, ${\displaystyle E_{x}}$ is:

Substituting in ${\displaystyle \cos(\theta )}$ gives Suppose that this mass is evenly distributed in a ring centered at the origin and facing point ${\displaystyle P}$ with the same radius ${\displaystyle R}$. Because all of the mass is located at the same angle with respect to the x-axis, and the distance between the points on the ring is the same distance as before, the gravitational field in the x-direction at point ${\displaystyle P}$ due to the ring is the same as a point mass located at a point ${\displaystyle R}$ units above the y-axis:

To find the gravitational field at point ${\displaystyle P}$ due to a disc, an infinite number of infinitely thin rings facing ${\displaystyle P}$, each with a radius ${\displaystyle y}$, width of ${\displaystyle dy}$, and mass of ${\displaystyle dM}$ may be placed inside one another to form a disc. The mass of any one of the rings ${\displaystyle dM}$ is the mass of the disc multiplied by the ratio of the area of the ring ${\displaystyle 2\pi y\,dy}$ to the total area of the disc ${\displaystyle \pi R^{2}}$. So, ${\textstyle dM={\frac {M\cdot 2y\,dy}{R^{2}}}}$. Hence, a small change in the gravitational field, ${\displaystyle E}$ is:

Substituting in ${\displaystyle dM}$ and integrating both sides gives the gravitational field of the disk: