Intersection

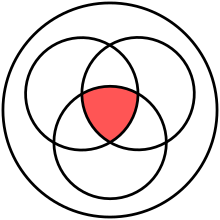
The intersection of two sets ${\displaystyle A}$ and ${\displaystyle B,}$ represented by circles. ${\displaystyle A\cap B}$ is in red.
Type	Set operation
Field	Set theory
Statement	The intersection of ${\displaystyle A}$ and ${\displaystyle B}$ is the set ${\displaystyle A\cap B}$ of elements that lie in both set ${\displaystyle A}$ and set ${\displaystyle B}$.
Symbolic statement	${\displaystyle A\cap B=\{x:x\in A{\text{ and }}x\in B\}}$

In set theory, the intersection of two sets ${\displaystyle A}$ and ${\displaystyle B,}$ denoted by ${\displaystyle A\cap B,}$^[1] is the set containing all elements of ${\displaystyle A}$ that also belong to ${\displaystyle B}$ or equivalently, all elements of ${\displaystyle B}$ that also belong to ${\displaystyle A.}$^[2]

Notation and terminology

Intersection is written using the symbol "${\displaystyle \cap }$" between the terms; that is, in infix notation. For example:

$${\displaystyle \{1,2,3\}\cap \{2,3,4\}=\{2,3\}}$$

$${\displaystyle \{1,2,3\}\cap \{4,5,6\}=\varnothing }$$

$${\displaystyle \mathbb {Z} \cap \mathbb {N} =\mathbb {N} }$$

$${\displaystyle \{x\in \mathbb {R} :x^{2}=1\}\cap \mathbb {N} =\{1\}}$$

$${\displaystyle \bigcap _{i=1}^{n}A_{i}}$$

For an explanation of the symbols used in this article, refer to the table of mathematical symbols.

Definition

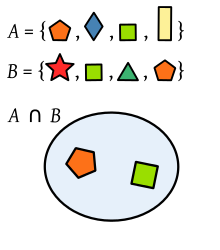
The intersection of two sets ${\displaystyle A}$ and ${\displaystyle B,}$ denoted by ${\displaystyle A\cap B}$,^[3] is the set of all objects that are members of both the sets ${\displaystyle A}$ and ${\displaystyle B.}$ In symbols:

$${\displaystyle A\cap B=\{x:x\in A{\text{ and }}x\in B\}.}$$

That is, ${\displaystyle x}$ is an element of the intersection ${\displaystyle A\cap B}$ if and only if ${\displaystyle x}$ is both an element of ${\displaystyle A}$ and an element of ${\displaystyle B.}$^[3]

For example:

• The intersection of the sets {1, 2, 3} and {2, 3, 4} is {2, 3}.
• The number 9 is not in the intersection of the set of prime numbers {2, 3, 5, 7, 11, ...} and the set of odd numbers {1, 3, 5, 7, 9, 11, ...}, because 9 is not prime.

Intersecting and disjoint sets

We say that ${\displaystyle A}$ intersects (meets) ${\displaystyle B}$ if there exists some ${\displaystyle x}$ that is an element of both ${\displaystyle A}$ and ${\displaystyle B,}$ in which case we also say that ${\displaystyle A}$ intersects (meets) ${\displaystyle B}$ at ${\displaystyle x}$. Equivalently, ${\displaystyle A}$ intersects ${\displaystyle B}$ if their intersection ${\displaystyle A\cap B}$ is an inhabited set, meaning that there exists some ${\displaystyle x}$ such that ${\displaystyle x\in A\cap B.}$

We say that ${\displaystyle A}$ and ${\displaystyle B}$ are disjoint if ${\displaystyle A}$ does not intersect ${\displaystyle B.}$ In plain language, they have no elements in common. ${\displaystyle A}$ and ${\displaystyle B}$ are disjoint if their intersection is empty, denoted ${\displaystyle A\cap B=\varnothing .}$

For example, the sets ${\displaystyle \{1,2\}}$ and ${\displaystyle \{3,4\}}$ are disjoint, while the set of even numbers intersects the set of multiples of 3 at the multiples of 6.

Algebraic properties

Binary intersection is an associative operation; that is, for any sets ${\displaystyle A,B,}$ and ${\displaystyle C,}$ one has