In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module Q that shares certain desirable properties with the Z-module Q of all rational numbers. Specifically, if Q is a submodule of some other module, then it is already a direct summand of that module; also, given a submodule of a module Y, any module homomorphism from this submodule to Q can be extended to a homomorphism from all of Y to Q. This concept is dual to that of projective modules. Injective modules were introduced in (Baer 1940) and are discussed in some detail in the textbook (Lam 1999, §3).

Injective modules have been heavily studied, and a variety of additional notions are defined in terms of them: Injective cogenerators are injective modules that faithfully represent the entire category of modules. Injective resolutions measure how far from injective a module is in terms of the injective dimension and represent modules in the derived category. Injective hulls are maximal essential extensions, and turn out to be minimal injective extensions. Over a Noetherian ring, every injective module is uniquely a direct sum of indecomposable modules, and their structure is well understood. An injective module over one ring, may not be injective over another, but there are well-understood methods of changing rings which handle special cases. Rings which are themselves injective modules have a number of interesting properties and include rings such as group rings of finite groups over fields. Injective modules include divisible groups and are generalized by the notion of injective objects in category theory.

Definition

A left module Q over the ring R is injective if it satisfies one (and therefore all) of the following equivalent conditions:

• If Q is a submodule of some other left R-module M, then there exists another submodule K of M such that M is the internal direct sum of Q and K, i.e. Q + K = M and Q ∩ K = {0}.
• Any short exact sequence 0 →Q → M → K → 0 of left R-modules splits.
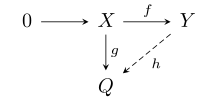
• If X and Y are left R-modules, f : X → Y is an injective module homomorphism and g : X → Q is an arbitrary module homomorphism, then there exists a module homomorphism h : Y → Q such that hf = g, i.e. such that the following diagram commutes:

• The contravariant Hom functor Hom(-,Q) from the category of left R-modules to the category of abelian groups is exact.

Injective right R-modules are defined in complete analogy.

Examples

First examples

Trivially, the zero module {0} is injective.

Given a field k, every k-vector space Q is an injective k-module. Reason: if Q is a subspace of V, we can find a basis of Q and extend it to a basis of V. The new extending basis vectors span a subspace K of V and V is the internal direct sum of Q and K. Note that the direct complement K of Q is not uniquely determined by Q, and likewise the extending map h in the above definition is typically not unique.

The rationals Q (with addition) form an injective abelian group (i.e. an injective Z-module). The factor group Q/Z and the circle group are also injective Z-modules. The factor group Z/nZ for n > 1 is injective as a Z/nZ-module, but not injective as an abelian group.

Commutative examples

More generally, for any integral domain R with field of fractions K, the R-module K is an injective R-module, and indeed the smallest injective R-module containing R. For any Dedekind domain, the quotient module K/R is also injective, and its indecomposable summands are the localizations ${\displaystyle R_{\mathfrak {p}}/R}$ for the nonzero prime ideals ${\displaystyle {\mathfrak {p}}}$. The zero ideal is also prime and corresponds to the injective K. In this way there is a 1-1 correspondence between prime ideals and indecomposable injective modules.

A particularly rich theory is available for commutative noetherian rings due to Eben Matlis, (Lam 1999, §3I). Every injective module is uniquely a direct sum of indecomposable injective modules, and the indecomposable injective modules are uniquely identified as the injective hulls of the quotients R/P where P varies over the prime spectrum of the ring. The injective hull of R/P as an R-module is canonically an R_P module, and is the R_P-injective hull of R/P. In other words, it suffices to consider local rings. The endomorphism ring of the injective hull of R/P is the completion ${\displaystyle {\hat {R}}_{P}}$ of R at P.^[1]

Two examples are the injective hull of the Z-module Z/pZ (the Prüfer group), and the injective hull of the k-module k (the ring of inverse polynomials). The latter is easily described as k/xk. This module has a basis consisting of "inverse monomials", that is x⁻ⁿ for n = 0, 1, 2, …. Multiplication by scalars is as expected, and multiplication by x behaves normally except that x·1 = 0. The endomorphism ring is simply the ring of formal power series.

Artinian examples

If G is a finite group and k a field with characteristic 0, then one shows in the theory of group representations that any subrepresentation of a given one is already a direct summand of the given one. Translated into module language, this means that all modules over the group algebra kG are injective. If the characteristic of k is not zero, the following example may help.

If A is a unital associative algebra over the field k with finite dimension over k, then Hom_k(−, k) is a duality between finitely generated left A-modules and finitely generated right A-modules. Therefore, the finitely generated injective left A-modules are precisely the modules of the form Hom_k(P, k) where P is a finitely generated projective right A-module. For symmetric algebras, the duality is particularly well-behaved and projective modules and injective modules coincide.

For any Artinian ring, just as for commutative rings, there is a 1-1 correspondence between prime ideals and indecomposable injective modules. The correspondence in this case is perhaps even simpler: a prime ideal is an annihilator of a unique simple module, and the corresponding indecomposable injective module is its injective hull. For finite-dimensional algebras over fields, these injective hulls are finitely-generated modules (Lam 1999, §3G, §3J).

Computing injective hulls

If ${\displaystyle R}$ is a Noetherian ring and ${\displaystyle {\mathfrak {p}}}$ is a prime ideal, set ${\displaystyle E=E(R/{\mathfrak {p}})}$ as the injective hull. The injective hull of ${\displaystyle R/{\mathfrak {p}}}$ over the Artinian ring ${\displaystyle R/{\mathfrak {p}}^{k}}$ can be computed as the module ${\displaystyle (0:_{E}{\mathfrak {p}}^{k})}$. It is a module of the same length as ${\displaystyle R/{\mathfrak {p}}^{k}}$.^[2] In particular, for the standard graded ring ${\displaystyle R_{\bullet }=k_{\bullet }}$ and ${\displaystyle {\mathfrak {p}}=(x_{1},\ldots ,x_{n})}$, ${\displaystyle E=\oplus _{i}{\text{Hom}}(R_{i},k)}$ is an injective module, giving the tools for computing the indecomposable injective modules for artinian rings over ${\displaystyle k}$.

Self-injectivity

An Artin local ring ${\displaystyle (R,{\mathfrak {m}},K)}$ is injective over itself if and only if ${\displaystyle soc(R)}$ is a 1-dimensional vector space over ${\displaystyle K}$. This implies every local Gorenstein ring which is also Artin is injective over itself since has a 1-dimensional socle.^[3] A simple non-example is the ring ${\displaystyle R=\mathbb {C} /(x^{2},xy,y^{2})}$ which has maximal ideal ${\displaystyle (x,y)}$ and residue field ${\displaystyle \mathbb {C} }$. Its socle is ${\displaystyle \mathbb {C} \cdot x\oplus \mathbb {C} \cdot y}$, which is 2-dimensional. The residue field has the injective hull ${\displaystyle {\text{Hom}}_{\mathbb {C} }(\mathbb {C} \cdot x\oplus \mathbb {C} \cdot y,\mathbb {C} )}$.

Modules over Lie algebras

For a Lie algebra ${\displaystyle {\mathfrak {g}}}$ over a field ${\displaystyle k}$ of characteristic 0, the category of modules ${\displaystyle {\mathcal {M}}({\mathfrak {g}})}$ has a relatively straightforward description of its injective modules.^[4] Using the universal enveloping algebra any injective ${\displaystyle \mathfrak{g}}$Zdroj:https://en.wikipedia.org?pojem=Self-injective_ring
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.