This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Rotation" – news · newspapers · books · scholar · JSTOR (March 2014) (Learn how and when to remove this template message)

Rotation or rotational motion is the circular movement of an object around a central line, known as axis of rotation. A plane figure can rotate in either a clockwise or counterclockwise sense around a perpendicular axis intersecting anywhere inside or outside the figure at a center of rotation. A solid figure has an infinite number of possible axes and angles of rotation, including chaotic rotation (between arbitrary orientations), in contrast to rotation around a fixed axis.

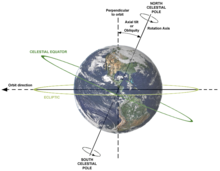
The special case of a rotation with an internal axis passing through the body's own center of mass is known as a spin (or autorotation).^[1] In that case, the surface intersection of the internal spin axis can be called a pole; for example, Earth's rotation defines the geographical poles. A rotation around an axis completely external to the moving body is called a revolution (or orbit), e.g. Earth's orbit around the Sun. The ends of the external axis of revolution can be called the orbital poles.^[1]

Either type of rotation is involved in a corresponding type of angular velocity (spin angular velocity and orbital angular velocity) and angular momentum (spin angular momentum and orbital angular momentum).

Mathematics

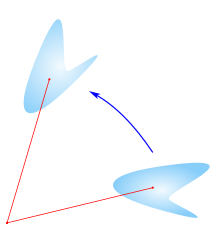
Mathematically, a rotation is a rigid body movement which, unlike a translation, keeps at least one point fixed. This definition applies to rotations in two dimensions (in a plane), in which exactly one point is kept fixed; and also in three dimensions (in space), in which additional points may be kept fixed (as in rotation around a fixed axis, as infinite line).

All rigid body movements are rotations, translations, or combinations of the two.

A rotation is simply a progressive radial orientation to a common point. That common point lies within the axis of that motion. The axis is perpendicular to the plane of the motion.

If a rotation around a point or axis is followed by a second rotation around the same point/axis, a third rotation results. The reverse (inverse) of a rotation is also a rotation. Thus, the rotations around a point/axis form a group. However, a rotation around a point or axis and a rotation around a different point/axis may result in something other than a rotation, e.g. a translation.

Rotations around the x, y and z axes are called principal rotations. Rotation around any axis can be performed by taking a rotation around the x axis, followed by a rotation around the y axis, and followed by a rotation around the z axis. That is to say, any spatial rotation can be decomposed into a combination of principal rotations.

Fixed axis vs. fixed point

The combination of any sequence of rotations of an object in three dimensions about a fixed point is always equivalent to a rotation about an axis (which may be considered to be a rotation in the plane that is perpendicular to that axis). Similarly, the rotation rate of an object in three dimensions at any instant is about some axis, although this axis may be changing over time.

In other than three dimensions, it does not make sense to describe a rotation as being around an axis, since more than one axis through the object may be kept fixed; instead, simple rotations are described as being in a plane. In four or more dimensions, a combination of two or more rotations about in a plane is not in general a rotation in a single plane.

Axis of 2-dimensional rotations

2-dimensional rotations, unlike the 3-dimensional ones, possess no axis of rotation, only a point about which the rotation occurs. This is equivalent, for linear transformations, with saying that there is no direction in the plane which is kept unchanged by a 2 dimensional rotation, except, of course, the identity.

The question of the existence of such a direction is the question of existence of an eigenvector for the matrix A representing the rotation. Every 2D rotation around the origin through an angle ${\displaystyle \theta }$ in counterclockwise direction can be quite simply represented by the following matrix:

${\displaystyle A={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}}}$

A standard eigenvalue determination leads to the characteristic equation

${\displaystyle \lambda ^{2}-2\lambda \cos \theta +1=0,}$

which has

${\displaystyle \cos \theta \pm i\sin \theta }$

as its eigenvalues. Therefore, there is no real eigenvalue whenever ${\displaystyle \cos \theta \neq \pm 1}$, meaning that no real vector in the plane is kept unchanged by A.

Rotation angle and axis in 3 dimensions

Knowing that the trace is an invariant, the rotation angle ${\displaystyle \alpha }$ for a proper orthogonal 3×3 rotation matrix ${\displaystyle A}$ is found by

${\displaystyle \alpha =\cos ^{-1}\left({\frac {A_{11}+A_{22}+A_{33}-1}{2}}\right)}$

Using the principal arc-cosine, this formula gives a rotation angle satisfying ${\displaystyle 0\leq \alpha \leq 180^{\circ }}$. The corresponding rotation axis must be defined to point in a direction that limits the rotation angle to not exceed 180 degrees. (This can always be done because any rotation of more than 180 degrees about an axis ${\displaystyle m}$ can always be written as a rotation having ${\displaystyle 0\leq \alpha \leq 180^{\circ }}$ if the axis is replaced with ${\displaystyle n=-m}$.)

Every proper rotation ${\displaystyle A}$ in 3D space has an axis of rotation, which is defined such that any vector ${\displaystyle v}$ that is aligned with the rotation axis will not be affected by rotation. Accordingly, ${\displaystyle Av=v}$, and the rotation axis therefore corresponds to an eigenvector of the rotation matrix associated with an eigenvalue of 1. As long as the rotation angle ${\displaystyle \alpha }$ is nonzero (i.e., the rotation is not the identity tensor), there is one and only one such direction. Because A has only real components, there is at least one real eigenvalue, and the remaining two eigenvalues must be complex conjugates of each other (see Eigenvalues and eigenvectors#Eigenvalues and the characteristic polynomial). Knowing that 1 is an eigenvalue, it follows that the remaining two eigenvalues are complex conjugates of each other, but this does not imply that they are complex—they could be real with double multiplicity. In the degenerate case of a rotation angle ${\displaystyle \alpha =180^{\circ }}$, the remaining two eigenvalues are both equal to −1. In the degenerate case of a zero rotation angle, the rotation matrix is the identity, and all three eigenvalues are 1 (which is the only case for which the rotation axis is arbitrary).

A spectral analysis is not required to find the rotation axis. If ${\displaystyle n}$ denotes the unit eigenvector aligned with the rotation axis, and if ${\displaystyle \alpha }$ denotes the rotation angle, then it can be shown that ${\displaystyle 2\sin(\alpha )n=\{A_{32}-A_{23},A_{13}-A_{31},A_{21}-A_{12}\}}$. Consequently, the expense of an eigenvalue analysis can be avoided by simply normalizing this vector if it has a nonzero magnitude. On the other hand, if this vector has a zero magnitude, it means that ${\displaystyle \sin(\alpha )=0}$. In other words, this vector will be zero if and only if the rotation angle is 0 or 180 degrees, and the rotation axis may be assigned in this case by normalizing any column of ${\displaystyle A+I}$ that has a nonzero magnitude.^[2]

This discussion applies to a proper rotation, and hence ${\displaystyle \det A=1}$. Any improper orthogonal 3x3 matrix ${\displaystyle B}$ may be written as ${\displaystyle B=-A}$, in which ${\displaystyle A}$ is proper orthogonal. That is, any improper orthogonal 3x3 matrix may be decomposed as a proper rotation (from which an axis of rotation can be found as described above) followed by an inversion (multiplication by −1). It follows that the rotation axis of ${\displaystyle A}$ is also the eigenvector of ${\displaystyle B}$ corresponding to an eigenvalue of −1.

Rotation plane

As much as every tridimensional rotation has a rotation axis, also every tridimensional rotation has a plane, which is perpendicular to the rotation axis, and which is left invariant by the rotation. The rotation, restricted to this plane, is an ordinary 2D rotation.

The proof proceeds similarly to the above discussion. First, suppose that all eigenvalues of the 3D rotation matrix A are real. This means that there is an orthogonal basis, made by the corresponding eigenvectors (which are necessarily orthogonal), over which the effect of the rotation matrix is just stretching it. If we write A in this basis, it is diagonal; but a diagonal orthogonal matrix is made of just +1s and −1s in the diagonal entries. Therefore, we do not have a proper rotation, but either the identity or the result of a sequence of reflections.

It follows, then, that a proper rotation has some complex eigenvalue. Let v be the corresponding eigenvector. Then, as we showed in the previous topic, ${\displaystyle {\bar {v}}}$ is also an eigenvector, and ${\displaystyle v+{\bar {v}}}$ and ${\displaystyle i(v-{\bar {v}})}$ are such that their scalar product vanishes:

${\displaystyle i(v^{\text{T}}+{\bar {v}}^{\text{T}})(v-{\bar {v}})=i(v^{\text{T}}v-{\bar {v}}^{\text{T}}{\bar {v}}+{\bar {v}}^{\text{T}}v-v^{\text{T}}{\bar {v}})=0}$Zdroj:https://en.wikipedia.org?pojem=Rotation
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---