This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (January 2021) This article is written like a research paper or scientific journal. Please help improve the article by rewriting it in encyclopedic style and simplify overly technical phrases. (January 2023) (Learn how and when to remove this template message) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Resonance" – news · newspapers · books · scholar · JSTOR (January 2021) (Learn how and when to remove this template message) ... (Learn how and when to remove this template message)

Resonance is the phenomenon, pertaining to oscillatory dynamical systems, wherein amplitude rises are caused by an external force with time-varying amplitude with the same frequency of variation as the natural frequency of the system.^[3] The amplitude rises that occur are a result of the fact that applied external forces at the natural frequency entail a net increase in mechanical energy of the system.

Resonance can occur in various systems, such as mechanical, electrical, or acoustic systems, and it is often desirable in certain applications, such as musical instruments or radio receivers. However, resonance can also be detrimental, leading to excessive vibrations or even structural failure in some cases.

All systems, including molecular systems and particles, tend to vibrate at a natural frequency depending upon their structure; this frequency is known as a resonant frequency or resonance frequency. When an oscillating force, an external vibration, is applied at a resonant frequency of a dynamic system, object, or particle, the outside vibration will cause the system to oscillate at a higher amplitude (with more force) than when the same force is applied at other, non-resonant frequencies.^[4]

The resonant frequencies of a system can be identified when the response to an external vibration creates an amplitude that is a relative maximum within the system.^[4] Small periodic forces that are near a resonant frequency of the system have the ability to produce large amplitude oscillations in the system due to the storage of vibrational energy.

Resonance phenomena occur with all types of vibrations or waves: there is mechanical resonance, orbital resonance, acoustic resonance, electromagnetic resonance, nuclear magnetic resonance (NMR), electron spin resonance (ESR) and resonance of quantum wave functions. Resonant systems can be used to generate vibrations of a specific frequency (e.g., musical instruments), or pick out specific frequencies from a complex vibration containing many frequencies (e.g., filters).

The term resonance (from Latin resonantia, 'echo', from resonare, 'resound') originated from the field of acoustics, particularly the sympathetic resonance observed in musical instruments, e.g., when one string starts to vibrate and produce sound after a different one is struck.

Overview

Resonance occurs when a system is able to store and easily transfer energy between two or more different storage modes (such as kinetic energy and potential energy in the case of a simple pendulum). However, there are some losses from cycle to cycle, called damping. When damping is small, the resonant frequency is approximately equal to the natural frequency of the system, which is a frequency of unforced vibrations. Some systems have multiple, distinct, resonant frequencies.

Examples

This section possibly contains original research. Please improve it by verifying the claims made and adding inline citations. Statements consisting only of original research should be removed. (February 2024) (Learn how and when to remove this template message)

A familiar example is a playground swing, which acts as a pendulum. Pushing a person in a swing in time with the natural interval of the swing (its resonant frequency) makes the swing go higher and higher (maximum amplitude), while attempts to push the swing at a faster or slower tempo produce smaller arcs. This is because the energy the swing absorbs is maximized when the pushes match the swing's natural oscillations.^{[citation needed]}

Resonance occurs widely in nature, and is exploited in many devices. It is the mechanism by which virtually all sinusoidal waves and vibrations are generated. For example, when hard objects like metal, glass, or wood are struck, there are brief resonant vibrations in the object.^{[citation needed]} Light and other short wavelength electromagnetic radiation is produced by resonance on an atomic scale, such as electrons in atoms. Other examples of resonance include:

• Timekeeping mechanisms of modern clocks and watches, e.g., the balance wheel in a mechanical watch and the quartz crystal in a quartz watch
• Tidal resonance of the Bay of Fundy
• Acoustic resonances of musical instruments and the human vocal tract
• Shattering of a crystal wineglass when exposed to a musical tone of the right pitch (its resonant frequency)
• Friction idiophones, such as making a glass object (glass, bottle, vase) vibrate by rubbing around its rim with a fingertip
• Electrical resonance of tuned circuits in radios and TVs that allow radio frequencies to be selectively received
• Creation of coherent light by optical resonance in a laser cavity
• Orbital resonance as exemplified by some moons of the Solar System's gas giants
• Material resonances in atomic scale are the basis of several spectroscopic techniques that are used in condensed matter physics
  • Electron spin resonance
  • Mössbauer effect
  • Nuclear magnetic resonance

Linear systems

Resonance manifests itself in many linear and nonlinear systems as oscillations around an equilibrium point. When the system is driven by a sinusoidal external input, a measured output of the system may oscillate in response. The ratio of the amplitude of the output's steady-state oscillations to the input's oscillations is called the gain, and the gain can be a function of the frequency of the sinusoidal external input. Peaks in the gain at certain frequencies correspond to resonances, where the amplitude of the measured output's oscillations are disproportionately large.

Since many linear and nonlinear systems that oscillate are modeled as harmonic oscillators near their equilibria, this section begins with a derivation of the resonant frequency for a driven, damped harmonic oscillator. The section then uses an RLC circuit to illustrate connections between resonance and a system's transfer function, frequency response, poles, and zeroes. Building off the RLC circuit example, the section then generalizes these relationships for higher-order linear systems with multiple inputs and outputs.

The driven, damped harmonic oscillator

Consider a damped mass on a spring driven by a sinusoidal, externally applied force. Newton's second law takes the form

$${\displaystyle m{\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}=F_{0}\sin(\omega t)-kx-c{\frac {\mathrm {d} x}{\mathrm {d} t}},}$$

(1)

where m is the mass, x is the displacement of the mass from the equilibrium point, F₀ is the driving amplitude, ω is the driving angular frequency, k is the spring constant, and c is the viscous damping coefficient. This can be rewritten in the form

$${\displaystyle {\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}+2\zeta \omega _{0}{\frac {\mathrm {d} x}{\mathrm {d} t}}+\omega _{0}^{2}x={\frac {F_{0}}{m}}\sin(\omega t),}$$

(2)

where

• ${\textstyle \omega _{0}={\sqrt {k/m}}}$ is called the undamped angular frequency of the oscillator or the natural frequency,
• ${\displaystyle \zeta ={\frac {c}{2{\sqrt {mk}}}}}$ is called the damping ratio.

Many sources also refer to ω₀ as the resonant frequency. However, as shown below, when analyzing oscillations of the displacement x(t), the resonant frequency is close to but not the same as ω₀. In general the resonant frequency is close to but not necessarily the same as the natural frequency.^[5] The RLC circuit example in the next section gives examples of different resonant frequencies for the same system.

The general solution of Equation (2) is the sum of a transient solution that depends on initial conditions and a steady state solution that is independent of initial conditions and depends only on the driving amplitude F₀, driving frequency ω, undamped angular frequency ω₀, and the damping ratio ζ. The transient solution decays in a relatively short amount of time, so to study resonance it is sufficient to consider the steady state solution.

It is possible to write the steady-state solution for x(t) as a function proportional to the driving force with an induced phase change φ,

$${\displaystyle x(t)={\frac {F_{0}}{m{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}}\sin(\omega t+\varphi ),}$$

(3)

where ${\displaystyle \varphi =\arctan \left({\frac {2\omega \omega _{0}\zeta }{\omega ^{2}-\omega _{0}^{2}}}\right)+n\pi .}$

The phase value is usually taken to be between −180° and 0 so it represents a phase lag for both positive and negative values of the arctan argument.

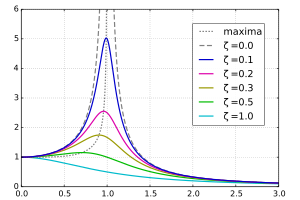
Resonance occurs when, at certain driving frequencies, the steady-state amplitude of x(t) is large compared to its amplitude at other driving frequencies. For the mass on a spring, resonance corresponds physically to the mass's oscillations having large displacements from the spring's equilibrium position at certain driving frequencies. Looking at the amplitude of x(t) as a function of the driving frequency ω, the amplitude is maximal at the driving frequency

$${\displaystyle \omega _{r}=\omega _{0}{\sqrt {1-2\zeta ^{2}}}.}$$

ω_r is the resonant frequency for this system. Again, the resonant frequency does not equal the undamped angular frequency ω₀ of the oscillator. They are proportional, and if the damping ratio goes to zero they are the same, but for non-zero damping they are not the same frequency. As shown in the figure, resonance may also occur at other frequencies near the resonant frequency, including ω₀, but the maximum response is at the resonant frequency.

Also, ω_r is only real and non-zero if ${\textstyle \zeta <1/{\sqrt {2}}}$, so this system can only resonate when the harmonic oscillator is significantly underdamped. For systems with a very small damping ratio and a driving frequency near the resonant frequency, the steady state oscillations can become very large.

The pendulum

For other driven, damped harmonic oscillators whose equations of motion do not look exactly like the mass on a spring example, the resonant frequency remains