In geometry, a polygon (/ˈpɒlɪɡɒn/) is a plane figure made up of line segments connected to form a closed polygonal chain.

The segments of a closed polygonal chain are called its edges or sides. The points where two edges meet are the polygon's vertices or corners. An n-gon is a polygon with n sides; for example, a triangle is a 3-gon.

A simple polygon is one which does not intersect itself. More precisely, the only allowed intersections among the line segments that make up the polygon are the shared endpoints of consecutive segments in the polygonal chain. A simple polygon is the boundary of a region of the plane that is called a solid polygon. The interior of a solid polygon is its body, also known as a polygonal region or polygonal area. In contexts where one is concerned only with simple and solid polygons, a polygon may refer only to a simple polygon or to a solid polygon.

A polygonal chain may cross over itself, creating star polygons and other self-intersecting polygons. Some sources also consider closed polygonal chains in Euclidean space to be a type of polygon (a skew polygon), even when the chain does not lie in a single plane.

A polygon is a 2-dimensional example of the more general polytope in any number of dimensions. There are many more generalizations of polygons defined for different purposes.

Etymology

The word polygon derives from the Greek adjective πολύς (polús) 'much', 'many' and γωνία (gōnía) 'corner' or 'angle'. It has been suggested that γόνυ (gónu) 'knee' may be the origin of gon.^[1]

Classification

Number of sides

Polygons are primarily classified by the number of sides.

Convexity and intersection

Polygons may be characterized by their convexity or type of non-convexity:

• Convex: any line drawn through the polygon (and not tangent to an edge or corner) meets its boundary exactly twice. As a consequence, all its interior angles are less than 180°. Equivalently, any line segment with endpoints on the boundary passes through only interior points between its endpoints. This condition is true for polygons in any geometry, not just Euclidean.^[2]
• Non-convex: a line may be found which meets its boundary more than twice. Equivalently, there exists a line segment between two boundary points that passes outside the polygon.
• Simple: the boundary of the polygon does not cross itself. All convex polygons are simple.
• Concave: Non-convex and simple. There is at least one interior angle greater than 180°.
• Star-shaped: the whole interior is visible from at least one point, without crossing any edge. The polygon must be simple, and may be convex or concave. All convex polygons are star-shaped.
• Self-intersecting: the boundary of the polygon crosses itself. The term complex is sometimes used in contrast to simple, but this usage risks confusion with the idea of a complex polygon as one which exists in the complex Hilbert plane consisting of two complex dimensions.
• Star polygon: a polygon which self-intersects in a regular way. A polygon cannot be both a star and star-shaped.

Equality and symmetry

• Equiangular: all corner angles are equal.
• Equilateral: all edges are of the same length.
• Regular: both equilateral and equiangular.
• Cyclic: all corners lie on a single circle, called the circumcircle.
• Tangential: all sides are tangent to an inscribed circle.
• Isogonal or vertex-transitive: all corners lie within the same symmetry orbit. The polygon is also cyclic and equiangular.
• Isotoxal or edge-transitive: all sides lie within the same symmetry orbit. The polygon is also equilateral and tangential.

The property of regularity may be defined in other ways: a polygon is regular if and only if it is both isogonal and isotoxal, or equivalently it is both cyclic and equilateral. A non-convex regular polygon is called a regular star polygon.

Miscellaneous

• Rectilinear: the polygon's sides meet at right angles, i.e. all its interior angles are 90 or 270 degrees.
• Monotone with respect to a given line L: every line orthogonal to L intersects the polygon not more than twice.

Properties and formulas

Euclidean geometry is assumed throughout.

Angles

Any polygon has as many corners as it has sides. Each corner has several angles. The two most important ones are:

• Interior angle – The sum of the interior angles of a simple n-gon is (n − 2) × π radians or (n − 2) × 180 degrees. This is because any simple n-gon ( having n sides ) can be considered to be made up of (n − 2) triangles, each of which has an angle sum of π radians or 180 degrees. The measure of any interior angle of a convex regular n-gon is ${\displaystyle \left(1-{\tfrac {2}{n}}\right)\pi }$ radians or ${\displaystyle 180-{\tfrac {360}{n}}}$ degrees. The interior angles of regular star polygons were first studied by Poinsot, in the same paper in which he describes the four regular star polyhedra: for a regular ${\displaystyle {\tfrac {p}{q}}}$-gon (a p-gon with central density q), each interior angle is ${\displaystyle {\tfrac {\pi (p-2q)}{p}}}$ radians or ${\displaystyle {\tfrac {180(p-2q)}{p}}}$ degrees.^[3]
• Exterior angle – The exterior angle is the supplementary angle to the interior angle. Tracing around a convex n-gon, the angle "turned" at a corner is the exterior or external angle. Tracing all the way around the polygon makes one full turn, so the sum of the exterior angles must be 360°. This argument can be generalized to concave simple polygons, if external angles that turn in the opposite direction are subtracted from the total turned. Tracing around an n-gon in general, the sum of the exterior angles (the total amount one rotates at the vertices) can be any integer multiple d of 360°, e.g. 720° for a pentagram and 0° for an angular "eight" or antiparallelogram, where d is the density or turning number of the polygon.

Area

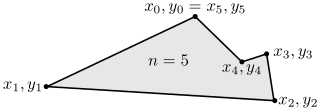
In this section, the vertices of the polygon under consideration are taken to be ${\displaystyle (x_{0},y_{0}),(x_{1},y_{1}),\ldots ,(x_{n-1},y_{n-1})}$ in order. For convenience in some formulas, the notation (x_n, y_n) = (x₀, y₀) will also be used.

Simple polygons

If the polygon is non-self-intersecting (that is, simple), the signed area is

${\displaystyle A={\frac {1}{2}}\sum _{i=0}^{n-1}(x_{i}y_{i+1}-x_{i+1}y_{i})\quad {\text{where }}x_{n}=x_{0}{\text{ and }}y_{n}=y_{0},}$

or, using determinants

${\displaystyle 16A^{2}=\sum _{i=0}^{n-1}\sum _{j=0}^{n-1}{\begin{vmatrix}Q_{i,j}&Q_{i,j+1}\\Q_{i+1,j}&Q_{i+1,j+1}\end{vmatrix}},}$

where ${\displaystyle Q_{i,j}}$ is the squared distance between ${\displaystyle (x_{i},y_{i})}$ and ${\displaystyle (x_{j},y_{j}).}$^[4][5]

The signed area depends on the ordering of the vertices and of the orientation of the plane. Commonly, the positive orientation is defined by the (counterclockwise) rotation that maps the positive x-axis to the positive y-axis. If the vertices are ordered counterclockwise (that is, according to positive orientation), the signed area is positive; otherwise, it is negative. In either case, the area formula is correct in absolute value. This is commonly called the shoelace formula or surveyor's formula.^[6]

The area A of a simple polygon can also be computed if the lengths of the sides, a₁, a₂, ..., a_n and the exterior angles, θ₁, θ₂, ..., θ_n are known, from:

${\displaystyle \begin{array}{r}A=\frac{1}{2}(a_1\\ \end{array}}$Zdroj:https://en.wikipedia.org?pojem=Polygon_edge
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---