Axiomatická teorie množin je označení pro teorii, která formalizuje vlastnosti množin takovým způsobem, aby bylo možné pomocí množin zkonstruovat všechny matematické objekty, takže dokazatelná tvrzení této teorie budou přesně odpovídat všem platným matematickým výsledkům ze všech oblastí matematiky (algebra, diferenciální rovnice, geometrie, teorie pravděpodobnosti i všechny ostatní).^[zdroj?

Hlavní význam takových teorií je v tom, že staví na velmi solidní základ pojem „dokazatelné matematické tvrzení“ a tedy poskytují užitečné vodítko při ověřování, zda nějaký matematický důkaz je korektní.^[zdroj?

Nejpoužívanější axiomatická teorie množin je jednak Zermelova-Fraenkelova teorie množin (značení ZF) a dále ZF s přidaným axiomem výběru (ta se značí ZF+AC nebo ZFC). ZFC je všeobecně uznávána jako teorie, která přesně popisuje platné matematické pravdy, tj. matematická věta je pokládána za pravdivou, právě když je dokazatelná v ZFC (dokazatelnost ovšem nelze snadno ověřit, neboť v každém okamžiku existuje mnoho pravdivých hypotéz, které ještě nebyly dokázány nebo ani vysloveny).^[zdroj?

Aplikace Gödelových vět o neúplnosti na axiomatickou teorii množin přináší vhledy na podstatu a filosofii matematiky, neboť z ní vyplývá, že sebelepší axiomatika teorie množin bude vždy obsahovat nerozhodnutelná tvrzení (množinu všech matematických pravd nelze popsat žádnou soustavou axiomů) a že pokud teorie, kterou chceme používat k popisu všech matematických pravd, je bezesporná, nelze tuto bezespornost dokázat.^[zdroj?

Důvod vzniku

K převážné většině matematických konstrukcí (včetně pokročilých, jako je úplný obal metrického prostoru) stačí intuitivní (naivní) teorie množin, v níž intuitivně pracujeme s množinami jako se souhrny objektů. Tento přístup však vede k rozporům, pokud pracujeme s „příliš velkými“ množinami (nejznámější z těchto sporů je Russelův paradox). Vzato do důsledků, naivní teorie množin je sporná a proto v ní lze dokázat cokoli (např. že 1+1=42).

V reakci na tyto rozpory vznikla axiomatická teorie množin, která staví dokazatelnost matematických pravd na pevný základ. Její hlavní přednosti oproti naivní teorii jsou tyto:

1. Neumožňuje Russelův paradox (a další paradoxy naivní teorie množin) tím, že velké souhrny objektů (například „souhrn všech množin“) v ní nejsou pokládány za množiny, nýbrž jsou nazývány vlastními třídami a pracuje se s nimi jinak.^[zdroj?

2. Nepředpokládá nic kromě přesně vyjmenovaných axiomů (odtud název „axiomatická“). Ani tak samozřejmé skutečnosti, jako že existuje prázdná množina (nebo že k množinám a, b existuje i množina {a,b}) není dovoleno předpokládat, dokud to není dokázáno z axiomů anebo samo není axiomem.

Predikátová logika dává návod, jak prohledáváním nekonečného stromu ověřit dokazatelnost tvrzení z dané množiny axiomů.^[zdroj? Existence soustavy axiomů, z nichž plyne každé matematické tvrzení, tedy umožňuje algoritmicky rozhodnout o pravdivosti jakékoli matematické hypotézy (tento algoritmus se nezastaví, pokud je tato hypotéza nerozhodnutelná z axiómů ZFC). To je sice v praxi nepoužitelné, protože počet větví stromu je astronomicky velký, ale přesto je ZFC užitečným vodítkem při diskuzi, zda nějaký argument lze nazvat platným matematickým důkazem.

Proč množiny?

Při konstrukci teorie, která má obsáhnout celou matematiku, není možné do ní přidat všechny druhy objektů – například přidat predikát „tento objekt univerza je přirozené číslo“ (podobně, jako GB má predikát „tento objekt je množina“) a vložit axiomy, které chování přirozených čísel popisují (např. Peanovy axiomy).

Při takovém přístupu by se množina predikátů a axiomů neustále rozrůstala, například po objevení komplexních čísel, hyperkomplexních čísel apod. S každým rozšířením by se musely znovu dokazovat výsledky o teorii dokázané (například to, že nějaké tvrzení je v této teorii nezávislé).^{[zdroj?[pozn 1]}

Proto je zvolen opačný přístup: axiomy popisují vlastnosti skupiny co nejjednodušších objektů, které stačí ke zkonstruování celé matematiky. Ukázalo se, že k tomuto účelu nejlépe slouží množiny; z těch lze zkonstruovat přirozená čísla, reálná čísla, funkce, přímky, topologické prostory atd.

Konstrukce objektů

Jelikož cílem ZF je popsat jedinou soustavou axiomů celou matematiku, není možné postupovat tak, že zavedeme pojem např. „přirozené číslo“ a vložíme axiomy o tom, jaké vlastnosti přirozená čísla mají. V takovém případě bychom museli rozšířit množinu axiomů pokaždé, když je v matematice objeven další důležitý pojem (reálné číslo, funkcionál, kategorie...)

Proto ZF vychází z předpokladu, že všechny matematické objekty jsou množiny, a její axiomy poskytují možnost z množin konstruovat množiny složitější. Prvek množin tedy mohou být opět jen množiny.

Matematické objekty, se kterými chceme pracovat, pak ztotožníme s vhodnými množinami – víme, jaké vlastnosti očekáváme od přirozených čísel (například že ke každému číslu existuje číslo o jedničku větší), a proto zvolíme množiny, které odpovídající vlastnost mají.

Uspořádané dvojice

Symbol (a, b) pokládáme za zkratku pro {{a}, {a, b}} .Tato definice splňuje základní vlastnost, kterou od uspořádaných dvojic čekáme:

(a, b) = (c, d) právě když a = c a zároveň b = d.

Přirozená čísla

• Číslo 0 ztotožníme s prázdnou množinou ${\displaystyle \emptyset }$
• Číslo 1 ztotožníme s množinou ${\displaystyle 0\cup \{0\}=\{\emptyset \}}$
• Číslo 2 ztotožníme s množinou ${\displaystyle 1\cup \{1\}=\{\emptyset ,\{\emptyset \}\}}$
• Číslo 3 ztotožníme s množinou ${\displaystyle 2\cup \{2\}=\{\emptyset ,\{\emptyset \},\{\emptyset ,\{\emptyset \}\}\}}$
• Obecně ${\displaystyle n+1=n\cup \{n\}}$

Formálně: Množinu přirozených čísel definujeme jako průnik všech množin, které obsahují prázdnou množinu a s každým svým prvkem ${\displaystyle x}$ obsahují i množinu ${\displaystyle x\cup \{x\}}$.

Množinu přirozených čísel (včetně nuly) značíme ${\displaystyle \omega _{0}}$.

Celá čísla

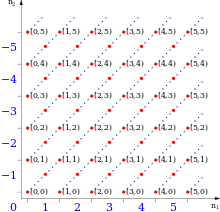
Máme-li definovaná přirozená čísla, pak by se mohlo zdát přirozené reprezentovat záporné číslo ${\displaystyle -n}$ jako ${\displaystyle (0,n)}$. To však nelze, protože pro některá přirozená čísla ${\displaystyle m,n}$ by mohlo platit ${\displaystyle m=(0,n)}$.

Je však možné reprezentovat přirozená čísla (pro ${\displaystyle n>=0}$) jako ${\displaystyle (0,n)}$ a záporná čísla ${\displaystyle -n}$ (pro ${\displaystyle n>0}$) jako ${\displaystyle (1,n)}$. Tato definice se nepoužívá, protože by definice sčítání, násobení apod. byla složitější, než u definice následující:

Idea je reprezentovat celé číslo ${\displaystyle z}$ nekonečnou množinou takových dvojic ${\displaystyle (a,b)}$, že ${\displaystyle a,b}$ jsou přirozená čísla splňující ${\displaystyle z=a-b}$. Například ${\displaystyle -2=\{(0,2),(1,3),(2,4),(3,5),....\}}$

Formálně: Množina celých čísel je definována jako rozklad (tedy množina všech tříd ekvivalence) kartézského součinu ${\displaystyle \omega _{0}}$ x ${\displaystyle \omega _{0}}$ podle ekvivalence:

${\displaystyle (a,b)}$ ~ ${\displaystyle (c,d)}$ právě když ${\displaystyle a+d=b+c}$.

Máme-li definované sčítání a násobení pro přirozená čísla, definujeme je pro celá čísla takto: vyberme libovolný prvek (tzv. reprezentant) ${\displaystyle (a,b)}$ a ${\displaystyle (c,d)}$ čísel, které chceme sečíst. Výsledkem bude třída ekvivalence, která obsahuje dvojici ${\displaystyle (e,f)}$ (tato třída nezávisí na volbě reprezentantů):

• Pro sčítání: ${\displaystyle e=a+c,f=b+d}$
• Pro násobení: ${\displaystyle e=a.c+b.d,f=a.d-b.c}$

Vzoreček pro násobení lze snadno odvodit roznásobením vztahu

${\displaystyle e-f=(a-b).(c-d)}$Zdroj:https://cs.wikipedia.org?pojem=New_Foundations
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---