In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot be undone, the simplest knot being a ring (or "unknot"). In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, ${\displaystyle \mathbb {E} ^{3}}$. Two mathematical knots are equivalent if one can be transformed into the other via a deformation of ${\displaystyle \mathbb {R} ^{3}}$ upon itself (known as an ambient isotopy); these transformations correspond to manipulations of a knotted string that do not involve cutting it or passing it through itself.

Knots can be described in various ways. Using different description methods, there may be more than one description of the same knot. For example, a common method of describing a knot is a planar diagram called a knot diagram, in which any knot can be drawn in many different ways. Therefore, a fundamental problem in knot theory is determining when two descriptions represent the same knot.

A complete algorithmic solution to this problem exists, which has unknown complexity.^[1] In practice, knots are often distinguished using a knot invariant, a "quantity" which is the same when computed from different descriptions of a knot. Important invariants include knot polynomials, knot groups, and hyperbolic invariants.

The original motivation for the founders of knot theory was to create a table of knots and links, which are knots of several components entangled with each other. More than six billion knots and links have been tabulated since the beginnings of knot theory in the 19th century.

To gain further insight, mathematicians have generalized the knot concept in several ways. Knots can be considered in other three-dimensional spaces and objects other than circles can be used; see knot (mathematics). For example, a higher-dimensional knot is an n-dimensional sphere embedded in (n+2)-dimensional Euclidean space.

History

Archaeologists have discovered that knot tying dates back to prehistoric times. Besides their uses such as recording information and tying objects together, knots have interested humans for their aesthetics and spiritual symbolism. Knots appear in various forms of Chinese artwork dating from several centuries BC (see Chinese knotting). The endless knot appears in Tibetan Buddhism, while the Borromean rings have made repeated appearances in different cultures, often representing strength in unity. The Celtic monks who created the Book of Kells lavished entire pages with intricate Celtic knotwork.

A mathematical theory of knots was first developed in 1771 by Alexandre-Théophile Vandermonde who explicitly noted the importance of topological features when discussing the properties of knots related to the geometry of position. Mathematical studies of knots began in the 19th century with Carl Friedrich Gauss, who defined the linking integral (Silver 2006). In the 1860s, Lord Kelvin's theory that atoms were knots in the aether led to Peter Guthrie Tait's creation of the first knot tables for complete classification. Tait, in 1885, published a table of knots with up to ten crossings, and what came to be known as the Tait conjectures. This record motivated the early knot theorists, but knot theory eventually became part of the emerging subject of topology.

These topologists in the early part of the 20th century—Max Dehn, J. W. Alexander, and others—studied knots from the point of view of the knot group and invariants from homology theory such as the Alexander polynomial. This would be the main approach to knot theory until a series of breakthroughs transformed the subject.

In the late 1970s, William Thurston introduced hyperbolic geometry into the study of knots with the hyperbolization theorem. Many knots were shown to be hyperbolic knots, enabling the use of geometry in defining new, powerful knot invariants. The discovery of the Jones polynomial by Vaughan Jones in 1984 (Sossinsky 2002, pp. 71–89), and subsequent contributions from Edward Witten, Maxim Kontsevich, and others, revealed deep connections between knot theory and mathematical methods in statistical mechanics and quantum field theory. A plethora of knot invariants have been invented since then, utilizing sophisticated tools such as quantum groups and Floer homology.

In the last several decades of the 20th century, scientists became interested in studying physical knots in order to understand knotting phenomena in DNA and other polymers. Knot theory can be used to determine if a molecule is chiral (has a "handedness") or not (Simon 1986). Tangles, strings with both ends fixed in place, have been effectively used in studying the action of topoisomerase on DNA (Flapan 2000). Knot theory may be crucial in the construction of quantum computers, through the model of topological quantum computation (Collins 2006).

Knot equivalence

On the left, the unknot, and a knot equivalent to it. It can be more difficult to determine whether complex knots, such as the one on the right, are equivalent to the unknot.

A knot is created by beginning with a one-dimensional line segment, wrapping it around itself arbitrarily, and then fusing its two free ends together to form a closed loop (Adams 2004) (Sossinsky 2002). Simply, we can say a knot ${\displaystyle K}$ is a "simple closed curve" (see Curve) — that is: a "nearly" injective and continuous function ${\displaystyle K\colon \to \mathbb {R} ^{3}}$, with the only "non-injectivity" being ${\displaystyle K(0)=K(1)}$. Topologists consider knots and other entanglements such as links and braids to be equivalent if the knot can be pushed about smoothly, without intersecting itself, to coincide with another knot.

The idea of knot equivalence is to give a precise definition of when two knots should be considered the same even when positioned quite differently in space. A formal mathematical definition is that two knots ${\displaystyle K_{1},K_{2}}$ are equivalent if there is an orientation-preserving homeomorphism ${\displaystyle h\colon \mathbb {R} ^{3}\to \mathbb {R} ^{3}}$ with ${\displaystyle h(K_{1})=K_{2}}$.

What this definition of knot equivalence means is that two knots are equivalent when there is a continuous family of homeomorphisms ${\displaystyle \{h_{t}:\mathbb {R} ^{3}\rightarrow \mathbb {R} ^{3}\ \mathrm {for} \ 0\leq t\leq 1\}}$ of space onto itself, such that the last one of them carries the first knot onto the second knot. (In detail: Two knots ${\displaystyle K_{1}}$ and ${\displaystyle K_{2}}$ are equivalent if there exists a continuous mapping ${\displaystyle H:\mathbb {R} ^{3}\times \rightarrow \mathbb {R} ^{3}}$ such that a) for each ${\displaystyle t\in }$ the mapping taking ${\displaystyle x\in \mathbb {R} ^{3}}$ to ${\displaystyle H(x,t)\in \mathbb {R} ^{3}}$ is a homeomorphism of ${\displaystyle \mathbb {R} ^{3}}$ onto itself; b) ${\displaystyle H(x,0)=x}$ for all ${\displaystyle x\in \mathbb {R} ^{3}}$; and c) ${\displaystyle H(K_{1},1)=K_{2}}$. Such a function ${\displaystyle H}$ is known as an ambient isotopy.)

These two notions of knot equivalence agree exactly about which knots are equivalent: Two knots that are equivalent under the orientation-preserving homeomorphism definition are also equivalent under the ambient isotopy definition, because any orientation-preserving homeomorphisms of ${\displaystyle \mathbb {R} ^{3}}$ to itself is the final stage of an ambient isotopy starting from the identity. Conversely, two knots equivalent under the ambient isotopy definition are also equivalent under the orientation-preserving homeomorphism definition, because the ${\displaystyle t=1}$ (final) stage of the ambient isotopy must be an orientation-preserving homeomorphism carrying one knot to the other.

The basic problem of knot theory, the recognition problem, is determining the equivalence of two knots. Algorithms exist to solve this problem, with the first given by Wolfgang Haken in the late 1960s (Hass 1998). Nonetheless, these algorithms can be extremely time-consuming, and a major issue in the theory is to understand how hard this problem really is (Hass 1998). The special case of recognizing the unknot, called the unknotting problem, is of particular interest (Hoste 2005). In February 2021 Marc Lackenby announced a new unknot recognition algorithm that runs in quasi-polynomial time.^[2]

Knot diagrams

A useful way to visualise and manipulate knots is to project the knot onto a plane—think of the knot casting a shadow on the wall. A small change in the direction of projection will ensure that it is one-to-one except at the double points, called crossings, where the "shadow" of the knot crosses itself once transversely (Rolfsen 1976). At each crossing, to be able to recreate the original knot, the over-strand must be distinguished from the under-strand. This is often done by creating a break in the strand going underneath. The resulting diagram is an immersed plane curve with the additional data of which strand is over and which is under at each crossing. (These diagrams are called knot diagrams when they represent a knot and link diagrams when they represent a link.) Analogously, knotted surfaces in 4-space can be related to immersed surfaces in 3-space.

A reduced diagram is a knot diagram in which there are no reducible crossings (also nugatory or removable crossings), or in which all of the reducible crossings have been removed.^[3][4] A petal projection is a type of projection in which, instead of forming double points, all strands of the knot meet at a single crossing point, connected to it by loops forming non-nested "petals".^[5]

Reidemeister moves

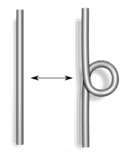
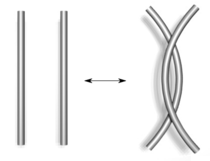
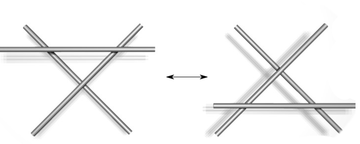
In 1927, working with this diagrammatic form of knots, J. W. Alexander and Garland Baird Briggs, and independently Kurt Reidemeister, demonstrated that two knot diagrams belonging to the same knot can be related by a sequence of three kinds of moves on the diagram, shown below. These operations, now called the Reidemeister moves, are:

Reidemeister moves

Type I	Type II
Type III

The proof that diagrams of equivalent knots are connected by Reidemeister moves relies on an analysis of what happens under the planar projection of the movement taking one knot to another. The movement can be arranged so that almost all of the time the projection will be a knot diagram, except at finitely many times when an "event" or "catastrophe" occurs, such as when more than two strands cross at a point or multiple strands become tangent at a point. A close inspection will show that complicated events can be eliminated, leaving only the simplest events: (1) a "kink" forming or being straightened out; (2) two strands becoming tangent at a point and passing through; and (3) three strands crossing at a point. These are precisely the Reidemeister moves (Sossinsky 2002, ch. 3) (Lickorish 1997, ch. 1).

Knot invariants

A knot invariant is a "quantity" that is the same for equivalent knots (Adams 2004) (Lickorish 1997) (Rolfsen 1976). For example, if the invariant is computed from a knot diagram, it should give the same value for two knot diagrams representing equivalent knots. An invariant may take the same value on two different knots, so by itself may be incapable of distinguishing all knots. An elementary invariant is tricolorability.

"Classical" knot invariants include the knot group, which is the fundamental group of the knot complement, and the Alexander polynomial, which can be computed from the Alexander invariant, a module constructed from the infinite cyclic cover of the knot complement (Lickorish 1997)(Rolfsen 1976). In the late 20th century, invariants such as "quantum" knot polynomials, Vassiliev invariants and hyperbolic invariants were discovered. These aforementioned invariants are only the tip of the iceberg of modern knot theory.

Knot polynomials

A knot polynomial is a knot invariant that is a polynomial. Well-known examples include the Jones and Alexander polynomials. A variant of the Alexander polynomial, the Alexander–Conway polynomial, is a polynomial in the variable z with integer coefficients (Lickorish 1997).

The Alexander–Conway polynomial is actually defined in terms of links, which consist of one or more knots entangled with each other. The concepts explained above for knots, e.g. diagrams and Reidemeister moves, also hold for links.

Consider an oriented link diagram, i.e. one in which every component of the link has a preferred direction indicated by an arrow. For a given crossing of the diagram, let ${\displaystyle L_{+},L_{-},L_{0}}$ be the oriented link diagrams resulting from changing the diagram as indicated in the figure:

The original diagram might be either ${\displaystyle L_{+}}$ or ${\displaystyle L_{-}}$, depending on the chosen crossing's configuration. Then the Alexander–Conway polynomial, ${\displaystyle C(z)}$, is recursively defined according to the rules:

• ${\displaystyle C(O)=1}$ (where ${\displaystyle O}$ is any diagram of the unknot)
• ${\displaystyle C({}_{}}$Zdroj:https://en.wikipedia.org?pojem=Knot_theory
  Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

  ---