Inverse sine

In mathematics, the inverse trigonometric functions (occasionally also called arcus functions,^[1]^[2]^[3]^[4]^[5] antitrigonometric functions^[6] or cyclometric functions^[7]^[8]^[9]) are the inverse functions of the trigonometric functions (with suitably restricted domains). Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions,^[10] and are used to obtain an angle from any of the angle's trigonometric ratios. Inverse trigonometric functions are widely used in engineering, navigation, physics, and geometry.

Notation

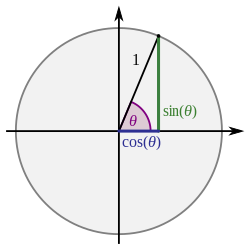
Several notations for the inverse trigonometric functions exist. The most common convention is to name inverse trigonometric functions using an arc- prefix: $arcsin(x)$ , $arccos(x)$ , $arctan(x)$ , etc.^[6] (This convention is used throughout this article.) This notation arises from the following geometric relationships:^{[citation needed]} when measuring in radians, an angle of $θ$ radians will correspond to an arc whose length is $rθ$ , where $r$ is the radius of the circle. Thus in the unit circle, the cosine of x function is both the arc and the angle, because the arc of a circle of radius 1 is the same as the angle. Or, "the arc whose cosine is $x$ " is the same as "the angle whose cosine is $x$ ", because the length of the arc of the circle in radii is the same as the measurement of the angle in radians.^[11] In computer programming languages, the inverse trigonometric functions are often called by the abbreviated forms asin, acos, atan.^[12]

The notations $sin -1 (x)$ , $cos -1 (x)$ , $tan -1 (x)$ , etc., as introduced by John Herschel in 1813,^[13]^[14] are often used as well in English-language sources,^[6] much more than the also established $sin (x)$ , $cos (x)$ , $tan (x)$ – conventions consistent with the notation of an inverse function, that is useful (for example) to define the multivalued version of each inverse trigonometric function: $\tan ^{-1}(x)=\{\arctan(x)+\pi k\mid k\in \mathbb {Z} \}~.$ However, this might appear to conflict logically with the common semantics for expressions such as $sin 2 (x)$ (although only $sin 2 x$ , without parentheses, is the really common use), which refer to numeric power rather than function composition, and therefore may result in confusion between notation for the reciprocal (multiplicative inverse) and inverse function.^[15]

The confusion is somewhat mitigated by the fact that each of the reciprocal trigonometric functions has its own name — for example, $(cos(x)) -1 = sec(x)$ . Nevertheless, certain authors advise against using it, since it is ambiguous.^[6]^[16] Another precarious convention used by a small number of authors is to use an uppercase first letter, along with a “ $-1$ ” superscript: $Sin -1 (x)$ , $Cos -1 (x)$ , $Tan -1 (x)$ , etc.^[17] Although it is intended to avoid confusion with the reciprocal, which should be represented by $sin -1 (x)$ , $cos -1 (x)$ , etc., or, better, by $sin -1 x$ , $cos -1 x$ , etc., it in turn creates yet another major source of ambiguity, especially since many popular high-level programming languages (e.g. Mathematica and MAGMA) use those very same capitalised representations for the standard trig functions, whereas others (Python, SymPy, NumPy, Matlab, MAPLE, etc.) use lower-case.

Hence, since 2009, the ISO 80000-2 standard has specified solely the "arc" prefix for the inverse functions.

Basic concepts

The points labelled 1, Sec(θ), Csc(θ) represent the length of the line segment from the origin to that point. Sin(θ), Tan(θ), and 1 are the heights to the line starting from the $x$ -axis, while Cos(θ), 1, and Cot(θ) are lengths along the $x$ -axis starting from the origin.

Principal values

Since none of the six trigonometric functions are one-to-one, they must be restricted in order to have inverse functions. Therefore, the result ranges of the inverse functions are proper (i.e. strict) subsets of the domains of the original functions.

For example, using function in the sense of multivalued functions, just as the square root function $y={\sqrt {x}}$ could be defined from $y^{2}=x,$ the function $y=\arcsin(x)$ is defined so that $\sin(y)=x.$ For a given real number $x,$ with $-1\leq x\leq 1,$ there are multiple (in fact, countably infinitely many) numbers $y$ such that $\sin(y)=x$ ; for example, $\sin(0)=0,$ but also $\sin(\pi )=0,$ $\sin(2\pi )=0,$ etc. When only one value is desired, the function may be restricted to its principal branch. With this restriction, for each $x$ in the domain, the expression $\arcsin(x)$ will evaluate only to a single value, called its principal value. These properties apply to all the inverse trigonometric functions.

The principal inverses are listed in the following table.

Name	Usual notation	Definition	Domain of $x$ for real result	Range of usual principal value (radians)	Range of usual principal value (degrees)
arcsine	$y=\arcsin(x)$	$x = sin (y)$	$-1\leq x\leq 1$	$-{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}}$	$-90^{\circ }\leq y\leq 90^{\circ }$
arccosine	$y=\arccos(x)$	$x = cos (y)$	$-1\leq x\leq 1$	$0\leq y\leq \pi$	$0^{\circ }\leq y\leq 180^{\circ }$
arctangent	$y=\arctan(x)$

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]