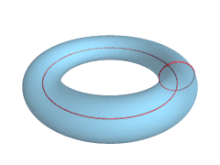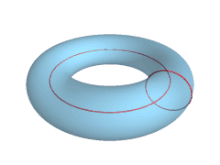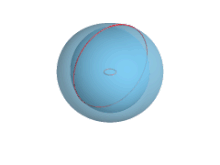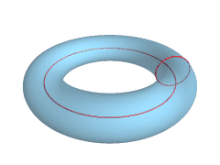
In geometry, a torus (pl.: tori or toruses) is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanar with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a donut or doughnut.

If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution, also known as a ring torus. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a spindle torus (or self-crossing torus or self-intersecting torus). If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a toroid, as in a square toroid.

Real-world objects that approximate a torus of revolution include swim rings, inner tubes and ringette rings.

A torus should not be confused with a solid torus, which is formed by rotating a disk, rather than a circle, around an axis. A solid torus is a torus plus the volume inside the torus. Real-world objects that approximate a solid torus include O-rings, non-inflatable lifebuoys, ring doughnuts, and bagels.

In topology, a ring torus is homeomorphic to the Cartesian product of two circles: ${\displaystyle S^{1}\times S^{1}}$, and the latter is taken to be the definition in that context. It is a compact 2-manifold of genus 1. The ring torus is one way to embed this space into Euclidean space, but another way to do this is the Cartesian product of the embedding of ${\displaystyle S^{1}}$ in the plane with itself. This produces a geometric object called the Clifford torus, a surface in 4-space.

In the field of topology, a torus is any topological space that is homeomorphic to a torus.^[1] The surface of a coffee cup and a doughnut are both topological tori with genus one.

An example of a torus can be constructed by taking a rectangular strip of flexible material such as rubber, and joining the top edge to the bottom edge, and the left edge to the right edge, without any half-twists (compare Klein bottle).

Etymology

Torus is a Latin word for "a round, swelling, elevation, protuberance".

Geometry

Bottom-halves and
vertical cross-sections

R > r: ring torus or anchor ring

R=r: horn torus

R < r: self-intersecting spindle torus

A torus can be parametrized as:^[2]

$${\displaystyle {\begin{aligned}x(\theta ,\varphi )&=(R+r\cos \theta )\cos {\varphi }\\y(\theta ,\varphi )&=(R+r\cos \theta )\sin {\varphi }\\z(\theta ,\varphi )&=r\sin \theta \\\end{aligned}}}$$

using angular coordinates ${\displaystyle \theta ,\varphi \in 0,2\pi ),}$ representing rotation around the tube and rotation around the torus' axis of revolution, respectively, where the major radius ${\displaystyle R}$ is the distance from the center of the tube to the center of the torus and the minor radius ${\displaystyle r}$ is the radius of the tube.^[3]

The ratio ${\displaystyle R/r}$ is called the aspect ratio of the torus. The typical doughnut confectionery has an aspect ratio of about 3 to 2.

An implicit equation in Cartesian coordinates for a torus radially symmetric about the ${\displaystyle z}$-axis is

$${\displaystyle {\textstyle {\bigl (}{\sqrt {x^{2}+y^{2}}}-R{\bigr )}^{2}}+z^{2}=r^{2}.}$$

Algebraically eliminating the square root gives a quartic equation,

$${\displaystyle \left(x^{2}+y^{2}+z^{2}+R^{2}-r^{2}\right)^{2}=4R^{2}\left(x^{2}+y^{2}\right).}$$

The three classes of standard tori correspond to the three possible aspect ratios between R and r:

• When R > r, the surface will be the familiar ring torus or anchor ring.
• R = r corresponds to the horn torus, which in effect is a torus with no "hole".
• R < r describes the self-intersecting spindle torus; its inner shell is a lemon and its outer shell is an apple
• When R = 0, the torus degenerates to the sphere.

When R ≥ r, the interior

$${\displaystyle {\textstyle {\bigl (}{\sqrt {x^{2}+y^{2}}}-R{\bigr )}^{2}}+z^{2}<r^{2}}$$

$${\displaystyle {\begin{aligned}A&=\left(2\pi r\right)\left(2\pi R\right)=4\pi ^{2}Rr,\\5muV&=\left(\pi r^{2}\right)\left(2\pi R\right)=2\pi ^{2}Rr^{2}.\end{aligned}}}$$

These formulas are the same as for a cylinder of length 2πR and radius r, obtained from cutting the tube along the plane of a small circle, and unrolling it by straightening out (rectifying) the line running around the center of the tube. The losses in surface area and volume on the inner side of the tube exactly cancel out the gains on the outer side.

Expressing the surface area and the volume by the distance p of an outermost point on the surface of the torus to the center, and the distance q of an innermost point to the center (so that R = p + q/2 and r = p − q/2), yields

$${\displaystyle {\begin{aligned}A&=4\pi ^{2}\left({\frac {p+q}{2}}\right)\left({\frac {p-q}{2}}\right)=\pi ^{2}(p+q)(p-q),\\5muV&=2\pi ^{2}\left({\frac {p+q}{2}}\right)\left({\frac {p-q}{2}}\right)^{2}={\tfrac {1}{4}}\pi ^{2}(p+q)(p-q)^{2}.\end{aligned}}}$$

As a torus is the product of two circles, a modified version of the spherical coordinate system is sometimes used. In traditional spherical coordinates there are three measures, R, the distance from the center of the coordinate system, and θ and φ, angles measured from the center point.

As a torus has, effectively, two center points, the centerpoints of the angles are moved; φ measures the same angle as it does in the spherical system, but is known as the "toroidal" direction. The center point of θ is moved to the center of r, and is known as the "poloidal" direction. These terms were first used in a discussion of the Earth's magnetic field, where "poloidal" was used to denote "the direction toward the poles".^[5]

In modern use, toroidal and poloidal are more commonly used to discuss magnetic confinement fusion devices.

Topologyedit

This section includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this section by introducing more precise citations. (November 2015) (Learn how and when to remove this message)

Topologically, a torus is a closed surface defined as the product of two circles: S¹ × S¹. This can be viewed as lying in C² and is a subset of the 3-sphere S³ of radius √2. This topological torus is also often called the Clifford torus. In fact, S³ is filled out by a family of nested tori in this manner (with two degenerate circles), a fact which is important in the study of S³ as a fiber bundle over S² (the Hopf bundle).

The surface described above, given the relative topology from ${\displaystyle {\mathbb{R}}^3}$Zdroj:https://en.wikipedia.org?pojem=Flat_torus
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.