Distributive law

Distributive property
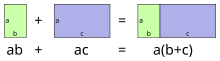	Visualization of distributive law for positive numbers
Type	Law, rule of replacement
Field	Elementary algebra; Boolean algebra; Abstract algebra; Set theory; Propositional calculus;
Symbolic statement	Elementary algebra ; Propositional calculus: ; ; ;

In mathematics, the distributive property of binary operations is a generalization of the distributive law, which asserts that the equality

x\cdot (y+z)=x\cdot y+x\cdot z

is always true in elementary algebra. For example, in elementary arithmetic, one has

2\cdot (1+3)=(2\cdot 1)+(2\cdot 3).

Therefore, one would say that multiplication distributes over addition.

This basic property of numbers is part of the definition of most algebraic structures that have two operations called addition and multiplication, such as complex numbers, polynomials, matrices, rings, and fields. It is also encountered in Boolean algebra and mathematical logic, where each of the logical and (denoted $\,\land \,$ ) and the logical or (denoted $\,\lor \,$ ) distributes over the other.

Definition

Given a set $S$ and two binary operators $\,*\,$ and $\,+\,$ on $S,$

the operation $\,*\,$ is left-distributive over (or with respect to) $\,+\,$ if, given any elements $x,y,{\text{ and }}z$ of $S,$

x*(y+z)=(x*y)+(x*z);

the operation $\,*\,$ is right-distributive over $\,+\,$ if, given any elements $x,y,{\text{ and }}z$ of $S,$

(y+z)*x=(y*x)+(z*x);

and the operation $\,*\,$ is distributive over $\,+\,$ if it is left- and right-distributive.^[1]

When $\,*\,$ is commutative, the three conditions above are logically equivalent.

Meaning

The operators used for examples in this section are those of the usual addition $\,+\,$ and multiplication $\,\cdot .\,$

If the operation denoted $\cdot$ is not commutative, there is a distinction between left-distributivity and right-distributivity:

a\cdot \left(b\pm c\right)=a\cdot b\pm a\cdot c\qquad {\text{ (left-distributive) }}

(a\pm b)\cdot c=a\cdot c\pm b\cdot c\qquad {\text{ (right-distributive) }}.

In either case, the distributive property can be described in words as:

To multiply a sum (or difference) by a factor, each summand (or minuend and subtrahend) is multiplied by this factor and the resulting products are added (or subtracted).

If the operation outside the parentheses (in this case, the multiplication) is commutative, then left-distributivity implies right-distributivity and vice versa, and one talks simply of distributivity.

One example of an operation that is "only" right-distributive is division, which is not commutative:

(a\pm b)\div c=a\div c\pm b\div c.

In this case, left-distributivity does not apply:

a\div (b\pm c)\neq a\div b\pm a\div c

The distributive laws are among the axioms for rings (like the ring of integers) and fields (like the field of rational numbers). Here multiplication is distributive over addition, but addition is not distributive over multiplication. Examples of structures with two operations that are each distributive over the other are Boolean algebras such as the algebra of sets or the switching algebra.

Multiplying sums can be put into words as follows: When a sum is multiplied by a sum, multiply each summand of a sum with each summand of the other sum (keeping track of signs) then add up all of the resulting products.

Examples

Real numbers

In the following examples, the use of the distributive law on the set of real numbers $\mathbb {R}$ is illustrated. When multiplication is mentioned in elementary mathematics, it usually refers to this kind of multiplication. From the point of view of algebra, the real numbers form a field, which ensures the validity of the distributive law.

First example (mental and written multiplication): During mental arithmetic, distributivity is often used unconsciously: $6\cdot 16=6\cdot (10+6)=6\cdot 10+6\cdot 6=60+36=96$ Thus, to calculate $6\cdot 16$ in one's head, one first multiplies $6\cdot 10$ and $6\cdot 6$ and add the intermediate results. Written multiplication is also based on the distributive law.
Second example (with variables): $3a^{2}b\cdot (4a-5b)=3a^{2}b\cdot 4a-3a^{2}b\cdot 5b=12a^{3}b-15a^{2}b^{2}$

[1]