Discrete calculus or the calculus of discrete functions, is the mathematical study of incremental change, in the same way that geometry is the study of shape and algebra is the study of generalizations of arithmetic operations. The word calculus is a Latin word, meaning originally "small pebble"; as such pebbles were used for calculation, the meaning of the word has evolved and today usually means a method of computation. Meanwhile, calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the study of continuous change.

Discrete calculus has two entry points, differential calculus and integral calculus. Differential calculus concerns incremental rates of change and the slopes of piece-wise linear curves. Integral calculus concerns accumulation of quantities and the areas under piece-wise constant curves. These two points of view are related to each other by the fundamental theorem of discrete calculus.

The study of the concepts of change starts with their discrete form. The development is dependent on a parameter, the increment ${\displaystyle \Delta x}$ of the independent variable. If we so choose, we can make the increment smaller and smaller and find the continuous counterparts of these concepts as limits. Informally, the limit of discrete calculus as ${\displaystyle \Delta x\to 0}$ is infinitesimal calculus. Even though it serves as a discrete underpinning of calculus, the main value of discrete calculus is in applications.

Two initial constructions

Discrete differential calculus is the study of the definition, properties, and applications of the difference quotient of a function. The process of finding the difference quotient is called differentiation. Given a function defined at several points of the real line, the difference quotient at that point is a way of encoding the small-scale (i.e., from the point to the next) behavior of the function. By finding the difference quotient of a function at every pair of consecutive points in its domain, it is possible to produce a new function, called the difference quotient function or just the difference quotient of the original function. In formal terms, the difference quotient is a linear operator which takes a function as its input and produces a second function as its output. This is more abstract than many of the processes studied in elementary algebra, where functions usually input a number and output another number. For example, if the doubling function is given the input three, then it outputs six, and if the squaring function is given the input three, then it outputs nine. The derivative, however, can take the squaring function as an input. This means that the derivative takes all the information of the squaring function—such as that two is sent to four, three is sent to nine, four is sent to sixteen, and so on—and uses this information to produce another function. The function produced by differentiating the squaring function turns out to be something close to the doubling function.

Suppose the functions are defined at points separated by an increment ${\displaystyle \Delta x=h>0}$:

${\displaystyle a,a+h,a+2h,\ldots ,a+nh,\ldots }$

The "doubling function" may be denoted by ${\displaystyle g(x)=2x}$ and the "squaring function" by ${\displaystyle f(x)=x^{2}}$. The "difference quotient" is the rate of change of the function over one of the intervals ${\displaystyle }$ defined by the formula:

${\displaystyle {\frac {f(x+h)-f(x)}{h}}.}$

It takes the function ${\displaystyle f}$ as an input, that is all the information—such as that two is sent to four, three is sent to nine, four is sent to sixteen, and so on—and uses this information to output another function, the function ${\displaystyle g(x)=2x+h}$, as will turn out. As a matter of convenience, the new function may defined at the middle points of the above intervals:

${\displaystyle a+h/2,a+h+h/2,a+2h+h/2,...,a+nh+h/2,...}$

As the rate of change is that for the whole interval ${\displaystyle }$, any point within it can be used as such a reference or, even better, the whole interval which makes the difference quotient a ${\displaystyle 1}$-cochain.

The most common notation for the difference quotient is:

${\displaystyle {\frac {\Delta f}{\Delta x}}(x+h/2)={\frac {f(x+h)-f(x)}{h}}.}$

If the input of the function represents time, then the difference quotient represents change with respect to time. For example, if ${\displaystyle f}$ is a function that takes a time as input and gives the position of a ball at that time as output, then the difference quotient of ${\displaystyle f}$ is how the position is changing in time, that is, it is the velocity of the ball.

If a function is linear (that is, if the points of the graph of the function lie on a straight line), then the function can be written as ${\displaystyle y=mx+b}$, where ${\displaystyle x}$ is the independent variable, ${\displaystyle y}$ is the dependent variable, ${\displaystyle b}$ is the ${\displaystyle y}$-intercept, and:

${\displaystyle m={\frac {\text{rise}}{\text{run}}}={\frac {{\text{change in }}y}{{\text{change in }}x}}={\frac {\Delta y}{\Delta x}}.}$

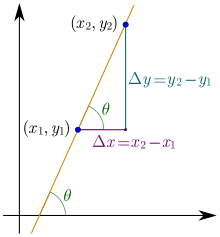
This gives an exact value for the slope of a straight line.

If the function is not linear, however, then the change in ${\displaystyle y}$ divided by the change in ${\displaystyle x}$ varies. The difference quotient give an exact meaning to the notion of change in output with respect to change in input. To be concrete, let ${\displaystyle f}$ be a function, and fix a point ${\displaystyle x}$ in the domain of ${\displaystyle f}$. ${\displaystyle (x,f(x))}$ is a point on the graph of the function. If ${\displaystyle h}$ is the increment of ${\displaystyle x}$, then ${\displaystyle x+h}$ is the next value of ${\displaystyle x}$. Therefore, ${\displaystyle (x+h,f(x+h))}$ is the increment of ${\displaystyle (x,f(x))}$. The slope of the line between these two points is

${\displaystyle m={\frac {f(x+h)-f(x)}{(x+h)-x}}={\frac {f(x+h)-f(x)}{h}}.}$

So ${\displaystyle m}$ is the slope of the line between ${\displaystyle (x,f(x))}$ and ${\displaystyle (x+h,f(x+h))}$.

Here is a particular example, the difference quotient of the squaring function. Let ${\displaystyle f(x)=x^{2}}$ be the squaring function. Then:

Zdroj:https://en.wikipedia.org?pojem=Discrete_calculus
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---