This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (January 2022) (Learn how and when to remove this message)

In physics, the cross section is a measure of the probability that a specific process will take place in a collision of two particles. For example, the Rutherford cross-section is a measure of probability that an alpha particle will be deflected by a given angle during an interaction with an atomic nucleus. Cross section is typically denoted σ (sigma) and is expressed in units of area, more specifically in barns. In a way, it can be thought of as the size of the object that the excitation must hit in order for the process to occur, but more exactly, it is a parameter of a stochastic process.

When two discrete particles interact in classical physics, their mutual cross section is the area transverse to their relative motion within which they must meet in order to scatter from each other. If the particles are hard inelastic spheres that interact only upon contact, their scattering cross section is related to their geometric size. If the particles interact through some action-at-a-distance force, such as electromagnetism or gravity, their scattering cross section is generally larger than their geometric size.

When a cross section is specified as the differential limit of a function of some final-state variable, such as particle angle or energy, it is called a differential cross section (see detailed discussion below). When a cross section is integrated over all scattering angles (and possibly other variables), it is called a total cross section or integrated total cross section. For example, in Rayleigh scattering, the intensity scattered at the forward and backward angles is greater than the intensity scattered sideways, so the forward differential scattering cross section is greater than the perpendicular differential cross section, and by adding all of the infinitesimal cross sections over the whole range of angles with integral calculus, we can find the total cross section.

Scattering cross sections may be defined in nuclear, atomic, and particle physics for collisions of accelerated beams of one type of particle with targets (either stationary or moving) of a second type of particle. The probability for any given reaction to occur is in proportion to its cross section. Thus, specifying the cross section for a given reaction is a proxy for stating the probability that a given scattering process will occur.

The measured reaction rate of a given process depends strongly on experimental variables such as the density of the target material, the intensity of the beam, the detection efficiency of the apparatus, or the angle setting of the detection apparatus. However, these quantities can be factored away, allowing measurement of the underlying two-particle collisional cross section.

Differential and total scattering cross sections are among the most important measurable quantities in nuclear, atomic, and particle physics.

With light scattering off of a particle, the cross section specifies the amount of optical power scattered from light of a given irradiance (power per area). It is important to note that although the cross section has the same units as area, the cross section may not necessarily correspond to the actual physical size of the target given by other forms of measurement. It is not uncommon for the actual cross-sectional area of a scattering object to be much larger or smaller than the cross section relative to some physical process. For example, plasmonic nanoparticles can have light scattering cross sections for particular frequencies that are much larger than their actual cross-sectional areas.

Collision among gas particles

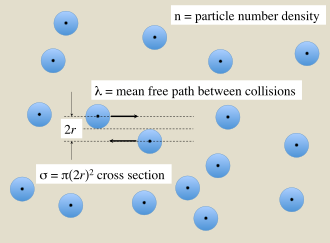
In a gas of finite-sized particles there are collisions among particles that depend on their cross-sectional size. The average distance that a particle travels between collisions depends on the density of gas particles. These quantities are related by

${\displaystyle \sigma ={\frac {1}{n\lambda }},}$

where

σ is the cross section of a two-particle collision (SI unit: m²),

λ is the mean free path between collisions (SI unit: m),

n is the number density of the target particles (SI unit: m⁻³).

If the particles in the gas can be treated as hard spheres of radius r that interact by direct contact, as illustrated in Figure 1, then the effective cross section for the collision of a pair is

${\displaystyle \sigma =\pi \left(2r\right)^{2}}$

If the particles in the gas interact by a force with a larger range than their physical size, then the cross section is a larger effective area that may depend on a variety of variables such as the energy of the particles.

Cross sections can be computed for atomic collisions but also are used in the subatomic realm. For example, in nuclear physics a "gas" of low-energy neutrons collides with nuclei in a reactor or other nuclear device, with a cross section that is energy-dependent and hence also with well-defined mean free path between collisions.

Attenuation of a beam of particles

If a beam of particles enters a thin layer of material of thickness dz, the flux Φ of the beam will decrease by dΦ according to

${\displaystyle {\frac {\mathrm {d} \Phi }{\mathrm {d} z}}=-n\sigma \Phi ,}$

where σ is the total cross section of all events, including scattering, absorption, or transformation to another species. The volumetric number density of scattering centers is designated by n. Solving this equation exhibits the exponential attenuation of the beam intensity:

${\displaystyle \Phi =\Phi _{0}e^{-n\sigma z},}$

where Φ₀ is the initial flux, and z is the total thickness of the material. For light, this is called the Beer–Lambert law.

Differential cross section

Consider a classical measurement where a single particle is scattered off a single stationary target particle. Conventionally, a spherical coordinate system is used, with the target placed at the origin and the z axis of this coordinate system aligned with the incident beam. The angle θ is the scattering angle, measured between the incident beam and the scattered beam, and the φ is the azimuthal angle.

The impact parameter b is the perpendicular offset of the trajectory of the incoming particle, and the outgoing particle emerges at an angle θ. For a given interaction (coulombic, magnetic, gravitational, contact, etc.), the impact parameter and the scattering angle have a definite one-to-one functional dependence on each other. Generally the impact parameter can neither be controlled nor measured from event to event and is assumed to take all possible values when averaging over many scattering events. The differential size of the cross section is the area element in the plane of the impact parameter, i.e. dσ = b dφ db. The differential angular range of the scattered particle at angle θ is the solid angle element dΩ = sin θ dθ dφ. The differential cross section is the quotient of these quantities, dσ/dΩ.

It is a function of the scattering angle (and therefore also the impact parameter), plus other observables such as the momentum of the incoming particle. The differential cross section is always taken to be positive, even though larger impact parameters generally produce less deflection. In cylindrically symmetric situations (about the beam axis), the azimuthal angle φ is not changed by the scattering process, and the differential cross section can be written as

${\displaystyle {\frac {\mathrm {d} \sigma }{\mathrm {d} (\cos \theta )}}=\int _{0}^{2\pi }{\frac {\mathrm {d} \sigma }{\mathrm {d} \Omega }}\,\mathrm {d} \varphi }$.

In situations where the scattering process is not azimuthally symmetric, such as when the beam or target particles possess magnetic moments oriented perpendicular to the beam axis, the differential cross section must also be expressed as a function of the azimuthal angle.

For scattering of particles of incident flux F_inc off a stationary target consisting of many particles, the differential cross section dσ/dΩ at an angle (θ,φ) is related to the flux of scattered particle detection F_out(θ,φ) in particles per unit time by

${\displaystyle {\frac {\mathrm {d} \sigma }{\mathrm {d} \Omega }}(\theta ,\varphi )={\frac {1}{nt\Delta \Omega }}{\frac {F_{\text{out}}(\theta ,\varphi )}{F_{\text{inc}}}}.}$

Here ΔΩ is the finite angular size of the detector (SI unit: sr), n is the number density of the target particles (SI unit: m⁻³), and t is the thickness of the stationary target (SI unit: m). This formula assumes that the target is thin enough that each beam particle will interact with at most one target particle.

The total cross section σ may be recovered by integrating the differential cross section dσ/dΩ over the full solid angle (4π steradians):

${\displaystyle \sigma =\oint _{4\pi }{\frac {\mathrm {d} \sigma }{\mathrm {d} \Omega }}\,\mathrm {d} \Omega =\int _{0}^{2\pi }\int _{0}^{\pi }{\frac {\mathrm {d} \sigma }{\mathrm {d} \Omega }}\sin \theta \,\mathrm {d} \theta \,\mathrm {d} \varphi .}$

It is common to omit the "differential" qualifier when the type of cross section can be inferred from context. In this case, σ may be referred to as the integral cross section or total cross section. The latter term may be confusing in contexts where multiple events are involved, since "total" can also refer to the sum of cross sections over all events.

The differential cross section is extremely useful quantity in many fields of physics, as measuring it can reveal a great amount of information about the internal structure of the target particles. For example, the differential cross section of Rutherford scattering provided strong evidence for the existence of the atomic nucleus.

Instead of the solid angle, the momentum transfer may be used as the independent variable of differential cross sections.

Differential cross sections in inelastic scattering contain resonance peaks that indicate the creation of metastable states and contain information about their energy and lifetime.

Quantum scattering

In the time-independent formalism of quantum scattering, the initial wave function (before scattering) is taken to be a plane wave with definite momentum k:

${\displaystyle \phi _{-}(\mathbf {r} )\;{\stackrel {r\to \infty }{\longrightarrow }}\;e^{ikz},}$

where z and r are the relative coordinates between the projectile and the target. The arrow indicates that this only describes the asymptotic behavior of the wave function when the projectile and target are too far apart for the interaction to have any effect.

After scattering takes place it is expected that the wave function takes on the following asymptotic form:

${\displaystyle \phi _{+}(\mathbf {r} )\;{\stackrel {r\to \infty }{\longrightarrow }}\;f(\theta ,\phi ){\frac {e^{ikr}}{r}},}$

where f is some function of the angular coordinates known as the scattering amplitude. This general form is valid for any short-ranged, energy-conserving interaction. It is not true for long-ranged interactions, so there are additional complications when dealing with electromagnetic interactions.

The full wave function of the system behaves asymptotically as the sum

${\displaystyle \phi (\mathbf {r} )\;{\stackrel {r\to \infty }{\longrightarrow }}\;\phi _{-}(\mathbf {r} )+\phi _{+}(\mathbf {r} ).}$

The differential cross section is related to the scattering amplitude:

${\displaystyle {\frac {\mathrm {d} \sigma }{\mathrm {d} \Omega }}(\theta ,\phi )={\bigl |}f(\theta ,\phi ){\bigr |}^{2}.}$

This has the simple interpretation as the probability density for finding the scattered projectile at a given angle.

A cross section is therefore a measure of the effective surface area seen by the impinging particles, and as such is expressed in units of area. The cross section of two particles (i.e. observed when the two particles are colliding with each other) is a measure of the interaction event between the two particles. The cross section is proportional to the probability that an interaction will occur; for example in a simple scattering experiment the number of particles scattered per unit of time (current of scattered particles I_r) depends only on the number of incident particles per unit of time (current of incident particles I_i), the characteristics of target (for example the number of particles per unit of surface N), and the type of interaction. For Nσ ≪ 1 we have

Zdroj:https://en.wikipedia.org?pojem=Differential_cross_section
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

---