In logic and mathematics, contraposition, or transposition, refers to the inference of going from a conditional statement into its logically equivalent contrapositive, and an associated proof method known as § Proof by contrapositive. The contrapositive of a statement has its antecedent and consequent inverted and flipped.

Conditional statement ${\displaystyle P\rightarrow Q}$. In formulas: the contrapositive of ${\displaystyle P\rightarrow Q}$ is ${\displaystyle \neg Q\rightarrow \neg P}$.^[1]

If P, Then Q. — If not Q, Then not P. "If it is raining, then I wear my coat" — "If I don't wear my coat, then it isn't raining."

The law of contraposition says that a conditional statement is true if, and only if, its contrapositive is true.^[2]

The contrapositive (${\displaystyle \neg Q\rightarrow \neg P}$) can be compared with three other statements:

Inversion (the inverse), ${\displaystyle \neg P\rightarrow \neg Q}$

"If it is not raining, then I don't wear my coat." Unlike the contrapositive, the inverse's truth value is not at all dependent on whether or not the original proposition was true, as evidenced here.

Conversion (the converse), ${\displaystyle Q\rightarrow P}$

"If I wear my coat, then it is raining." The converse is actually the contrapositive of the inverse, and so always has the same truth value as the inverse (which as stated earlier does not always share the same truth value as that of the original proposition).

Negation (the logical complement), ${\displaystyle \neg (P\rightarrow Q)}$

"It is not the case that if it is raining then I wear my coat.", or equivalently, "Sometimes, when it is raining, I don't wear my coat. " If the negation is true, then the original proposition (and by extension the contrapositive) is false.

Note that if ${\displaystyle P\rightarrow Q}$ is true and one is given that ${\displaystyle Q}$ is false (i.e., ${\displaystyle \neg Q}$), then it can logically be concluded that ${\displaystyle P}$ must be also false (i.e., ${\displaystyle \neg P}$). This is often called the law of contrapositive, or the modus tollens rule of inference.^[3]

Intuitive explanation

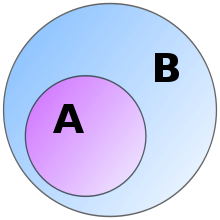
In the Euler diagram shown, if something is in A, it must be in B as well. So we can interpret "all of A is in B" as:

${\displaystyle A\to B}$

It is also clear that anything that is not within B (the blue region) cannot be within A, either. This statement, which can be expressed as:

${\displaystyle \neg B\to \neg A}$

is the contrapositive of the above statement. Therefore, one can say that

${\displaystyle (A\to B)\leftrightarrow (\neg B\to \neg A).}$

In practice, this equivalence can be used to make proving a statement easier. For example, if one wishes to prove that every girl in the United States (A) has brown hair (B), one can either try to directly prove ${\displaystyle A\to B}$ by checking that all girls in the United States do indeed have brown hair, or try to prove ${\displaystyle \neg B\to \neg A}$ by checking that all girls without brown hair are indeed all outside the US. In particular, if one were to find at least one girl without brown hair within the US, then one would have disproved ${\displaystyle \neg B\to \neg A}$, and equivalently ${\displaystyle A\to B}$.

In general, for any statement where A implies B, not B always implies not A. As a result, proving or disproving either one of these statements automatically proves or disproves the other, as they are logically equivalent to each other.

Formal definition

A proposition Q is implicated by a proposition P when the following relationship holds:

${\displaystyle (P\to Q)}$

This states that, "if ${\displaystyle P}$, then ${\displaystyle Q}$", or, "if Socrates is a man, then Socrates is human." In a conditional such as this, ${\displaystyle P}$ is the antecedent, and ${\displaystyle Q}$ is the consequent. One statement is the contrapositive of the other only when its antecedent is the negated consequent of the other, and vice versa. Thus a contrapositive generally takes the form of:

${\displaystyle (\neg Q\to \neg P).}$

That is, "If not-${\displaystyle Q}$, then not-${\displaystyle P}$", or, more clearly, "If ${\displaystyle Q}$ is not the case, then P is not the case." Using our example, this is rendered as "If Socrates is not human, then Socrates is not a man." This statement is said to be contraposed to the original and is logically equivalent to it. Due to their logical equivalence, stating one effectively states the other; when one is true, the other is also true, and when one is false, the other is also false.

Strictly speaking, a contraposition can only exist in two simple conditionals. However, a contraposition may also exist in two complex, universal conditionals, if they are similar. Thus, ${\displaystyle \forall {x}(P{x}\to Q{x})}$, or "All ${\displaystyle P}$s are ${\displaystyle Q}$s," is contraposed to ${\displaystyle \forall {x}(\neg Q{x}\to \neg P{x})}$, or "All non-${\displaystyle Q}$s are non-${\displaystyle P}$s."^[4]

Sequent notation

The transposition rule may be expressed as a sequent:

${\displaystyle (P\to Q)\vdash (\neg Q\to \neg P),}$

where ${\displaystyle \vdash }$ is a metalogical symbol meaning that $$Zdroj:https://en.wikipedia.org?pojem=Contrapositive_(logic)
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.