Part of a series on statistics
Probability theory
Probability Axioms Determinism System Indeterminism Randomness
Probability space Sample space Event Collectively exhaustive events Elementary event Mutual exclusivity Outcome Singleton Experiment Bernoulli trial Probability distribution Bernoulli distribution Binomial distribution Exponential distribution Normal distribution Pareto distribution Poisson distribution Probability measure Random variable Bernoulli process Continuous or discrete Expected value Variance Markov chain Observed value Random walk Stochastic process
Complementary event Joint probability Marginal probability Conditional probability
Independence Conditional independence Law of total probability Law of large numbers Bayes' theorem Boole's inequality
Venn diagram Tree diagram
v t e

In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment.^[1][2] It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events (subsets of the sample space).^[3]

For instance, if X is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of X would take the value 0.5 (1 in 2 or 1/2) for X = heads, and 0.5 for X = tails (assuming that the coin is fair). More commonly, probability distributions are used to compare the relative occurrence of many different random values.

Probability distributions can be defined in different ways and for discrete or for continuous variables. Distributions with special properties or for especially important applications are given specific names.

Introduction

A probability distribution is a mathematical description of the probabilities of events, subsets of the sample space. The sample space, often represented in notation by ${\displaystyle \ \Omega \ ,}$ is the set of all possible outcomes of a random phenomenon being observed; it may be any set: A set of real numbers, a set of descriptive labels, a set of vectors, a set of arbitrary non-numerical values, etc. For example, the sample space of a coin flip would be  Ω = { "heads", "tails" } .

To define probability distributions for the specific case of random variables (so the sample space can be seen as a numeric set), it is common to distinguish between discrete and absolutely continuous random variables. In the discrete case, it is sufficient to specify a probability mass function ${\displaystyle \ p\ }$ assigning a probability to each possible outcome: for example, when throwing a fair dice, each of the six digits “1” to “6”, corresponding to the number of dots on the die, has the probability ${\displaystyle \ {\tfrac {1}{6}}~.}$ The probability of an event is then defined to be the sum of the probabilities of all outcomes that satisfy the event; for example, the probability of the event "the die rolls an even value" is

$${\displaystyle \ p({\text{“}}2{\text{”}})+p({\text{“}}4{\text{”}})+p({\text{“}}6{\text{”}})={\tfrac {1}{6}}+{\tfrac {1}{6}}+{\tfrac {1}{6}}={\tfrac {1}{2}}~.}$$

In contrast, when a random variable takes values from a continuum then by convention, any individual outcome is assigned probability zero. For such continuous random variables, only events that include infinitely many outcomes such as intervals have probability greater than 0.

For example, consider measuring the weight of a piece of ham in the supermarket, and assume the scale can provide arbitrarily many digits of precision. Then, the probability that it weighs exactly 500g must be zero because no matter how high the level of precision chosen, it cannot be assumed the there are no non-zero decimal digits in the remaining omitted digits ignored by the precision level.

However, for the same use case, it is possible to meet quality control requirements such as that a package of "500 g" of ham must weigh between 490 g and 510 g with at least 98% probability. This is possible because this measurement does not require as much precision from the underlying equipment.

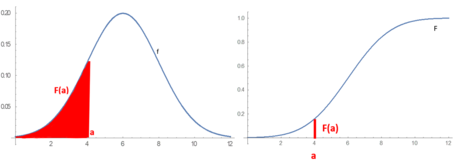
Absolutely continuous probability distributions can be described in several ways. The probability density function describes the infinitesimal probability of any given value, and the probability that the outcome lies in a given interval can be computed by integrating the probability density function over that interval.^[4] An alternative description of the distribution is by means of the cumulative distribution function, which describes the probability that the random variable is no larger than a given value (i.e., ${\displaystyle \ {\boldsymbol {\mathcal {P}}}(X<x)\ }$ for some ${\displaystyle \ x\ }$). The cumulative distribution function is the area under the probability density function from ${\displaystyle \ -\infty \ }$ to ${\displaystyle \ x\ ,}$ as shown in figure 1.^[5]

General probability definition

A probability distribution can be described in various forms, such as by a probability mass function or a cumulative distribution function. One of the most general descriptions, which applies for absolutely continuous and discrete variables, is by means of a probability function ${\displaystyle P\colon {\mathcal {A}}\to \mathbb {R} }$ whose input space ${\displaystyle {\mathcal {A}}}$ is a σ-algebra, and gives a real number probability as its output, particularly, a number in ${\displaystyle \subseteq \mathbb {R} }$.

The probability function ${\displaystyle P}$ can take as argument subsets of the sample space itself, as in the coin toss example, where the function ${\displaystyle P}$ was defined so that P(heads) = 0.5 and P(tails) = 0.5. However, because of the widespread use of random variables, which transform the sample space into a set of numbers (e.g., ${\displaystyle \mathbb {R} }$, ${\displaystyle \mathbb {N} }$), it is more common to study probability distributions whose argument are subsets of these particular kinds of sets (number sets),^[6] and all probability distributions discussed in this article are of this type. It is common to denote as ${\displaystyle P(X\in E)}$ the probability that a certain value of the variable ${\displaystyle X}$ belongs to a certain event ${\displaystyle E}$.^[7][8]

The above probability function only characterizes a probability distribution if it satisfies all the Kolmogorov axioms, that is:

1. ${\displaystyle P(X\in E)\geq 0\;\forall E\in {\mathcal {A}}}$, so the probability is non-negative
2. ${\displaystyle P(X\in E)\leq 1\;\forall E\in {\mathcal {A}}}$Zdroj:https://en.wikipedia.org?pojem=Continuous_probability
   Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.

   ---