The Butterworth filter is a type of signal processing filter designed to have a frequency response that is as flat as possible in the passband. It is also referred to as a maximally flat magnitude filter. It was first described in 1930 by the British engineer and physicist Stephen Butterworth in his paper entitled "On the Theory of Filter Amplifiers".^[1]

Original paper

Butterworth had a reputation for solving very complex mathematical problems thought to be 'impossible'. At the time, filter design required a considerable amount of designer experience due to limitations of the theory then in use. The filter was not in common use for over 30 years after its publication. Butterworth stated that:

"An ideal electrical filter should not only completely reject the unwanted frequencies but should also have uniform sensitivity for the wanted frequencies".

Such an ideal filter cannot be achieved, but Butterworth showed that successively closer approximations were obtained with increasing numbers of filter elements of the right values. At the time, filters generated substantial ripple in the passband, and the choice of component values was highly interactive. Butterworth showed that a low-pass filter could be designed whose gain as a function of frequency (i.e. the magnitude of its frequency response) is:

${\displaystyle G(\omega )={\frac {1}{\sqrt {1+{\omega }^{2n}}}},}$

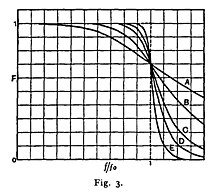
where ${\displaystyle \omega }$ is the angular frequency in radians per second and ${\displaystyle n}$ is the number of poles in the filter—equal to the number of reactive elements in a passive filter. Its cutoff frequency (the half-power point of approximately −3 dB or a voltage gain of 1/√2 ≈ 0.7071) is normalized to 𝜔 = 1 radian per second. Butterworth only dealt with filters with an even number of poles in his paper, though odd-order filters can be created with the addition of a single-pole filter applied to the output of the even-order filter. He built his higher-order filters from 2-pole filters separated by vacuum tube amplifiers. His plot of the frequency response of 2-, 4-, 6-, 8-, and 10-pole filters is shown as A, B, C, D, and E in his original graph.

Butterworth solved the equations for two-pole and four-pole filters, showing how the latter could be cascaded when separated by vacuum tube amplifiers and so enabling the construction of higher-order filters despite inductor losses. In 1930, low-loss core materials such as molypermalloy had not been discovered and air-cored audio inductors were rather lossy. Butterworth discovered that it was possible to adjust the component values of the filter to compensate for the winding resistance of the inductors.

He used coil forms of 1.25″ diameter and 3″ length with plug-in terminals. Associated capacitors and resistors were contained inside the wound coil form. The coil formed part of the plate load resistor. Two poles were used per vacuum tube and RC coupling was used to the grid of the following tube.

Butterworth also showed that the basic low-pass filter could be modified to give low-pass, high-pass, band-pass and band-stop functionality.

Overview

The frequency response of the Butterworth filter is maximally flat (i.e., has no ripples) in the passband and rolls off towards zero in the stopband.^[2] When viewed on a logarithmic Bode plot, the response slopes off linearly towards negative infinity. A first-order filter's response rolls off at −6 dB per octave (−20 dB per decade) (all first-order lowpass filters have the same normalized frequency response). A second-order filter decreases at −12 dB per octave, a third-order at −18 dB and so on. Butterworth filters have a monotonically changing magnitude function with ${\displaystyle \omega }$, unlike other filter types that have non-monotonic ripple in the passband and/or the stopband.

Compared with a Chebyshev Type I/Type II filter or an elliptic filter, the Butterworth filter has a slower roll-off, and thus will require a higher order to implement a particular stopband specification, but Butterworth filters have a more linear phase response in the passband than Chebyshev Type I/Type II and elliptic filters can achieve.

Example

A transfer function of a third-order low-pass Butterworth filter design shown in the figure on the right looks like this:

${\displaystyle {\frac {V_{o}(s)}{V_{i}(s)}}={\frac {R_{4}}{s^{3}(L_{1}C_{2}L_{3})+s^{2}(L_{1}C_{2}R_{4})+s(L_{1}+L_{3})+R_{4}}}}$

A simple example of a Butterworth filter is the third-order low-pass design shown in the figure on the right, with ${\displaystyle C_{2}}$ = 4/3 F, ${\displaystyle R_{4}}$ = 1 Ω, ${\displaystyle L_{1}}$ = 3/2 H, and ${\displaystyle L_{3}}$ = 1/2 H.^[3] Taking the impedance of the capacitors ${\displaystyle C}$ to be ${\displaystyle 1/(Cs)}$ and the impedance of the inductors ${\displaystyle L}$ to be ${\displaystyle Ls}$, where ${\displaystyle s=\sigma +j\omega }$ is the complex frequency, the circuit equations yield the transfer function for this device:

${\displaystyle H(s)={\frac {V_{o}(s)}{V_{i}(s)}}={\frac {1}{1+2s+2s^{2}+s^{3}}}.}$

The magnitude of the frequency response (gain) ${\displaystyle G(\omega )}$ is given by

${\displaystyle G(\omega )=|H(j\omega )|={\frac {1}{\sqrt {1+\omega ^{6}}}},}$

obtained from

${\displaystyle G^{2}(\omega )=|H(j\omega )|^{2}=H(j\omega )\cdot H^{*}(j\omega )={\frac {1}{1+\omega ^{6}}},}$

and the phase is given by

${\displaystyle \Phi (\omega )=\arg(H(j\omega )).\!}$

The group delay is defined as the negative derivative of the phase shift with respect to angular frequency and is a measure of the distortion in the signal introduced by phase differences for different frequencies. The gain and the delay for this filter are plotted in the graph on the left. It can be seen that there are no ripples in the gain curve in either the passband or the stop band.

The log of the absolute value of the transfer function ${\displaystyle H(s)}$ is plotted in complex frequency space in the second graph on the right. The function is defined by the three poles in the left half of the complex frequency plane.

These are arranged on a circle of radius unity, symmetrical about the real $$Zdroj:https://en.wikipedia.org?pojem=Butterworth_filter
Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.