In mathematics, a set B of vectors in a vector space V is called a basis (pl.: bases) if every element of V may be written in a unique way as a finite linear combination of elements of B. The coefficients of this linear combination are referred to as components or coordinates of the vector with respect to B. The elements of a basis are called basis vectors.

Equivalently, a set B is a basis if its elements are linearly independent and every element of V is a linear combination of elements of B.^[1] In other words, a basis is a linearly independent spanning set.

A vector space can have several bases; however all the bases have the same number of elements, called the dimension of the vector space.

This article deals mainly with finite-dimensional vector spaces. However, many of the principles are also valid for infinite-dimensional vector spaces.

Definition

A basis B of a vector space V over a field F (such as the real numbers R or the complex numbers C) is a linearly independent subset of V that spans V. This means that a subset B of V is a basis if it satisfies the two following conditions:

linear independence

for every finite subset ${\displaystyle \{\mathbf {v} _{1},\dotsc ,\mathbf {v} _{m}\}}$ of B, if ${\displaystyle c_{1}\mathbf {v} _{1}+\cdots +c_{m}\mathbf {v} _{m}=\mathbf {0} }$ for some ${\displaystyle c_{1},\dotsc ,c_{m}}$ in F, then ${\displaystyle c_{1}=\cdots =c_{m}=0}$;

spanning property

for every vector v in V, one can choose ${\displaystyle a_{1},\dotsc ,a_{n}}$ in F and ${\displaystyle \mathbf {v} _{1},\dotsc ,\mathbf {v} _{n}}$ in B such that ${\displaystyle \mathbf {v} =a_{1}\mathbf {v} _{1}+\cdots +a_{n}\mathbf {v} _{n}}$.

The scalars ${\displaystyle a_{i}}$ are called the coordinates of the vector v with respect to the basis B, and by the first property they are uniquely determined.

A vector space that has a finite basis is called finite-dimensional. In this case, the finite subset can be taken as B itself to check for linear independence in the above definition.

It is often convenient or even necessary to have an ordering on the basis vectors, for example, when discussing orientation, or when one considers the scalar coefficients of a vector with respect to a basis without referring explicitly to the basis elements. In this case, the ordering is necessary for associating each coefficient to the corresponding basis element. This ordering can be done by numbering the basis elements. In order to emphasize that an order has been chosen, one speaks of an ordered basis, which is therefore not simply an unstructured set, but a sequence, an indexed family, or similar; see § Ordered bases and coordinates below.

Examples

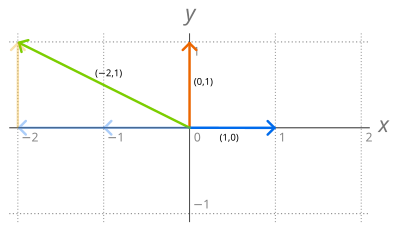
The set R² of the ordered pairs of real numbers is a vector space under the operations of component-wise addition

and scalar multiplication where ${\displaystyle \lambda }$ is any real number. A simple basis of this vector space consists of the two vectors e₁ = (1, 0) and e₂ = (0, 1). These vectors form a basis (called the standard basis) because any vector v = (a, b) of R² may be uniquely written as Any other pair of linearly independent vectors of R², such as (1, 1) and (−1, 2), forms also a basis of R².

More generally, if F is a field, the set ${\displaystyle F^{n}}$ of n-tuples of elements of F is a vector space for similarly defined addition and scalar multiplication. Let

be the n-tuple with all components equal to 0, except the ith, which is 1. Then ${\displaystyle \mathbf {e} _{1},\ldots ,\mathbf {e} _{n}}$ is a basis of ${\displaystyle F^{n},}$ which is called the standard basis of ${\displaystyle F^{n}.}$

A different flavor of example is given by polynomial rings. If F is a field, the collection F of all polynomials in one indeterminate X with coefficients in F is an F-vector space. One basis for this space is the monomial basis B, consisting of all monomials:

Any set of polynomials such that there is exactly one polynomial of each degree (such as the Bernstein basis polynomials or Chebyshev polynomials) is also a basis. (Such a set of polynomials is called a polynomial sequence.) But there are also many bases for F that are not of this form.

Properties

Many properties of finite bases result from the Steinitz exchange lemma, which states that, for any vector space V, given a finite spanning set S and a linearly independent set L of n elements of V, one may replace n well-chosen elements of S by the elements of L to get a spanning set containing L, having its other elements in S, and having the same number of elements as S.

Most properties resulting from the Steinitz exchange lemma remain true when there is no finite spanning set, but their proofs in the infinite case generally require the axiom of choice or a weaker form of it, such as the ultrafilter lemma.

If V is a vector space over a field F, then:

• If L is a linearly independent subset of a spanning set S ⊆ V, then there is a basis B such that
  $${\displaystyle L\subseteq B\subseteq S.}$$

  
• V has a basis (this is the preceding property with L being the empty set, and S = V).
• All bases of V have the same cardinality, which is called the dimension of V. This is the dimension theorem.
• A generating set S is a basis of V if and only if it is minimal, that is, no proper subset of S is also a generating set of V.
• A linearly independent set L is a basis if and only if it is maximal, that is, it is not a proper subset of any linearly independent set.

If V is a vector space of dimension n, then:

• A subset of V with n elements is a basis if and only if it is linearly independent.
• A subset of V with n elements is a basis if and only if it is a spanning set of V.

Coordinates

Let V be a vector space of finite dimension n over a field F, and

be a basis of V. By definition of a basis, every v in V may be written, in a unique way, as where the coefficients ${\displaystyle \lambda _{1},\ldots ,\lambda _{n}}$ are scalars (that is, elements of F), which are called the coordinates of v over B. However, if one talks of the set of the coefficients, one loses the correspondence between coefficients and basis elements, and several vectors may have the same set of coefficients. For example, ${\displaystyle 3\mathbf {b} _{1}+2\mathbf {b} _{2}}$ and ${\displaystyle 2\mathbf {b} _{1}+3\mathbf {b} _{2}}$ have the same set of coefficients {2, 3}, and are different. It is therefore often convenient to work with an ordered basis; this is typically done by indexing the basis elements by the first natural numbers. Then, the coordinates of a vector form a sequence similarly indexed, and a vector is completely characterized by the sequence of coordinates. An ordered basis is also called a frame, a word commonly used, in various contexts, for referring to a sequence of data allowing defining coordinates.

Let, as usual, ${\displaystyle F^{n}}$ be the set of the n-tuples of elements of F. This set is an F-vector space, with addition and scalar multiplication defined component-wise. The map