This article may require cleanup to meet Wikipedia's quality standards. The specific problem is: Excessive explanatory footnotes, some of which include other explanatory footnotes, which include other explanatory footnotes, and so on. Linearize by trimming for brevity, inserting into main text, or spawning subarticle(s). Please help improve this article if you can. (March 2024) (Learn how and when to remove this message)

24-cell
Schlegel diagram (vertices and edges)
Type	Convex regular 4-polytope
Schläfli symbol	{3,4,3} r{3,3,4} = ${\displaystyle \left\{{\begin{array}{l}3\\3,4\end{array}}\right\}}$ {31,1,1} = ${\displaystyle \left\{{\begin{array}{l}3\\3\\3\end{array}}\right\}}$
Coxeter diagram	or or
Cells	24 {3,4}
Faces	96 {3}
Edges	96
Vertices	24
Vertex figure	Cube
Petrie polygon	dodecagon
Coxeter group	F4, , order 1152 B4, , order 384 D4, , order 192
Dual	Self-dual
Properties	convex, isogonal, isotoxal, isohedral
Uniform index	22

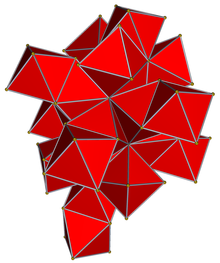
In four-dimensional geometry, the 24-cell is the convex regular 4-polytope^[1] (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,4,3}. It is also called C₂₄, or the icositetrachoron,^[2] octaplex (short for "octahedral complex"), icosatetrahedroid,^[3] octacube, hyper-diamond or polyoctahedron, being constructed of octahedral cells.

The boundary of the 24-cell is composed of 24 octahedral cells with six meeting at each vertex, and three at each edge. Together they have 96 triangular faces, 96 edges, and 24 vertices. The vertex figure is a cube. The 24-cell is self-dual.^[a] The 24-cell and the tesseract are the only convex regular 4-polytopes in which the edge length equals the radius.^[b]

The 24-cell does not have a regular analogue in 3 dimensions. It is the only one of the six convex regular 4-polytopes which is not the four-dimensional analogue of one of the five regular Platonic solids. It is the unique regular polytope, in any number of dimensions, which has no regular analogue in the adjacent dimension, either below or above.^[4] However, it can be seen as the analogue of a pair of irregular solids: the cuboctahedron and its dual the rhombic dodecahedron.^[5]

Translated copies of the 24-cell can tile four-dimensional space face-to-face, forming the 24-cell honeycomb. As a polytope that can tile by translation, the 24-cell is an example of a parallelotope, the simplest one that is not also a zonotope.^[6]

Geometry

The 24-cell incorporates the geometries of every convex regular polytope in the first four dimensions, except the 5-cell, those with a 5 in their Schlӓfli symbol,^[c] and the regular polygons with 7 or more sides. It is especially useful to explore the 24-cell, because one can see the geometric relationships among all of these regular polytopes in a single 24-cell or its honeycomb.

The 24-cell is the fourth in the sequence of 6 convex regular 4-polytopes (in order of size and complexity).^[d] It can be deconstructed into 3 overlapping instances of its predecessor the tesseract (8-cell), as the 8-cell can be deconstructed into 2 overlapping instances of its predecessor the 16-cell.^[8] The reverse procedure to construct each of these from an instance of its predecessor preserves the radius of the predecessor, but generally produces a successor with a smaller edge length.^[e]

Coordinates

Squares

The 24-cell is the convex hull of its vertices which can be described as the 24 coordinate permutations of:

$${\displaystyle (\pm 1,\pm 1,0,0)\in \mathbb {R} ^{4}.}$$

Those coordinates^[9] can be constructed as , rectifying the 16-cell with 8 vertices permutations of (±2,0,0,0). The vertex figure of a 16-cell is the octahedron; thus, cutting the vertices of the 16-cell at the midpoint of its incident edges produces 8 octahedral cells. This process^[10] also rectifies the tetrahedral cells of the 16-cell which become 16 octahedra, giving the 24-cell 24 octahedral cells.

In this frame of reference the 24-cell has edges of length √2 and is inscribed in a 3-sphere of radius √2. Remarkably, the edge length equals the circumradius, as in the hexagon, or the cuboctahedron. Such polytopes are radially equilateral.^[b]

Regular convex 4-polytopes of radius √2
Symmetry group	A4	B4		F4	H4
Name	5-cell Hyper-tetrahedron 5-point	16-cell Hyper-octahedron 8-point	8-cell Hyper-cube 16-point	24-cell 24-point	600-cell Hyper-icosahedron 120-point	120-cell Hyper-dodecahedron 600-point
Schläfli symbol	{3, 3, 3}	{3, 3, 4}	{4, 3, 3}	{3, 4, 3}	{3, 3, 5}	{5, 3, 3}
Coxeter mirrors
Mirror dihedrals	𝝅/3 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2	𝝅/3 𝝅/3 𝝅/4 𝝅/2 𝝅/2 𝝅/2	𝝅/4 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2	𝝅/3 𝝅/4 𝝅/3 𝝅/2 𝝅/2 𝝅/2	𝝅/3 𝝅/3 𝝅/5 𝝅/2 𝝅/2 𝝅/2	𝝅/5 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2
Graph
Vertices	5 tetrahedral	8 octahedral	16 tetrahedral	24 cubical Zdroj:https://en.wikipedia.org?pojem=24-cell Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia.  Navigácia: Veda > Analytika Antropológia Aplikované vedy Bibliometria Dejiny vedy Encyklopédie Filozofia vedy Forenzné vedy Humanitné vedy Knižničná veda Kryogenika Kryptológia Kulturológia Literárna veda Medzidisciplinárne oblasti Metódy kvantitatívnej analýzy Metavedy Metodika Metodológia vedy Náboženstvo a veda Náučná literatúra Podvody vo vede Popularizácia vedy Potravinárstvo Prírodné vedy Pseudoveda Scientometria Spoločenské vedy Teórie Teatrológia Technické vedy Technika Terminológia Umenie Výskum Veda Veda a technika podľa štátu Veda a technika podľa kontinentu Veda a technika podľa roka Veda v kozme Vedci Vedecká literatúra Vedecké databázy Vedecké experimenty Vedecké konferencie Vedecké metódy Vedecké ocenenia Vedecké organizácie Vedecké parky Vedeckí spisovatelia Vzdelávanie Záhady Príbuzné výrazy: Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia. www.astronomia.sk | www.biologia.sk | www.botanika.sk | www.dejiny.sk | www.economy.sk | www.elektrotechnika.sk | www.estetika.sk | www.farmakologia.sk | www.filozofia.sk | Fyzika | www.futurologia.sk | www.genetika.sk | www.chemia.sk | www.lingvistika.sk | www.politologia.sk | www.psychologia.sk | www.sexuologia.sk | www.sociologia.sk | www.veda.sk I www.zoologia.sk